八年级（上）期末数学试卷集（305题）

---

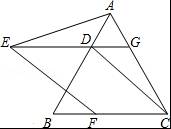
已知：如图，△ABC为等边三角形，过AB边上的点D作DG∥BC，交AC于G，在GD的延长线上取点E，使DE=DB，连接AE，CD．

（1）求证：△AGE≌△DAC；

（2）把线段DC沿DE方向向左平移，当D平移至点E的位置时，点C恰好与线段BC上的点F重合（如图），请连接AF，并判断△AEF是怎样的三角形，试证明你的结论．

知识点：试卷09

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等边三角形的性质；平移的性质．

【分析】（1）根据已知等边三角形的性质可推出△ADG是等边三角形，从而再利用SAS判定△AGE≌△DAC；

（2）连接AF，由已知可得四边形EFCD是平行四边形，从而得到EF=CD，∠DEF=∠DCF，由（1）知△AGE≌△DAC得到AE=CD，∠AED=∠ACD，从而可得到EF=AE，∠AEF=60°，所以△AEF为等边三角形．

【解答】（1）证明：∵△ABC是等边三角形，

∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°．

∵EG∥BC，

∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°．

∴△ADG是等边三角形．

∴AD=DG=AG．

∵DE=DB，

∴EG=AB．

∴GE=AC．

∵EG=AB=CA，

∴∠AGE=∠DAC=60°，

在△AGE和△DAC中，

，

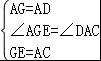∴△AGE≌△DAC（SAS）．

（2）解：△AEF为等边三角形．

证明：如图，连接AF，

∵DG∥BC，EF∥DC，

∴四边形EFCD是平行四边形，

∴EF=CD，∠DEF=∠DCF，

由（1）知△AGE≌△DAC，

∴AE=CD，∠AED=∠ACD．

∵EF=CD=AE，∠AED+∠DEF=∠ACD+∠DCB=60°，

∴△AEF为等边三角形．