第261题

如图．△ABC中，AB=AC，AB的垂直平分线交AC于P点，若AB=6cm，BC=4cm，△PBC的周长等于（　　）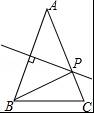

A.4cm

B.6cm

C.8cm

D.10cm

参考答案：D

解析：

【考点】线段垂直平分线的性质；等腰三角形的性质．

【分析】先根据等腰三角形的性质得出AC=AB=6cm，再根据线段垂直平分线的性质得出AP=BP，故AP+PC=AC，由此即可得出结论．

【解答】解：∵△ABC中，AB=AC，AB=6cm，

∴AC=6cm，

∵AB的垂直平分线交AC于P点，

∴BP+PC=AC，

∴△PBC的周长=（BP+PC）+BC=AC+BC=6+4=10cm．

故选：D．

第262题

如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（　　）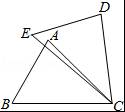

A.BC=EC，∠B=∠E

B.BC=EC，AC=DC

C.BC=DC，∠A=∠D

D.∠B=∠E，∠A=∠D

参考答案：C

解析：

【考点】全等三角形的判定．

【分析】根据全等三角形的判定方法分别进行判定即可．

【解答】解：A、已知AB=DE，再加上条件BC=EC，∠B=∠E可利用SAS证明△ABC≌△DEC，故此选项不合题意；

B、已知AB=DE，再加上条件BC=EC，AC=DC可利用SSS证明△ABC≌△DEC，故此选项不合题意；

C、已知AB=DE，再加上条件BC=DC，∠A=∠D不能证明△ABC≌△DEC，故此选项符合题意；

D、已知AB=DE，再加上条件∠B=∠E，∠A=∠D可利用ASA证明△ABC≌△DEC，故此选项不合题意；

故选：C．

第263题

如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（　　）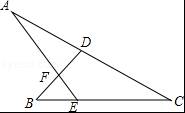

A.110°

B.115°

C.120°

D.125°

参考答案：A

解析：

【考点】三角形的外角性质；三角形内角和定理．

【分析】根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°，∠DFE=∠B+∠AEC，进而可得答案．

【解答】解：∵∠A=27°，∠C=38°，

∴∠AEB=∠A+∠C=65°，

∵∠B=45°，

∴∠DFE=65°+45°=110°，

故选A．

第264题

分解因式：a³﹣a=　　．

参考答案：a（a+1）（a﹣1）

解析：

【考点】提公因式法与公式法的综合运用．

【分析】先提取公因式a，再对余下的多项式利用平方差公式继续分解．

【解答】解：a³﹣a，

=a（a²﹣1），

=a（a+1）（a﹣1）．

故答案为：a（a+1）（a﹣1）．

第265题

3^﹣2=　　；0.0000000251=　　（用科学记数法表示）

参考答案：1/9，2.51×10^﹣8

解析：

【考点】科学记数法—表示较小的数．

【分析】根据负整数指数幂与正整数指数幂互为倒数，可得答案；

绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10^﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【解答】解：3^﹣2==；0.0000000251=2.51×10^﹣8（用科学记数法表示），

故答案为：，2.51×10^﹣8．

第266题

点M（3，﹣4）关于x轴的对称点的坐标是　　．

参考答案：（3，4）

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．

【解答】解：点M（3，﹣4）关于x轴的对称点M′的坐标是（3，4）．

故答案为：（3，4）．

第267题

如图，AD是等边三角形ABC的中线，AE=AD，则∠EDC=　　．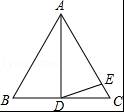

参考答案：15°

解析：

【考点】等边三角形的性质．

【分析】由AD是等边△ABC的中线，根据等边三角形中：三线合一的性质，即可求得AD⊥BC，∠CAD=30°，又由AD=AE，根据等边对等角与三角形内角和定理，即可求得∠ADE的度数，继而求得答案．

【解答】解：∵AD是等边△ABC的中线，

∴AD⊥BC，∠BAD=∠CAD=∠BAC=×60°=30°，

∴∠ADC=90°，

∵AD=AE，

∴∠ADE=∠AED==75°，

∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°．

故答案为：15°．

第268题

如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD=　　．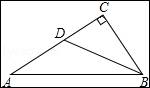

参考答案：3

解析：

【考点】含30度角的直角三角形．

【分析】由于∠C=90°，∠ABC=60°，可以得到∠A=30°，又由BD平分∠ABC，可以推出∠CBD=∠ABD=∠A=30°，∴BD=AD=6，再由30°角所对的直角边等于斜边的一半即可求出结果．

【解答】解：∵∠C=90°，∠ABC=60°，

∴∠A=30°，

∵BD平分∠ABC，

∴∠CBD=∠ABD=∠A=30°，

∴BD=AD=6，

∴CD=BD=6×=3．

故答案为：3．

第269题

x²+kx+9是完全平方式，则k=　　．

参考答案：±6

解析：

【考点】完全平方式．

【分析】这里首末两项是x和3这两个数的平方，那么中间一项为加上或减去x和3的积的2倍，故k=±6．

【解答】解：中间一项为加上或减去x和3的积的2倍，

故k=±6．

第270题

如图在等腰Rt△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于D，DE⊥AB于E，若AB=10，则△BDE的周长等于　　．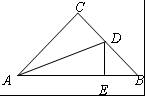

参考答案：10

解析：

【考点】角平分线的性质；等腰直角三角形．

【分析】由题中条件可得Rt△ACD≌Rt△AED，进而得出AC=AE，AC=AE，把△BDE的边长通过等量转化即可得出结论．

【解答】解：∵AD平分∠CAB，AC⊥BC于点C，DE⊥AB于E，∴CD=DE．

又∵AD=AD，

∴Rt△ACD≌Rt△AED，∴AC=AE．

又∵AC=BC，

∴BC=AE，

∴△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=10．

（提示：设法将DE+BD+EB转成线段AB）．

故答案为：10．

第271题

如图，已知∠MON=30°，点A₁，A₂，A₃，…在射线ON上，点B₁，B₂，B₃，…在射线OM上，△A₁B₁A₂，△A₂B₂A₃，△A₃B₃A₄，…均为等边三角形，若OA₁=2，则△A₅B₅A₆的边长为　　．

参考答案：32

解析：

【考点】等边三角形的性质．

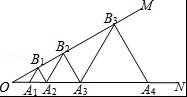
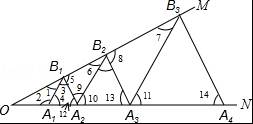
【分析】根据等腰三角形的性质以及平行线的性质得出A₁B₁∥A₂B₂∥A₃B₃，以及A₂B₂=2B₁A₂，得出A₃B₃=4B₁A₂=4，A₄B₄=8B₁A₂=8，A₅B₅=16B₁A₂…进而得出答案．

【解答】解：∵△A₁B₁A₂是等边三角形，

∴A₁B₁=A₂B₁，∠3=∠4=∠12=60°，

∴∠2=120°，

∵∠MON=30°，

∴∠1=180°﹣120°﹣30°=30°，

又∵∠3=60°，

∴∠5=180°﹣60°﹣30°=90°，

∵∠MON=∠1=30°，

∴OA₁=A₁B₁=2，

∴A₂B₁=2，

∵△A₂B₂A₃、△A₃B₃A₄是等边三角形，

∴∠11=∠10=60°，∠13=60°，

∵∠4=∠12=60°，

∴A₁B₁∥A₂B₂∥A₃B₃，B₁A₂∥B₂A₃，

∴∠1=∠6=∠7=30°，∠5=∠8=90°，

∴A₂B₂=2B₁A₂，B₃A₃=2B₂A₃，

∴A₃B₃=4B₁A₂=4，

A₄B₄=8B₁A₂=8，

A₅B₅=16B₁A₂=16，

以此类推：A₆B₆=32B₁A₂=32．

故答案是：32．

第272题

化简：（x+y）（x﹣y）﹣（2x﹣y）（x+3y）

参考答案：见解析

解析：

【考点】平方差公式；多项式乘多项式．

【分析】根据整式运算的法则即可求出答案．

【解答】解：原式=x²﹣y²﹣（2x²+6xy﹣xy﹣3y²）

=x²﹣y²﹣2x²﹣5xy+3y²

=﹣x²﹣5xy+2y²

第273题

先化简，（﹣）÷，再选一个合适的数作为a的值计算．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】首先把除法转化为乘法，利用分配律计算，然后合并同类项即可化简，然后代入使分式有意义的a的值求解．

【解答】解：原式=（﹣）•（a+1）（a﹣1）

=2a（a+1）﹣a（a﹣1）

=2a²+2a﹣a2+a

=a²+3a．

当a=0时，原式=0．

第274题

如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．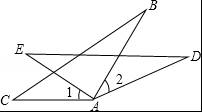

参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【分析】先证出∠CAB=∠DAE，再由SAS证明△BAC≌△DAE，得出对应边相等即可．

【解答】证明：∵∠1=∠2，

∴∠CAB=∠DAE，

在△BAC和△DAE中，，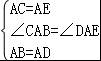

∴△BAC≌△DAE（SAS），

∴BC=DE．

第275题

如图，△ABC中，A点坐标为（2，4），B点坐标为（﹣3，﹣2），C点坐标为（3，1）．

（1）在图中画出△ABC关于y轴对称的△A′B′C′（不写画法），并写出点A′，B′，C′的坐标．

参考答案：见解析

解析：

【考点】作图-轴对称变换．

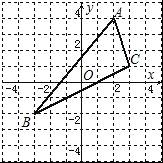
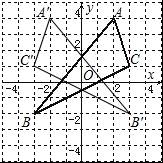
【分析】（1）根据网格结构找出点A′、B′、C′的位置，然后顺次连接即可；

（2）利用三角形所在的矩形的面积减去四周三个小直角三角形的面积，然后列式计算即可得解．

【解答】解：（1）如图，A′（﹣2，4），B′（3，﹣2），C′（﹣3，1）；

（2）S_△ABC=6×6﹣×5×6﹣×6×3﹣×1×3，

=36﹣15﹣9﹣1，

=10．

第276题

小明和小张两人练习电脑打字，小明每分钟比小张少打6个字，小明打120个字所用的时间和小张打180个字所用的时间相等．求小明和小张每分钟各打多少个字？

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】首先设小明每分钟打x个字，则小张每分钟打（x+6）个字，根据小明打120个字所用的时间和小张打180个字所用的时间相等列出方程，再解即可．

【解答】解：设小明每分钟打x个字，则小张每分钟打（x+6）个字，

根据题意，得=，

解得：x=12，

经检验：x=12是原分式方程的解，

12+6=18（个），

答：小明和小张每分钟各打12个和18个字．

第277题

已知：如图，E、F在AC上，AD∥CB且AD=CB，∠D=∠B．求证：AE=CF．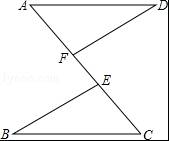

参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【分析】根据两直线平行内错角相等即可得出∠A=∠C，再根据全等三角形的判定即可判断出△ADF≌△CBE，得出AF=CE，进而得出AE=CF．

【解答】证明：∵AD∥CB，

∴∠A=∠C，

在△ADF和△CBE中，

，

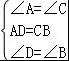∴△ADF≌△CBE（ASA），

∴AF=CE，

∴AF+EF=CE+EF，即AE=CF．

第278题

已知：如图，在△ABC中，∠C=90°，AE是△ABC的角平分线；ED平分∠AEB，交AB于点D；∠CAE=∠B．

（1）求∠B的度数．

参考答案：见解析

解析：

【考点】角平分线的性质；含30度角的直角三角形．

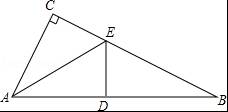
【分析】（1）先由角平分线的定义及已知条件得出∠CAE=∠EAB=∠B，再根据直角三角形两锐角互余得出∠CAE+∠EAB+∠B=3∠B=90°，那么∠B=30°；

（2）根据30°角所对的直角边等于斜边的一半得出AB=2AC=6cm；

（3）先由∠EAB=∠B，根据等角对等边得出EB=EA，又ED平分∠AEB，根据等腰三角形三线合一的性质得到ED⊥AB．

【解答】解：（1）∵AE是△ABC的角平分线，

∴∠CAE=∠EAB，

∵∠CAE=∠B，

∴∠CAE=∠EAB=∠B．

∵在△ABC中，∠C=90°，

∴∠CAE+∠EAB+∠B=3∠B=90°，

∴∠B=30°；

（2）∵在△ABC中，∠C=90°，∠B=30°，AC=3cm，

∴AB=2AC=6cm；

（3）猜想：ED⊥AB．理由如下：

∵∠EAB=∠B，

∴EB=EA，

∵ED平分∠AEB，

∴ED⊥AB．

第279题

乘法公式的探究与应用：

参考答案：见解析

解析：

【考点】平方差公式的几何背景．

【分析】（1）中的面积=大正方形的面积﹣小正方形的面积=a²﹣b²；

（2）中的长方形，宽为a﹣b，长为a+b，面积=长×宽=（a+b）（a﹣b）；

（3）中的答案可以由（1）、（2）得到（a+b）（a﹣b）=a²﹣b²；反过来也成立；

（4）把10.3×9.7写成（10+0.3）（10﹣0.3），利用公式求解即可．

【解答】解：（1）阴影部分的面积=大正方形的面积﹣小正方形的面积=a²﹣b²；

（2）长方形的宽为a﹣b，长为a+b，面积=长×宽=（a+b）（a﹣b）；

故答案为：a+b，a﹣b，（a+b）（a﹣b）；

（3）由（1）、（2）得到，公式1：（a+b）（a﹣b）=a²﹣b²；

公式2：a²﹣b²=（a+b）（a﹣b）

故答案为：（a+b）（a﹣b），a²﹣b²=（a+b）（a﹣b）；

（4）10.3×9.7=（10+0.3）（10﹣0.3）

=10²﹣0.3²

=100﹣0.09

=99.91．

第280题

要使分式x－3(x－1)有意义，x的取值应满足(　　)

A.x＝1

B.x≠1

C.x＝3

D.x≠3

参考答案：D