第161题

如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S_△ABD：S_△ACD=（　　）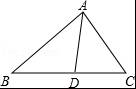

A.3：4

B.4：3

C.16：9

D.9：16

参考答案：B

解析：

【考点】三角形的面积．

【分析】利用角平分线的性质，可得出△ABD的边AB上的高与△ACD的AC上的高相等，估计三角形的面积公式，即可得出△ABD与△ACD的面积之比等于对应边之比．

【解答】解：∵AD是△ABC的角平分线，

∴设△ABD的边AB上的高与△ACD的AC上的高分别为h₁，h₂，

∴h₁=h₂，

∴△ABD与△ACD的面积之比=AB：AC=8：6=4：3，

故选：B．

第162题

已知△A₁B₁C₁，△A₂B₂C₂的周长相等，现有两个判断：

①若A₁B₁=A₂B₂，A₁C₁=A₂C₂，则△A₁B₁C₁≌△A₂B₂C₂；

A.①正确，②错误

B.①错误，②正确

C.①，②都错误

D.①，②都正确

参考答案：D

解析：

【考点】全等三角形的判定．

【分析】根据SSS即可推出△A₁B₁C₁≌△A₂B₂C₂，判断①正确；根据“两角法”推知两个三角形相似，然后结合两个三角形的周长相等推出两三角形全等，即可判断②．

【解答】解：∵△A₁B₁C₁，△A₂B₂C₂的周长相等，A₁B₁=A₂B₂，A₁C₁=A₂C₂，

∴B₁C₁=B₂C₂，

∴△A₁B₁C₁≌△A₂B₂C₂（SSS），∴①正确；

∵∠A₁=∠A₂，∠B₁=∠B₂，

∴△A₁B₁C₁∽△A₂B₂C₂

∵△A₁B₁C₁，△A₂B₂C₂的周长相等，

∴△A₁B₁C₁≌△A₂B₂C₂

∴②正确；

故选：D．

第163题

因式分解：x³﹣4xy²=　　．

参考答案：x（x+2y）（x﹣2y）

解析：

【考点】提公因式法与公式法的综合运用．

【分析】先提公因式x，再利用平方差公式继续分解因式．

【解答】解：x³﹣4xy²，

=x（x²﹣4y²），

=x（x+2y）（x﹣2y）．

第164题

已知△ABC为等腰三角形，①当它的两个边长分别为8cm和3cm时，它的周长为　　；②如果它的一边长为4cm，一边的长为6cm，则周长为　　．

参考答案：19cm，14cm或16cm

解析：

【考点】等腰三角形的性质；三角形三边关系．

【分析】题目给出等腰三角形有两条边长，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．

【解答】解：①当腰长为8cm时，三边是8cm，8cm，3cm，符合三角形的三边关系，此时周长是19cm；

当腰长为3cm时，三角形的三边是8cm，3cm，3cm，因为3+3＜8，应舍去．

②当腰长为4cm时，三角形的三边是4cm，4cm，6cm，符合三角形的三边关系，此时周长是14cm；

当腰长为6cm时，三角形的三边是6cm，6cm，4cm，符合三角形的三边关系，此时周长是16cm．

故答案为：19cm，14cm或16cm．

第165题

如图，BC=EC，∠1=∠2，添加一个适当的条件使△ABC≌△DEC，则需添加的条件是　　（不添加任何辅助线）．

参考答案：∠A=∠D

解析：

【考点】全等三角形的判定．

【分析】先求出∠ACB=∠DCE，再添加∠A=∠D，由已知条件BC=EC，即可证明△ABC≌△DEC．

【解答】解：添加条件：∠A=∠D；

∵∠1=∠2，

∴∠1+∠ECA=∠2+∠ECA，

即∠ACB=∠DCE，

在△ABC和△DEC中，

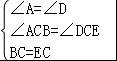
∴△ABC≌△DEC（AAS）．

第166题

若分式的值为0，则m的值为　　．

参考答案：3

解析：

【考点】分式的值为零的条件．

【分析】直接利用分式的值为零，则分子为零，且分母不为零，进而得出答案．

【解答】解：由题意，得

m²﹣9=0且m+3≠0，

解得m=3，

故答案为：3．

第167题

若关于x的方程无解．则m=　　．

参考答案：3

解析：

【考点】分式方程的解．

【分析】关于x的分式方程无解，即分式方程去掉分母化为整式方程，整式方程的解就是方程的增根，即x=3，据此即可求解．

【解答】解：去分母得：x﹣2（x﹣3）=m

解得：x=6﹣m

根据题意得：6﹣m=3

解得：m=3

故答案是：3．

第168题

如图，△ABC的周长为19cm，AC的垂直平分线DE交BC于D，E为垂足，AE=3cm，则△ABD的周长为　　cm．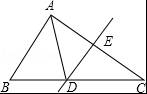

参考答案：13

解析：

【考点】线段垂直平分线的性质．

【分析】根据垂直平分线的性质计算．

△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC

【解答】解：∵AC的垂直平分线DE交BC于D，E为垂足

∴AD=DC，AC=2AE=6cm，

∵△ABC的周长为19cm，

∴AB+BC=13cm

∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm．

故填13．

第169题

因式分解．

（1）2x³﹣4x²+2x

参考答案：见解析

解析：

【考点】提公因式法与公式法的综合运用．

【分析】

（1）首先提公因式2x，再利用完全平方公式进行分解即可；

（2）首先提公因式x，再利用平方差公式进行分解即可．

【解答】

解：（1）原式=2x（x²﹣2x+1）=2x（x﹣1）²；

（2）原式=x（x²﹣9y²）=x（x﹣3y）（x+3y）．

第170题

解下列方程

（1）；

参考答案：见解析

解析：

【考点】解分式方程．

【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

【解答】（1）解：两边同乘x﹣2，得：3+x=﹣2（x﹣2），

去括号得：3+x=﹣2x+4，

移项合并得：3x=1，

解得：x=，

经检验，x=是原方程的解；

（2）两边同乘（x﹣1）（x+1），得：（x+1）²﹣4=x²﹣1，

去括号得：x²+2x+1﹣4=x²﹣1，

移项合并得：2x=2，

解得：x=1，

经检验，x=1是原方程的增根，

则原方程无解．

第171题

先化简，再求值：（﹣）÷，其中x=﹣1．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．

【解答】解：原式=[﹣]÷

=[﹣]÷

=÷

=×

=

当x=﹣1时，原式=．

第172题

在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，﹣1）．

（1）将△ABC沿y轴正方向平移3个单位得到△A₁B₁C₁，画出△A₁B₁C₁，并写出点B₁坐标；

参考答案：见解析

解析：

【考点】作图-轴对称变换；作图-平移变换．

【分析】（1）直接利用平移的性质得出平移后对应点位置进而得出答案；

（2）利用轴对称图形的性质得出对应点位置进而得出答案．

【解答】解：（1）如图所示：△A₁B₁C₁，即为所求；点B₁坐标为：（﹣2，﹣1）；

（2）如图所示：△A₂B₂C₂，即为所求，点C₂的坐标为：（1，1）．

第173题

从甲市到乙市乘坐高速列车的路程为180千米，乘坐普通列车的路程为240千米．高速列车的平均速度是普通列车的平均速度的3倍．高速列车的乘车时间比普通列车的乘车时间缩短了2小时．高速列车的平均速度是每小时多少千米？

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】设普通列车平均速度每小时x千米，则高速列车平均速度每小时3x千米，根据题意可得，坐高铁走180千米比坐普通车240千米少用2小时，据此列方程求解．

【解答】解：设普通列车平均速度每小时x千米，则高速列车平均速度每小时3x千米，

根据题意得，﹣=2，

解得：x=90，

经检验，x=90是所列方程的根，

则3x=3×90=270．

答：高速列车平均速度为每小时270千米．

第174题

如图，在△ABC中，已知∠ABC=46°，∠ACB=80°，延长BC至D，使CD=CA，连接AD，求∠BAD的度数．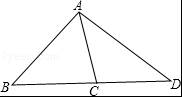

参考答案：见解析

解析：

【考点】三角形内角和定理；三角形的外角性质；等腰三角形的性质．

【分析】要求∠BAD的度数，只要求出∠C的度数就行了，根据三角形内角和为180°，求出∠BAD的度数，根据三角形内角和外角关系及等腰三角形性质，易求∠C的度数．

【解答】解：∵∠ACB=80°

∴∠ACD=180°﹣∠ACB=180°﹣80°=100°

又∵CD=CA

∴∠CAD=∠D

∵∠ACD+∠CAD+∠D=180°

∴∠CAD=∠D=40°

在△ABC内

∴∠BAD=180°﹣∠ABC﹣∠D=180°﹣46°﹣40°=94°．

第175题

如图，BF⊥AC，CE⊥AB，BE=CF，BF、CE交于点D，求证：AD平分∠BAC．

参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【分析】先由条件可以得出△BED≌△CFD就有DE=DF，就可以得出结论．

【解答】证明：∵BF⊥AC，CE⊥AB，

∴∠BED=∠CFD=90°．

在△BED和△CFD中，

，

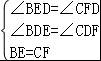∴△BED≌△CFD（AAS），

∴DE=DF．

∵DF⊥AC，DE⊥AB，

∴AD平分∠BAC．

第176题

如图，正方形ABCD的边长为1，G为CD边上一动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．

求证：①△BCG≌△DCE；②BH⊥DE．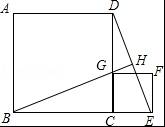

参考答案：见解析

解析：

【考点】正方形的性质；全等三角形的判定与性质．

【分析】（1）根据正方形的边的性质和直角可通过SAS判定△BCG≌△DCE，

（2）利用全等的性质得到∠BHD=90°即BH⊥DE．

【解答】证明：（1）在正方形ABCD中，∠BCG=90°，BC=CD

在正方形GCEF中，∠DCE=90°，CG=CE

在△BCG和△DCE中，

，

∴△BCG≌△DCE（SAS）

（2）∵△BCG≌△DCE，

∴∠1=∠2，

∵∠2+∠DEC=90°

∴∠1+∠DEC=90°

∴∠BHD=90°

∴BH⊥DE；

第177题

式子有意义的条件是（　　）

A.x≥3

B.x＞3

C.x≥﹣3

D.x＞﹣3

参考答案：C

解析：

【考点】二次根式有意义的条件．

【分析】根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可．

【解答】解：由题意得，x+3≥0，

解得，x≥﹣3，

故选：C．

【点评】本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题的关键．

第178题

下列平面图形中，不是轴对称图形的是（　　）

A.

B.

C.

D.

参考答案：A

解析：

【考点】轴对称图形．

【分析】根据轴对称图形的定义作答．

如果把一个图形沿着一条直线翻折过来，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．

【解答】解：根据轴对称图形的概念，可知只有A沿任意一条直线折叠直线两旁的部分都不能重合．

故选：A．

【点评】轴对称的关键是寻找对称轴，两边图象折叠后可重合

第179题

下列各式运算正确的是（　　）

A.

B.4

C.

D.

参考答案：D

解析：

【考点】二次根式的混合运算．

【分析】计算出各个选项中式子的正确结果，然后对照即可得到哪个选项是正确的．

【解答】解：∵，故选项A错误；

∵，故选项B错误；

∵，故选项C错误；

∵，故选项D正确；

故选D．

【点评】本题考查二次根式的混合运算，解题的关键是明确二次根式混合运算的计算方法．

第180题

一粒花粉的质量约为0.000037毫克，那么0.000037可用科学记数法表示为（　　）

A.3.7×10^﹣5

B.3.7×10^﹣6

C.37×10^﹣7

D.3.7×10^﹣8

参考答案：A

解析：

【考点】科学记数法—表示较小的数．

【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10^﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【解答】解：0.000037可用科学记数法表示为3.7×10^﹣5，

故选：A．

【点评】本题考查用科学记数法表示较小的数，一般形式为a×10^﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．