第141题

如图，有一块边长为4的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是　　．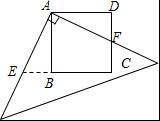

参考答案：16

解析：

【考点】正方形的性质；全等三角形的判定与性质．

【分析】由四边形ABCD为正方形可以得到∠D=∠B=90°，AD=AB，又∠ABE=∠D=90°，而∠EAF=90°由此可以推出∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，进一步得到∠DAF=∠BAE，所以可以证明△AEB≌△AFD，所以S_△AEB=S_△AFD，那么它们都加上四边形ABCF的面积，即可四边形AECF的面积=正方形的面积，从而求出其面积．

【解答】解：∵四边形ABCD为正方形，

∴∠D=∠ABC=90°，AD=AB，

∴∠ABE=∠D=90°，

∵∠EAF=90°，

∴∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，

∴∠DAF=∠BAE，

在△AEB和△AFD中，

∵，

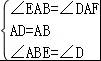∴△AEB≌△AFD（ASA），

∴S_△AEB=S_△AFD，

∴它们都加上四边形ABCF的面积，

可得到四边形AECF的面积=正方形的面积=16．

故答案为：16．

第142题

如图，AB+AC=7，D是AB上一点，若点D在BC的垂直平分线上，则△ACD的周长为　　．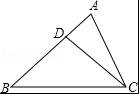

参考答案：7

解析：

【考点】线段垂直平分线的性质．

【分析】先根据点D在BC的垂直平分线上得出BD=CD，故△ACD的周长=AD+CD+AC=AD+BD+AC=AB+AC．

【解答】解：∵AB+AC=7，D是AB上一点，点D在BC的垂直平分线上，

∴BD=CD，

∴△ACD的周长=AD+CD+AC=AD+BD+AC=AB+AC=7．

故答案为：7．

第143题

如图，正方形ABCD中，截去∠A，∠C后，∠1，∠2，∠3，∠4的和为　　．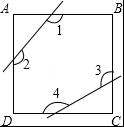

参考答案：540°

解析：

【考点】多边形内角与外角．

【分析】根据多边形内角和为（n﹣2）×180°，再根据正方形性质即可得出答案．

【解答】解：根据多边形内角和为（n﹣2）×180°，

∴截得的六边形的和为（6﹣2）×180°=720°，

∵∠B=∠C=90°，

∴∠1，∠2，∠3，∠4的和为720°﹣180°=540°．

故答案为540°．

第144题

化简﹣的结果是　　．

参考答案：m+3

解析：

【考点】分式的加减法．

【分析】根据同分母分式加减法法则，求出﹣的化简结果即可．

【解答】解：﹣

=

=

=m+3

故答案为：m+3．

第145题

计算：

（1）x（4x+3y）﹣（2x+y）（2x﹣y）

参考答案：见解析

解析：

【考点】分式的混合运算；整式的混合运算．

【分析】（1）根据整式的混合计算顺序计算即可；

（2）根据分式的混合计算顺序计算即可．

【解答】解：（1）原式=4x²+3xy﹣（4x²﹣y²）

=4x²+3xy﹣4x²+y²

=3xy+y²；

（2）原式=

=

=．

第146题

分解因式：（m﹣n）（3m+n）²+（m+3n）²（n﹣m）

参考答案：见解析

解析：

【考点】提公因式法与公式法的综合运用．

【分析】先提取公因式（m﹣n），再利用平方差公式进行二次分解即可求解．

【解答】解：（m﹣n）（3m+n）²+（m+3n）²（n﹣m）

=（m﹣n）[（3m+n）²﹣（m+3n）²]

=（m﹣n）（3m+n+m+3n）（3m+n﹣m﹣3n）

=8（m﹣n）²（m+n）．

第147题

解方程：

（1）+3=

参考答案：见解析

解析：

【考点】解分式方程．

【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

【解答】解：（1）去分母得：1+3x﹣6=x﹣1，

移项合并得：2x=4，

解得：x=2，

经检验x=2是增根，分式方程无解；

（2）去分母得：（x﹣2）²﹣12=x²﹣4，

整理得：x²﹣4x+4﹣12=x²﹣4，

移项合并得：﹣4x=4，

解得：x=﹣1，

经检验x=﹣1是分式方程的解．

第148题

如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑．请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．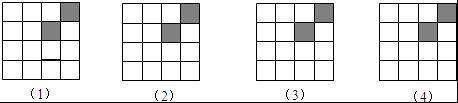

参考答案：见解析

解析：

【考点】利用轴对称设计图案．

【分析】根据轴对称图形的性质可知，正方形的轴对称图形，是四边的垂直平分线，所以可以先找到正方形的对称轴，再在对称图形中找到相同的部分就是轴对称图形．

【解答】解：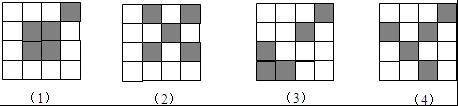

注：本题画法较多，只要满足题意均可，画对一个得．

第149题

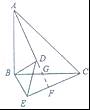
已知：如图，△ABC和△DBE均为等腰直角三角形．

（1）求证：AD=CE；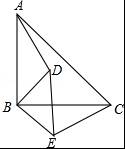

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等腰直角三角形．

【分析】（1）由等腰直角三角形的性质得出AB=BC，BD=BE，∠ABC=∠DBE=90°，得出∠ABD=CBE，证出△ABD≌△CBE（SAS），得出AD=CE；

（2）△ABD≌△CBE得出∠BAD=∠BCE，再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°，得出∠AFC=∠ABC=90°，证出结论．

【解答】（1）证明：∵△ABC和△DBE是等腰直角三角形，

∴AB=BC，BD=BE，∠ABC=∠DBE=90°，

∴∠ABC﹣∠DBC=∠DBE﹣∠DBC，

即∠ABD=CBE，

在△ABD和△CBE中，

，

∴△ABD≌△CBE（SAS），

∴AD=CE；

（2）延长AD分别交BC和CE于G和F，如图所示：

∵△ABD≌△CBE，

∴∠BAD=∠BCE，

∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°，

又∵∠BGA=∠CGF，

∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°，

∴∠AFC=∠ABC=90°，

∴AD⊥CE．

第150题

甲、乙两同学玩“托球赛跑”游戏，商定：用球拍托着乒乓球从起跑线l起跑，绕过P点跑回到起跑线（如图所示）；途中乒乓球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲同学由于心急，掉了球，浪费了6秒钟，乙同学则顺利跑完．事后，甲同学说：“我俩所用的全部时间的和为50秒”，乙同学说：“捡球过程不算在内时，甲的速度是我的1.2倍”．根据图文信息，请问哪位同学获胜？

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】应算出甲乙两人所用时间．等量关系为：（甲同学跑所用时间+6）+乙同学所用时间=50．

【解答】解：设乙同学的速度为x米/秒，则甲同学的速度为1.2x米/秒，

根据题意，得，

解得x=2.5．

经检验，x=2.5是方程的解，且符合题意．

∴甲同学所用的时间为：（秒），

乙同学所用的时间为：（秒）．

∵26＞24，

∴乙同学获胜．

答：乙同学获胜．

第151题

如果三角形的三个内角的度数比是2：3：4，则它是（　　）

A.锐角三角形

B.钝角三角形

C.直角三角形

D.钝角或直角三角形

参考答案：A

解析：

【考点】三角形内角和定理．

【分析】利用“设k法”求出最大角的度数，然后作出判断即可．

【解答】解：设三个内角分别为2k、3k、4k，

则2k+3k+4k=180°，

解得k=20°，

所以，最大的角为4×20°=80°，

所以，三角形是锐角三角形．

故选A．

第152题

在，，，，中，分式的个数为（　　）

A.2

B.3

C.4

D.5

参考答案：A

解析：

【考点】分式的定义．

【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．

【解答】解：，，的分母中均不含有字母，因此它们是整式，而不是分式．

，的分母中含有字母，因此是分式．

故选：A．

第153题

下列代数运算正确的是（　　）

A.（x³）²=x⁵

B.（2x）²=2x²

C.（x+1）³•x²=x⁵

D.x³•x²=x⁵

参考答案：D

解析：

【考点】幂的乘方与积的乘方；同底数幂的乘法．

【分析】直接利用幂的乘方运算法则以及结合积的乘方运算法则、同底数幂的乘法运算法则分别化简求出答案．

【解答】解：A、（x³）²=x⁶，故此选项错误；

B、（2x）²=4x²，故此选项错误；

C、（x+1）³•x²，不能直接计算，故此选项错误；

D、x³•x²=x⁵，正确．

故选：D．

第154题

下列因式分解正确的是（　　）

A.2x²﹣2=2（x+1）（x﹣1）

B.x²+2x﹣1=（x﹣1）²

C.x²+1=（x+1）²

D.x²﹣x+2=x（x﹣1）+2

参考答案：A

解析：

【考点】提公因式法与公式法的综合运用．

【分析】A直接提出公因式a，再利用平方差公式进行分解即可；B和C不能运用完全平方公式进行分解；D是和的形式，不属于因式分解．

【解答】解：A、2x²﹣2=2（x²﹣1）=2（x+1）（x﹣1），故此选项正确；

B、x²﹣2x+1=（x﹣1）²，故此选项错误；

C、x²+1，不能运用完全平方公式进行分解，故此选项错误；

D、x²﹣x+2=x（x﹣1）+2，还是和的形式，不属于因式分解，故此选项错误；

故选：A．

第155题

已知点A（a，2013）与点B关于x轴对称，则a+b的值为（　　）

A.﹣1

B.1

C.2

D.3

参考答案：B

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】根据关于x轴对称点的坐标的特点，可以得到点A的坐标与点B的坐标的关系．

【解答】解：∵A（a，2013）与点B关于x轴对称，

∴a=2014，b=﹣2013

∴a+b=1，

故选：B．

第156题

根据已知条件，能画出唯一△ABC的是（　　）

A.AC=4，AB=5，BC=10

B.AC=4，AB=5，∠B=60°

C.∠A=50°，∠B=60°，AB=2

D.∠C=90°，AB=5

参考答案：C

解析：

【考点】全等三角形的判定．

【分析】根据若想画出唯一的△ABC只需能找出给定条件能证出与另一三角形全等即可，结合全等三角形的判定定理逐项分析四个选项即可得出结论．

【解答】解：若想画出唯一的△ABC只需能找出给定条件能证出与另一三角形全等即可．

A、AC+AB=4+5=9＜10=BC，三边不等组成三角形，A不正确；

B、∵AC=4，AB=5，∠B=60°，SSA不能证出两三角形全等，

∴AC=4，AB=5，∠B=60°不能确定唯一的三角形，B不正确；

C、∵∠A=50°，∠B=60°，AB=2，ASA能证出两三角形全等，

∴∠A=50°，∠B=60°，AB=2能确定唯一的三角形，C正确；

D、∵∠C=90°，AB=5，确实证明两三角形全等的条件，

∴∠C=90°，AB=5不能确实唯一的三角形，D不正确．

故选C．

第157题

在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°﹣∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：D

解析：

【考点】三角形内角和定理．

【分析】根据三角形的内角和定理得出∠A+∠B+∠C=180°，再根据已知的条件逐个求出∠C的度数，即可得出答案．

【解答】解：①∵∠A+∠B=∠C，∠A+∠B+∠C=180°，

∴2∠C=180°，

∴∠C=90°，

∴△ABC是直角三角形，∴①正确；

②∵∠A：∠B：∠C=1：2：3，∠A+∠B+∠C=180°，

∴∠C=×180°=90°，

∴△ABC是直角三角形，∴②正确；

③∵∠A=90°﹣∠B，

∴∠A+∠B=90°，

∵∠A+∠B+∠C=180°，

∴∠C=90°，

∴△ABC是直角三角形，∴③正确；

④∵∠A=∠B=∠C，

∴∠C=2∠A=2∠B，

∵∠A+∠B+∠C=180°，

∴∠A+∠A+2∠A=180°，

∴∠A=45°，

∴∠C=90°，

∴△ABC是直角三角形，∴④正确；

故选D．

第158题

如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）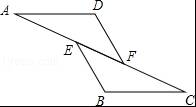

A.∠A=∠C

B.AD=CB

C.BE=DF

D.AD//BC

参考答案：B

解析：

【考点】全等三角形的判定．

【分析】求出AF=CE，再根据全等三角形的判定定理判断即可．

【解答】解：∵AE=CF，

∴AE+EF=CF+EF，

∴AF=CE，

A、∵在△ADF和△CBE中

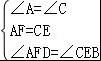
∴△ADF≌△CBE（ASA），正确，故本选项错误；

B、根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；

C、∵在△ADF和△CBE中

∴△ADF≌△CBE（SAS），正确，故本选项错误；

D、∵AD∥BC，

∴∠A=∠C，

∵在△ADF和△CBE中

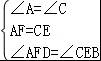
∴△ADF≌△CBE（ASA），正确，故本选项错误；

故选B．

第159题

如果把分式中的x，y都扩大3倍，那么分式的值（　　）

A.扩大3倍

B.不变

C.缩小3倍

D.扩大2倍

参考答案：B

解析：

【考点】分式的基本性质．

【分析】依题意，分别用3x和3y去代换原分式中的x和y，利用分式的基本性质化简即可．

【解答】解：分别用3x和3y去代换原分式中的x和y，

得==，

可见新分式与原分式相等．

故选B．

第160题

下列各分式中，最简分式是（　　）

A.

B.

C.

D.

参考答案：C

解析：

【考点】最简分式．

【分析】最简分式是指分子和分母没有公因式．

【解答】解：（A）原式=，故A不是最简分式；

（B）原式==，故B不是最简分式；

（C）原式=，故C是最简分式；

（D）原式==，故D不是最简分式；

故选（C）