八年级（上）期末数学试卷集（305题）

---

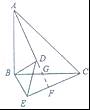
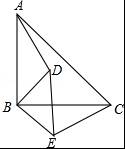
已知：如图，△ABC和△DBE均为等腰直角三角形．

（1）求证：AD=CE；

（2）求证：AD和CE垂直．

知识点：试卷06

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等腰直角三角形．

【分析】（1）由等腰直角三角形的性质得出AB=BC，BD=BE，∠ABC=∠DBE=90°，得出∠ABD=CBE，证出△ABD≌△CBE（SAS），得出AD=CE；

（2）△ABD≌△CBE得出∠BAD=∠BCE，再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°，得出∠AFC=∠ABC=90°，证出结论．

【解答】（1）证明：∵△ABC和△DBE是等腰直角三角形，

∴AB=BC，BD=BE，∠ABC=∠DBE=90°，

∴∠ABC﹣∠DBC=∠DBE﹣∠DBC，

即∠ABD=CBE，

在△ABD和△CBE中，

，

∴△ABD≌△CBE（SAS），

∴AD=CE；

（2）延长AD分别交BC和CE于G和F，如图所示：

∵△ABD≌△CBE，

∴∠BAD=∠BCE，

∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°，

又∵∠BGA=∠CGF，

∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°，

∴∠AFC=∠ABC=90°，

∴AD⊥CE．