第81题

若点P（1，a）与Q（b，2）关于x轴对称，则代数式（a+b）²⁰¹⁵的值为（　　）

A.﹣1

B.1

C.﹣2

D.2

参考答案：A

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．

【解答】解：∵点P（1，a）与Q（b，2）关于x轴对称，

∴a=﹣2，b=1，

∴（a+b）²⁰¹⁵=﹣1．

故选A．

第82题

图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（　　）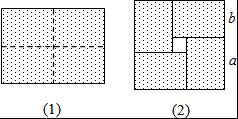

A.ab

B.（a+b）²

C.（a﹣b）²

D.a²﹣b²

参考答案：C

解析：

【考点】完全平方公式的几何背景．

【分析】中间部分的四边形是正方形，表示出边长，则面积可以求得．

【解答】解：中间部分的四边形是正方形，边长是a+b﹣2b=a﹣b，

则面积是（a﹣b）²．

故选：C．

第83题

小强是一位密码翻译爱好者，在他的密码手册中，有这样一条信息：a﹣b，x﹣y，x+y，a+b，x²﹣y²，a²﹣b²分别对应下列六个字：北、爱、我、河、游、美，现将（x²﹣y²）a²﹣（x²﹣y²）b²因式分解，结果呈现的密码信息可能是（　　）

A.我爱美

B.河北游

C.爱我河北

D.美我河北

参考答案：C

解析：

【考点】因式分解的应用．

【分析】将原式进行因式分解即可求出答案

【解答】解：原式=（x²﹣y²）（a²﹣b²）=（x﹣y）（x+y）（a﹣b）（a+b）

由题意可知：（x﹣y）（x+y）（a﹣b）（a+b）可表示为“爱我河北”

故选（C）

第84题

在求3x的倒数的值时，嘉淇同学误将3x看成了8x，她求得的值比正确答案小5．依上述情形，所列关系式成立的是（　　）

A. =﹣5

B. =+5

C. =8x﹣5

D. =8x+5

参考答案：B

解析：

【考点】由实际问题抽象出分式方程．

【分析】根据题意知：8x的倒数+5=3x的倒数，据此列出方程即可．

【解答】解：根据题意，可列方程： =+5，

故选：B．

第85题

工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C作射线OC．由此作法便可得△MOC≌△NOC，其依据是（　　）

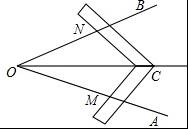
A.SSS

B.SAS

C.ASA

D.AAS

参考答案：A

解析：

【考点】全等三角形的判定．

【分析】由作图过程可得MO=NO，NC=MC，再加上公共边CO=CO可利用SSS定理判定△MOC≌△NOC．

【解答】解：∵在△ONC和△OMC中，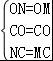

∴△MOC≌△NOC（SSS），

∴∠BOC=∠AOC，

故选：A．

第86题

若a+b=﹣3，ab=1，则a²+b²=（　　）

A.﹣11

B.11

C.﹣7

D.7

参考答案：D

解析：

【考点】完全平方公式．

【分析】根据a²+b²=（a+b）²﹣2ab，直接代入求值即可．

【解答】解：当a+b=﹣3，ab=1时，

a²+b²=（a+b）²﹣2ab=9﹣2=7．

故选D．

第87题

如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S_△ABD=15，则CD的长为（　　）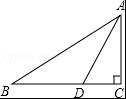

A.3

B.4

C.5

D.6

参考答案：A

解析：

【考点】角平分线的性质．

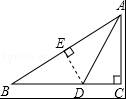
【分析】过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，然后利用△ABD的面积列式计算即可得解．

【解答】解：如图，过点D作DE⊥AB于E，

∵∠C=90°，AD平分∠BAC，

∴DE=CD，

∴S_△ABD=AB•DE=×10•DE=15，

解得DE=3．

故选A．

第88题

如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则△ADE的形状是（　　）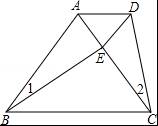

A.等腰三角形

B.等边三角形

C.不等边三角形

D.不能确定形状

参考答案：B

解析：

【考点】等边三角形的判定．

【分析】先证得△ABE≌△ACD，可得AE=AD，∠BAE=∠CAD=60°，即可证明△ADE是等边三角形．

【解答】解：∵△ABC为等边三角形

∴AB=AC

∵∠1=∠2，BE=CD

∴△ABE≌△ACD

∴AE=AD，∠BAE=∠CAD=60°

∴△ADE是等边三角形．

故选B．

第89题

若m=2¹⁰⁰，n=3⁷⁵，则m、n的大小关系正确的是（　　）

A.m＞n

B.m＜n

C.相等

D.大小关系无法确定

参考答案：B

解析：

【考点】幂的乘方与积的乘方．

【分析】根据幂的乘方法则，将每一个数化为指数相同的数，再比较底数．

【解答】解：∵m=2¹⁰⁰=（2⁴）²⁵=16²⁵，n=3⁷⁵=（3³）²⁵=27²⁵，

∴2¹⁰⁰＜3⁷⁵，即m＜n．

故选B．

第90题

如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF；（4）EF垂直平分AD．其中正确的有（　　）

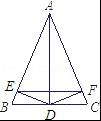
A.1个

B.2个

C.3个

D.4个

参考答案：C

解析：

【考点】等腰三角形的判定与性质；线段垂直平分线的性质．

【分析】利用等腰三角形的概念、性质以及角平分线的性质做题．

【解答】解：∵AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC

∴△ABC是等腰三角形，AD⊥BC，BD=CD，∠BED=∠DFC=90°

∴DE=DF

∴AD垂直平分EF

∴（4）错误；

又∵AD所在直线是△ABC的对称轴，

∴（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF．

故选C．

第91题

分解因式：3a³﹣12a²+12a=　　．

参考答案：

3a（a﹣2）²

解析：

【考点】提公因式法与公式法的综合运用．

【分析】首先提取公因式3a，再利用完全平方公式进行二次分解即可．

【解答】解：原式=3a（a²﹣4a+4）=3a（a﹣2）²，

故答案为：3a（a﹣2）²．

第92题

若一个三角形三个内角的度数之比为1：2：3，则这个三角形中的最大的角度是　　．

参考答案：90°

解析：

【考点】三角形内角和定理．

【分析】已知三角形三个内角的度数之比，可以设一份为k，根据三角形的内角和等于180°列方程求三个内角的度数，从而确定三角形的最大角的度数．

【解答】解：设三个内角的度数分别为k，2k，3k．

则k+2k+3k=180°，

解得k=30°，

则2k=60°，3k=90°，

这个三角形最大的角等于90°．

故答案为：90°．

第93题

我们知道；；；…根据上述规律，计算=　　．

参考答案：9/10

解析：

【考点】规律型：数字的变化类．

【分析】分别根据题意把对应的分式拆分成差的形式，则原式=（1﹣）+（﹣）+（﹣）+…（﹣）=1﹣=．

【解答】解：原式=（1﹣）+（﹣）+（﹣）+…（﹣）=1﹣=．

第94题

如图，在等边△ABC中，AD⊥BC于D，若AB=4cm，AD=2cm，E为AB的中点，P为AD上一点，PE+PB的最小值为　　．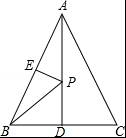

参考答案：2√3

解析：

【考点】轴对称-最短路线问题；等边三角形的性质．

【分析】连接EC交于AD于点P，由等腰三角形三线和一的性质可知AD是BC的垂直平分线，从而可证明BP=PC，故此PE+PB的最小值=EC，然后证明△ACE≌△CAD，从而得到EC=AD．

【解答】解：连接EC交于AD于点P．

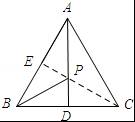
∵AB=AC，BD=DC，

∴AD⊥BC．

∴AD是BC的垂直平分线．

∴PB=PC．

∴PE+PB=EP+PC=EC．

∵△ABC为等边三角形，

∴∠EAC=∠ACD=60°，AB=BC．

∵点E和点D分别是AB和BC的中点，

∴AE=DC．

在△ACE和△CAD中，，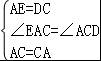

∴△ACE≌△CAD．

∴EC=AD=2．

故答案为：2．

第95题

先简化，再求值：（1+）÷，其中x=3．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，将x的值代入计算即可求出值．

【解答】解：原式=•

=•

=，

当x=3时，原式==．

第96题

解方程：．

参考答案：见解析

解析：

【考点】解分式方程．

【分析】观察可得2﹣x=﹣（x﹣2），所以可确定方程最简公分母为：（x﹣2），然后去分母将分式方程化成整式方程求解．注意检验．

【解答】解：方程两边同乘以（x﹣2），

得：x﹣3+（x﹣2）=﹣3，

解得x=1，

检验：x=1时，x﹣2≠0，

∴x=1是原分式方程的解．

第97题

如图1为L形的一种三格骨牌，它是由三个全等的正方形连接而成．

请以L形的三格骨牌为基本图形，在图2和图3中各设计1个轴对称图形．要求如下：

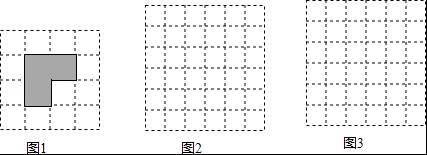
参考答案：见解析

解析：

【考点】利用轴对称设计图案．

【分析】可以利用轴对称设计一个图案，再利用平移设计一个图案即可．

【解答】解：如图所示：

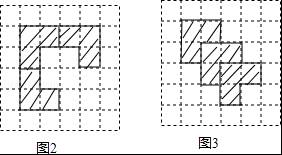
第98题

如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB，求∠A的度数．

参考答案：见解析

解析：

【考点】三角形的外角性质；三角形内角和定理．

【分析】根据同一个三角形中等边对等角的性质，设∠ABD=x，结合三角形外角的性质，则可用x的代数式表示∠A、∠ABC、∠C，再在△ABC中，运用三角形的内角和为180°，可求∠A的度数．

【解答】解：∵DE=EB

∴设∠BDE=∠ABD=x，

∴∠AED=∠BDE+∠ABD=2x，

∵AD=DE，

∴∠AED=∠A=2x，

∴∠BDC=∠A+∠ABD=3x，

∵BD=BC，

∴∠C=∠BDC=3x，

∵AB=AC，

∴∠ABC=∠C=3x，

在△ABC中，3x+3x+2x=180°，

解得x=22.5°，

∴∠A=2x=22.5°×2=45°．

第99题

某一工程，在工程招标时，接到甲，乙两个工程队的投标书．施工一天，需付甲工程队工程款1.2万元，乙工程队工程款0.5万元．工程领导小组根据甲，乙两队的投标书测算，有如下方案：

（1）甲队单独完成这项工程刚好如期完成；

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】关键描述语为：“甲，乙两队合做3天，余下的工程由乙队单独做也正好如期完成”；说明甲队实际工作了3天，乙队工作了x天完成任务，工作量=工作时间×工作效率等量关系为：甲3天的工作量+乙规定日期的工作量=1列方程．

再看费用情况：方案（1）、（3）不耽误工期，符合要求，可以求费用，方案（2）显然不符合要求．

【解答】解：设规定日期为x天．由题意得

++=1，

．

3（x+6）+x²=x（x+6），

3x=18，

解之得：x=6．

经检验：x=6是原方程的根．

方案（1）：1.2×6=7.2（万元）；

方案（2）比规定日期多用6天，显然不符合要求；

方案（3）：1.2×3+0.5×6=6.6（万元）．

∵7.2＞6.6，

∴在不耽误工期的前提下，选第三种施工方案最节省工程款．

第100题

情景观察：

如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

参考答案：见解析

解析：

【考点】三角形综合题．

【分析】情境观察：①由全等三角形的判定方法容易得出结果；

②由全等三角形的性质即可得出结论；

问题探究：延长AB、CD交于点G，由ASA证明△ADC≌△ADG，得出对应边相等CD=GD，即CG=2CD，证出∠BAE=∠BCG，由ASA证明△ADC≌△CBG，得出AE=CG=2CD即可．

拓展延伸：作DG⊥BC交CE的延长线于G，同上证明三角形全等，得出DF=CG即可．

【解答】解：情境观察：

①∵AE⊥BC，

∴∠AEC=∠AEB=90°，

在Rt△AEB和Rt△AEC中，

∵，

∴△ABE≌△ACE（HL），

∵CD⊥AB，∠BAC=45°，

∴AD=CD，

∵AB=AC，∠BAC=45°，

∴=67.5°，

∴∠BCD=90°﹣∠B=22.5°，

又∵∠FAD=∠BAC=22.5°，

∴∠BCD=∠FAD，

在△BCD和△FAD中，

∵，

∴△BCD≌△FAD（ASA），

故答案为：△ABE≌△ACE，△ADF≌△CDB；

②线段AF与线段CE的数量关系是：AF=2CE；

∵△BCD≌△FAD，

∴AF=BC，

又∵AB=AC，且AE⊥BC，

∴BC=2CE，

∴AF=2CE，

故答案为：AF=2CE．

问题探究：

延长AB、CD交于点G，如图2所示：

∵AD平分∠BAC，

∴∠CAD=∠GAD，

∵AD⊥CD，

∴∠ADC=∠ADG=90°，

在△ADC和△ADG中，

∵，

∴△ADC≌△ADG（ASA），

∴CD=GD，即CG=2CD，

∵∠BAC=45°，AB=BC，

∴∠ABC=90°，

∴∠CBG=90°，

∴∠G+∠BCG=90°，

∵∠G+∠BAE=90°，

∴∠BAE=∠BCG，

在△ABE和△CBG中，

∵，

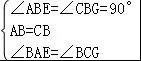∴△ADC≌△CBG中（ASA），

∴AE=CG=2CD．

拓展延伸：如图3所示．作DG⊥BC于点H，交CE的延长线于G，

∵∠BAC=45°，AB=BC，

∴AB⊥BC，

∴DG∥AB，

∴∠GDC=∠BAC=45°，

∴∠EDC=∠BAC=22.5°=∠EDG，DH=CH，

又∵DE⊥CE，

∴∠DEC=∠DEG=90°，

在△DEC和△DEG中，

∵，

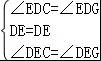∴△DEC≌△DEG（ASA），

∴DC=DG，

∵∠DHF=∠CEF=90°，∠DFH=∠CFE，

∴∠FDH=∠GCH，

在△DHF和△CHG中，

∵，

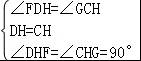∴△DHF≌△CHG（ASA），

∴DF=CG=2CE．