第21题

从广州到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的1.3倍．

（1）求普通列车的行驶路程；

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】（1）根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍，两数相乘即可得出答案；

（2）设普通列车平均速度是x千米/时，根据高铁所需时间比乘坐普通列车所需时间缩短3小时，列出分式方程，然后求解即可；

【解答】解：（1）根据题意得：

400×1.3=520（千米），

答：普通列车的行驶路程是520千米；

（2）设普通列车平均速度是x千米/时，则高铁平均速度是2.5x千米/时，根据题意得：

﹣=3，

解得：x=120，

经检验x=120是原方程的解，

则高铁的平均速度是120×2.5=300（千米/时），

答：高铁的平均速度是300千米/时．

第22题

如图，点D在△ABC的AB边上，且∠ACD=∠A．

（1）作∠BDC的平分线DE，交BC于点E（用尺规作图法，保留作图痕迹，不要求写作法）；

参考答案：见解析

解析：

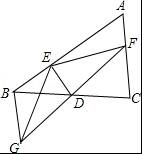
【考点】作图—基本作图；平行线的判定．

【分析】（1）根据角平分线基本作图的作法作图即可；

（2）根据角平分线的性质可得∠BDE=∠BDC，根据三角形内角与外角的性质可得∠A=∠BDC，再根据同位角相等两直线平行可得结论．

【解答】解：（1）如图所示：

（2）DE∥AC

∵DE平分∠BDC，

∴∠BDE=∠BDC，

∵∠ACD=∠A，∠ACD+∠A=∠BDC，

∴∠A=∠BDC，

∴∠A=∠BDE，

∴DE∥AC．

第23题

如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．

（1）求证：BG=CF；

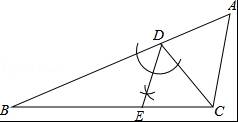
参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【分析】（1）先利用ASA判定△BGD≌△CFD，从而得出BG=CF；

（2）再利用全等的性质可得GD=FD，再有DE⊥GF，从而得出EG=EF，两边和大于第三边从而得出BE+CF＞EF．

【解答】解：（1）∵BG∥AC，

∴∠DBG=∠DCF．

∵D为BC的中点，

∴BD=CD

又∵∠BDG=∠CDF，

在△BGD与△CFD中，

∵

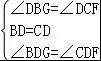
∴△BGD≌△CFD（ASA）．

∴BG=CF．

（2）BE+CF＞EF．

∵△BGD≌△CFD，

∴GD=FD，BG=CF．

又∵DE⊥FG，

∴EG=EF（垂直平分线到线段端点的距离相等）．

∴在△EBG中，BE+BG＞EG，

即BE+CF＞EF．

第24题

若分式有意义，则x应满足的条件是（　　）

A.x≠0

B.x≥3

C.x≠3

D.x≤3

参考答案：C

解析：

【考点】分式有意义的条件．

【专题】压轴题．

【分析】本题主要考查分式有意义的条件：分母≠0．

【解答】解：∵x﹣3≠0，

∴x≠3．

故选C．

【点评】本题考查的是分式有意义的条件．当分母不为0时，分式有意义．

第25题

若下列各组值代表线段的长度，能组成三角形的是（　　）

A.1、2、3.5

B.4、5、9

C.5、15、8

D.20、15、8

参考答案：D

解析：

【考点】三角形三边关系．

【专题】探究型．

【分析】根据三角形两边之和大于第三边和两边之差小于第三边可以判断选项中的数据是否能组成三角形，本题得以解决．

【解答】解：∵1+2＜3.5，∴选项A中的数据不能组成三角形；

∵4+5=9，∴选项B中的数据不能组成三角形；

∵5+8＜15∴选项C中的数据不能组成三角形；

∵15+8＞20∴选项D中的数据能组成三角形；

故选D．

【点评】本题考查三角形三边的关系，解题的关键是明确三角形两边之和大于第三边和两边之差小于第三边．

第26题

如图，AB=AD，BC=CD，那么全等三角形的对数是（　　）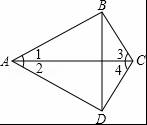

A.1

B.2

C.3

D.4

参考答案：C

解析：

【考点】全等三角形的判定．

【分析】先根据SSS推出△ABC≌△ADC，推出∠1=∠2，∠3=∠4，再根据SAS即可推出△ABO≌△ADO，△CBO≌△CDO．

【解答】解：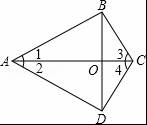

全等三角形有△ABC≌△ADC，△ABO≌△ADO，△CBO≌△CDO，共3对，

故选C．

【点评】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理是：SAS，ASA，AAS，SSS．

第27题

如图，在△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD等于（　　）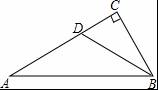

A.3

B.4

C.5

D.6

参考答案：A

解析：

【考点】含30度角的直角三角形．

【分析】由于∠C=90°，∠ABC=60°，可以得到∠A=30°，又由BD平分∠ABC，可以推出∠CBD=∠ABD=∠A=30°，BD=AD=6，再30°角所对的直角边等于斜边的一半即可求出结果．

【解答】解：∵∠C=90°，∠ABC=60°，

∴∠A=30°，

∵BD平分∠ABC，

∴∠CBD=∠ABD=∠A=30°，

∴BD=AD=6，

∴CD=BD=6×=3．

故选A．

【点评】本题主要考查了等腰三角形的性质和判定，三角形的内角和定理，含30度角的直角三角形性质的应用，关键是求出BD的长和得出CD=BD．

第28题

下列运算中正确的是（　　）

A.（x³）²=x⁵

B.2a^﹣5•a³=2a⁸

C.6x³÷（﹣3x²）=2x

D.3^﹣2=

参考答案：D

解析：

【考点】整式的除法；幂的乘方与积的乘方；负整数指数幂．

【分析】根据幂的乘方、单项式的乘方、除法法则以及负指数次幂的意义即可判断．

【解答】解：A、（x³）²=x⁶，选项错误；

B、2a^﹣5•a³=2a^﹣2=，选项错误；

C、6x³÷（﹣3x²）=﹣2x，选项错误；

D、3^﹣2==，选项正确．

故选D．

【点评】本题考查了单项式除单项式，用整式乘除解决实际问题时要注意分清量与量之间存在的数量关系．

第29题

如图，已知∠1=∠2，要得到△ABD≌△ACD，还需从下列条件中补选一个，则错误的选法是（　　）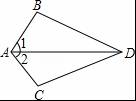

A.AB=AC

B.DB=DC

C.∠ADB=∠ADC

D.∠B=∠C

参考答案：B

解析：

【考点】全等三角形的判定．

【分析】先要确定现有已知在图形上的位置，结合全等三角形的判定方法对选项逐一验证，排除错误的选项．本题中C、AB=AC与∠1=∠2、AD=AD组成了SSA是不能由此判定三角形全等的．

【解答】解：A、∵AB=AC，

∴，

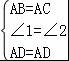∴△ABD≌△ACD（SAS）；故此选项正确；

B、当DB=DC时，AD=AD，∠1=∠2，

此时两边对应相等，但不是夹角对应相等，故此选项错误；

C、∵∠ADB=∠ADC，

∴，

∴△ABD≌△ACD（ASA）；故此选项正确；

D、∵∠B=∠C，

∴，

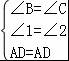∴△ABD≌△ACD（AAS）；故此选项正确．

故选：B．

【点评】本题考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，但SSA无法证明三角形全等．

第30题

下列图形中，不一定是轴对称图形的是（　　）

A.直角三角形

B.线段

C.钝角

D.等腰三角形

参考答案：A

解析：

【考点】轴对称图形．

【分析】根据轴对称图形的概念容易得出结果．

【解答】解：B、C、D都是轴对称图形；

A、不一定是轴对称图形，若三角形不是等腰直角三角形就不是轴对称图形．

故选：A．

【点评】本题考查了轴对称图形的知识，注意掌握轴对称图形的判断方法：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．

第31题

如果=3，则=（　　）

A.

B.xy

C.4

D.

参考答案：C

解析：

【考点】分式的基本性质．

【专题】计算题．

【分析】由=3，得x=3y，再代入所求的式子化简即可．

【解答】解：由=3，得x=3y，

把x=3y代入==4，

故选C．

【点评】找出x、y的关系，代入所求式进行约分．

第32题

货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x千米/小时，依题意列方程正确的是（　　）

A.

B.

C.

D.

参考答案：C

解析：

【考点】由实际问题抽象出分式方程．

【分析】题中等量关系：货车行驶25千米与小车行驶35千米所用时间相同，列出关系式．

【解答】解：根据题意，得

．

故选：C．

【点评】理解题意是解答应用题的关键，找出题中的等量关系，列出关系式．

第33题

如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（　　）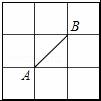

A.6

B.7

C.8

D.9

参考答案：C

解析：

【考点】等腰三角形的判定．

【专题】分类讨论．

【分析】根据题意，结合图形，分两种情况讨论：①AB为等腰△ABC底边；②AB为等腰△ABC其中的一条腰．

【解答】解：如上图：分情况讨论．

①AB为等腰△ABC底边时，符合条件的C点有4个；

②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．

故选：C．

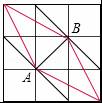
【点评】本题考查了等腰三角形的判定；解答本题关键是根据题意，画出符合实际条件的图形，再利用数学知识来求解．数形结合的思想是数学解题中很重要的解题思想．

第34题

若分式的值为0，则x的值为　　．

参考答案：3

解析：

【考点】分式的值为零的条件．

【专题】计算题．

【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0．两个条件需同时具备，缺一不可．据此可以解答本题．

【解答】解：由题意可得x﹣3=0且x+3≠0，

解得x=3．

故答案为：3．

【点评】本题主要考查了分式的值为0的条件．由于该类型的题易忽略分母不为0这个条件，所以常以这个知识点来命题．

第35题

三角形三边的长分别为8、19、a，则边a的取值范围是　　．

参考答案：11＜a＜27

解析：

【考点】三角形三边关系．

【专题】推理填空题．

【分析】根据三角形中的两边之和大于第三边和两边之差小于第三边进行计算即可解答本题．

【解答】解：∵三角形三边的长分别为8、19、a，

∴19﹣8＜a＜19+8，

∴11＜a＜27，

故答案为：11＜a＜27．

【点评】本题考查三角形的三边关系，解题的关键是明确两边之和大于第三边和两边之差小于第三边．

第36题

已知x²+mx+9是完全平方式，则常数m等于　　．

参考答案：±6

解析：

【考点】完全平方式．

【分析】完全平方式有a²+2ab+b²和a²﹣2ab+b²两个，根据已知得出mx=±2•x•3，求出即可．

【解答】解：x²+mx+9=x²+mx+3²，

∵x²+mx+9是完全平方式，

∴mx=±2•x•3，

解得：m=±6，

故答案为：±6．

【点评】本题考查了对完全平方式的应用，能求出符合的两个值是解此题的关键，注意：完全平方式有a²+2ab+b²和a²﹣2ab+b²两个．

第37题

已知点A（a，1）和B（2，b）关于x轴对称，则（a+b）²⁰¹⁵=　　．

参考答案：1

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得a、b的值，根据1的任何次幂都是1，可得答案．

【解答】解：由点A（a，1）和B（2，b）关于x轴对称，得

a=2，b=﹣1．

（a+b）²⁰¹⁵=1，

故答案为：1．

【点评】本题考查了关于x轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．

第38题

已知：a+b=，ab=1，化简（a﹣2）（b﹣2）的结果是　　．

参考答案：2

解析：

【考点】整式的混合运算—化简求值．

【专题】整体思想．

【分析】根据多项式相乘的法则展开，然后代入数据计算即可．

【解答】解：（a﹣2）（b﹣2）

=ab﹣2（a+b）+4，

当a+b=，ab=1时，原式=1﹣2×+4=2．

故答案为：2．

【点评】本题考查多项式相乘的法则和整体代入的数学思想．

第39题

分解因式：3a³﹣12a=　　．

参考答案：3a（a+2）（a﹣2）

解析：

【考点】提公因式法与公式法的综合运用．

【分析】先提取公因式3a，再对余下的多项式利用平方差公式继续分解．

【解答】解：3a³﹣12a

=3a（a²﹣4），

=3a（a+2）（a﹣2）．

故答案为：3a（a+2）（a﹣2）．

【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．

第40题

在△ABC中，AB=AC，AB的垂直平分线DE交AC于D，交AB于E，∠ADE=50°，则∠B=　　．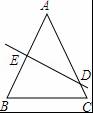

参考答案：70°

解析：

【考点】线段垂直平分线的性质；等腰三角形的性质．

【分析】根据线段垂直平分线的概念得到∠AED=90°，求出∠A=40°，根据三角形内角和定理和等腰三角形的性质计算即可．

【解答】解：∵DE是AB的垂直平分线，

∴DE⊥AB，

∴∠AED=90°，又∠ADE=50°，

∴∠A=40°，又AB=AC，

∴∠B=∠C=70°，

故答案为：70°．

【点评】本题考查的是线段垂直平分线的概念和等腰三角形的性质，掌握三角形内角和等于180°、等腰三角形等边对等角是解题的关键．