八年级（上）期末数学试卷集（305题）

---

情景观察：

如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

①写出图1中所有的全等三角形　　；

②线段AF与线段CE的数量关系是　　．

问题探究：

如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．

求证：AE=2CD．

拓展延伸：

如图3，△ABC中，∠BAC=45°，AB=BC，点D在AC上，∠EDC=∠BAC，DE⊥CE，垂足为E，DE与BC交于点F．求证：DF=2CE．

要求：请你写出辅助线的作法，并在图3中画出辅助线，不需要证明．

知识点：试卷04

参考答案：见解析

解析：

【考点】三角形综合题．

【分析】情境观察：①由全等三角形的判定方法容易得出结果；

②由全等三角形的性质即可得出结论；

问题探究：延长AB、CD交于点G，由ASA证明△ADC≌△ADG，得出对应边相等CD=GD，即CG=2CD，证出∠BAE=∠BCG，由ASA证明△ADC≌△CBG，得出AE=CG=2CD即可．

拓展延伸：作DG⊥BC交CE的延长线于G，同上证明三角形全等，得出DF=CG即可．

【解答】解：情境观察：

①∵AE⊥BC，

∴∠AEC=∠AEB=90°，

在Rt△AEB和Rt△AEC中，

∵，

∴△ABE≌△ACE（HL），

∵CD⊥AB，∠BAC=45°，

∴AD=CD，

∵AB=AC，∠BAC=45°，

∴=67.5°，

∴∠BCD=90°﹣∠B=22.5°，

又∵∠FAD=∠BAC=22.5°，

∴∠BCD=∠FAD，

在△BCD和△FAD中，

∵，

∴△BCD≌△FAD（ASA），

故答案为：△ABE≌△ACE，△ADF≌△CDB；

②线段AF与线段CE的数量关系是：AF=2CE；

∵△BCD≌△FAD，

∴AF=BC，

又∵AB=AC，且AE⊥BC，

∴BC=2CE，

∴AF=2CE，

故答案为：AF=2CE．

 

问题探究：

延长AB、CD交于点G，如图2所示：

∵AD平分∠BAC，

∴∠CAD=∠GAD，

∵AD⊥CD，

∴∠ADC=∠ADG=90°，

在△ADC和△ADG中，

∵，

∴△ADC≌△ADG（ASA），

∴CD=GD，即CG=2CD，

∵∠BAC=45°，AB=BC，

∴∠ABC=90°，

∴∠CBG=90°，

∴∠G+∠BCG=90°，

∵∠G+∠BAE=90°，

∴∠BAE=∠BCG，

在△ABE和△CBG中，

∵，

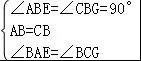∴△ADC≌△CBG中（ASA），

∴AE=CG=2CD．

 

拓展延伸：如图3所示．作DG⊥BC于点H，交CE的延长线于G，

∵∠BAC=45°，AB=BC，

∴AB⊥BC，

∴DG∥AB，

∴∠GDC=∠BAC=45°，

∴∠EDC=∠BAC=22.5°=∠EDG，DH=CH，

又∵DE⊥CE，

∴∠DEC=∠DEG=90°，

在△DEC和△DEG中，

∵，

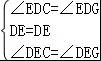∴△DEC≌△DEG（ASA），

∴DC=DG，

∵∠DHF=∠CEF=90°，∠DFH=∠CFE，

∴∠FDH=∠GCH，

在△DHF和△CHG中，

∵，

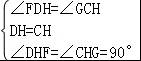∴△DHF≌△CHG（ASA），

∴DF=CG=2CE．