第201题

随着城际铁路的正式开通，从甲市经丙市到乙市的高铁里程比普快里程缩短了90km，运行时间减少了8h，已知甲市到乙市的普快列车里程为1220km．高铁平均时速是普快平均时速的2.5倍．

（1）求高铁列车的平均时速；

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】（1）设普快的平均时速为x千米/小时，高铁列车的平均时速为2.5x千米/小时，根据题意可得，高铁走（1220﹣90）千米比普快走1220千米时间减少了8小时，据此列方程求解；

（2）求出王先生所用的时间，然后进行判断．

【解答】解：（1）设普快的平均时速为x千米/小时，高铁列车的平均时速为2.5x千米/小时，

由题意得，﹣=8，

解得：x=96，

经检验，x=96是原分式方程的解，且符合题意，

则2.5x=240，

答：高铁列车的平均时速为240千米/小时；

（2）780÷240=3.25，

则坐车共需要3.25+1=4.25（小时），

从9：20到下午1：40，共计4小时＞4.25小时，

故王先生能在开会之前到达．

【点评】本题考查了分式方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解，注意检验．

第202题

（1）如图①，等腰直角△ABC中，∠ABC=90°，AB=BC，点A、B分别在坐标轴上，若点C的横坐标为2，直接写出点B的坐标　　；（提示：过C作CD⊥y轴于点D，利用全等三角形求出OB即可）

（2）如图②，若点A的坐标为（﹣6，0），点B在y轴的正半轴上运动时，分别以OB、AB为边在第一、第二象限作等腰直角△OBF，等腰直角△ABE，连接EF交y轴于点P，当点B在y轴的正半轴上移动时，PB的长度是否发生改变？若不变，求出PB的值．若变化，求PB的取值范围．

参考答案：见解析

解析：

【考点】三角形综合题．

【分析】（1）作CD⊥BO，易证△ABO≌△BCD，根据全等三角形对应边相等的性质即可解题；

（2）作EG⊥y轴，易证△BAO≌△EBG和△EGP≌△FBP，可得BG=AO和PB=PG，即可求得PB=AO，即可解题．

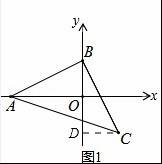
【解答】解：（1）如图1，作CD⊥BO于D，

∵∠CBD+∠ABO=90°，∠ABO+∠BAO=90°，

∴∠CBD=∠BAO，

在△ABO和△BCD中，

，

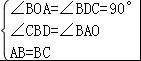∴△ABO≌△BCD（AAS），

∴CD=BO=2，

∴B点坐标（0，2）；

故答案为：（0，2）；

（2）PB的长度不发生改变，

理由：如图3，作EG⊥y轴于G，

∵∠BAO+∠OBA=90°，∠OBA+∠EBG=90°，

∴∠BAO=∠EBG，

在△BAO和△EBG中，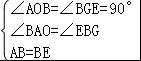

∴△BAO≌△EBG（AAS），

∴BG=AO，EG=OB，

∵OB=BF，

∴BF=EG，

在△EGP和△FBP中，，

∴△EGP≌△FBP（AAS），

∴PB=PG，

∴PB=BG=AO=3

即：PB的长度不发生改变，是定值为3．

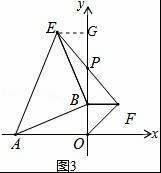
【点评】此题是三角形综合题，主要考查了勾股定理、角平分线的性质、全等三角形的判定与性质，熟练掌握三角形全等的证明是解本题的关键．

第203题

下列计算正确的是（　　）

A.a²•a³=a⁶

B.2a•3a=6a

C.（a²）³=a⁶

D.（a+b）²=a²+b²

参考答案：C

解析：

【考点】整式的混合运算．

【分析】根据同底数幂的乘法、单项式乘以单项式、幂的乘方、完全平方公式分别求出每个式子的值，再判断即可．

【解答】解：A、结果是a⁵，故本选项错误；

B、结果是6a²，故本选项错误；

C、结果是a⁶，故本选项正确；

D、结果是a²+2ab+b²，故本选项错误；

故选C．

第204题

如果三角形的两边长分别为3和5，第三边长是偶数，则第三边长可以是（　　）

A.2

B.3

C.4

D.8

参考答案：C

解析：

【考点】三角形三边关系．

【分析】根据三角形三边关系，可令第三边为X，则5﹣3＜X＜5+3，即2＜X＜8，又因为第三边长为偶数，所以第三边长是4，6．问题可求．

【解答】解：由题意，令第三边为X，则5﹣3＜X＜5+3，即2＜X＜8，

∵第三边长为偶数，∴第三边长是4或6．

∴三角形的第三边长可以为4．

故选C．

第205题

已知点A（m﹣1，3）与点B（2，n+1）关于x轴对称，则m+n的值为（　　）

A.﹣1

B.﹣7

C.1

D.7

参考答案：A

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】本题比较容易，考查平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点：关于y轴对称的点，纵坐标相同，横坐标互为相反数．

【解答】解：∵点A（m﹣1，3）与点B（2，n+1）关于x轴对称，

∴，

∴，

∴m+n=3+（﹣4）=﹣1．

故选A．

第206题

已知图中的两个三角形全等，则∠α的度数是（　　）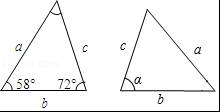

A.72°

B.60°

C.58°

D.50°

参考答案：A

解析：

【考点】全等三角形的性质．

【分析】根据全等三角形对应角相等可知∠α是b、c边的夹角，然后写出即可．

【解答】解：∵两个三角形全等，

∴∠α的度数是72°．

故选A．

第207题

化简的结果是（　　）

A.

B.

C.

D.a+b

参考答案：A

解析：

【考点】分式的加减法．

【分析】异分母的分式相加减，先将分母分解因式，再通分、化简即可．

【解答】解：

=

=．

故选A．

第208题

如图所示，在△ABC中，∠B=47°，∠C=23°，AD是△ABC的角平分线，则∠CAD的度数为（　　）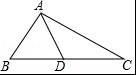

A.40°

B.45°

C.50°

D.55°

参考答案：D

解析：

【考点】三角形内角和定理．

【分析】根据三角形内角和定理求出∠BAC，根据角平分线的定义计算即可．

【解答】解：∵∠B=47°，∠C=23°，

∴∠BAC=180°﹣∠B﹣∠C=110°，

∵AD是△ABC的角平分线，

∴∠CAD=∠BAC=55°，

故选：D．

第209题

在x²﹣y²，﹣x²+y²，（﹣x）²+（﹣y）²，x⁴﹣y²中能用平方差公式分解因式的有（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：C

解析：

【考点】因式分解-运用公式法．

【分析】利用平方差公式的结构特征判断即可．

【解答】解：在x²﹣y²，能；﹣x²+y²，能；（﹣x）²+（﹣y）²，不能；x⁴﹣y²，能，

则能用平方差公式分解因式的有3个，

故选C

第210题

如图，AB=AC，∠BAC=110°，AB的垂直平分线交BC于点D，那么∠ADC=（　　）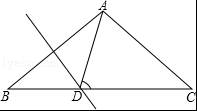

A.50°

B.60°

C.70°

D.80°

参考答案：C

解析：

【考点】等腰三角形的性质；线段垂直平分线的性质．

【分析】先根据等腰三角形内角和定理得出∠B的度数，再由中垂线的知识得出△ABD为等腰直角三角形，可得出∠BAD的度数，根据三角形的一个外角等于与其不相邻的两内角和，即可得出∠ADC的度数．

【解答】解：根据题意，在△ABC中，AB=AC，∠BAC=110°，

∴∠B=35°，

又AB的垂直平分线交BC于点D，

∴∠BAD=∠B=35°，

在△BAD中，∠ADC=∠B+∠BAD=70°，

∴∠ADC=70°．

故答案选C．

第211题

甲乙两人骑自行车从相距S千米的两地同时出发，若同向而行，经过a小时甲追上乙；若相向而行，经过b小时甲、乙相遇．设甲的速度为v₁千米/时，乙的速度为v₂千米/时，则等于（　　）

A.

B.

C.

D.

参考答案：B

解析：

【考点】列代数式（分式）．

【分析】根据题意得到a（v₁﹣v₂）=s，①，b（v₁+v₂）=s，②，由①②，解得v₁，v₂，即可求出答案．

【解答】解：a（v₁﹣v₂）=s，①，b（v₁+v₂）=s，②，

由①②，解得v₁=，v₂=，

=，

故选B

第212题

如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（　　）

A.（2a²+5a）cm²

B.（6a+15）cm²

C.（6a+9）cm²

D.（3a+15）cm²

参考答案：B

解析：

【考点】平方差公式的几何背景．

【分析】大正方形与小正方形的面积的差就是矩形的面积，据此即可求解．

【解答】解：矩形的面积是：（a+4）²﹣（a+1）²

=（a+4+a+1）（a+4﹣a﹣1）

=3（2a+5）

=6a+15（cm²）．

故选B．

第213题

若分式有意义，则x　　．

参考答案：≠1/2

解析：

【考点】分式有意义的条件．

【分析】根据分式有意义的条件可得2x﹣1≠0，再解即可．

【解答】解：由题意得：2x﹣1≠0，

解得：x≠，

故答案为：．

第214题

分式，，的最简公分母是　　．

参考答案：12xy²

解析：

【考点】最简公分母．

【分析】确定最简公分母的方法是：

（1）取各分母系数的最小公倍数；

（2）凡单独出现的字母连同它的指数作为最简公分母的一个因式；

（3）同底数幂取次数最高的，得到的因式的积就是最简公分母．

【解答】解：分式，，的分母分别是2x、3y²、4xy，故最简公分母是12xy²．

故答案为12xy²．

第215题

如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是　　．

参考答案：AO=DO或AB=DC或BO=CO

解析：

【考点】全等三角形的判定．

【分析】本题要判定△AOB≌△DOC，已知∠A=∠D，∠AOB=∠DOC，则可以添加AO=DO或AB=DC或BO=CO从而利用ASA或AAS判定其全等．

【解答】解：添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC．

故填AO=DO或AB=DC或BO=CO．

第216题

已知a，b，c是△ABC的三边，且满足关系式a²+c²=2ab+2bc﹣2b²，则△ABC是　　三角形．

参考答案：等边

解析：

【考点】因式分解的应用．

【分析】先把原式化为完全平方的形式再求解．

【解答】解：∵原式=a²+c²﹣2ab﹣2bc+2b²=0，

a²+b²﹣2ab+c²﹣2bc+b²=0，

即（a﹣b）²+（b﹣c）²=0，

∴a﹣b=0且b﹣c=0，即a=b且b=c，

∴a=b=c．

故△ABC是等边三角形．

故答案为：等边．

第217题

若x²+y²=10，xy=﹣3，则（x+y）²=　　．

参考答案：94

解析：

【考点】完全平方公式．

【分析】根据∴（x+y）²=x²+2xy+y²，代入计算即可．

【解答】解：∵x²+y²=10，xy=﹣3，

∴（x+y）²=x²+2xy+y²=100﹣6=94；

故答案为：94．

第218题

若关于x的方程无解，则m=　　．

参考答案：﹣2

解析：

【考点】分式方程的解．

【分析】分式方程无解的条件是：去分母后所得整式方程无解，或解这个整式方程得到的解使原方程的分母等于0．

【解答】解：去分母得：2=x﹣3﹣m，

解得：x=5+m，

当分母x﹣3=0即x=3时方程无解，

∴5+m=3即m=﹣2时方程无解，则m=﹣2．

故答案为：﹣2．

第219题

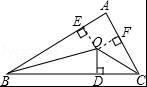
如图，△ABC的周长为22cm，∠ABC，∠ACB的平分线交于O，OD⊥BC于D，且OD=3cm，则△ABC的面积为　　cm²．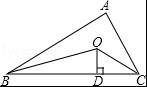

参考答案：33

解析：

【考点】角平分线的性质．

【分析】过点O作OE⊥AB于E，OF⊥AC于F，然后根据角平分线上的点到角的两边的距离相等的性质可得OD=OE=OF，再根据三角形面积计算即可得解．

【解答】解：如图，过点O作OE⊥AB于E，OF⊥AC于F，

∵∠ABC、∠ACB的平分线，OD⊥BC，

∴OD=OE，OD=OF，

∴OD=OE=OF=3cm，

∴△ABC的面积=（AB+BC+AC）×3=33cm²；

故答案为：33．

第220题

如图，P为△ABC内的一点，D、E、F分别是点P关于边AB、BC、CA所在直线的对称点，那么∠ADB+∠BEC+CFA等于　．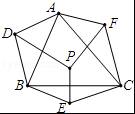

参考答案：360°

解析：

【考点】轴对称的性质．

【分析】连接PA、PB、PC，根据轴对称的性质可得∠DAB=∠PAB，∠FAC=∠PAC，从而求出∠DAF=2∠BAC，同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，再根据六边形的内角和定理列式计算即可得解．

【解答】解：如图，连接PA、PB、PC，

∵D、F分别是点P关于边AB、CA所在直线的对称点，

∴∠DAB=∠PAB，∠FAC=∠PAC，

∴∠DAF=2∠BAC，

同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，

∵∠BAC+∠ABC+∠ACB=180°，

∴∠DAF+∠DBE+∠ECF=180°×2=360°，

∴∠ADB+∠BEC+CFA=（6﹣2）•180°﹣（∠DAF+∠DBE+∠ECF）=720°﹣360°=360°．

故答案为：360°．