八年级（上）期末数学试卷集（305题）

---

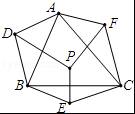
如图，P为△ABC内的一点，D、E、F分别是点P关于边AB、BC、CA所在直线的对称点，那么∠ADB+∠BEC+CFA等于　．

知识点：试卷09

参考答案：360°

解析：

【考点】轴对称的性质．

【分析】连接PA、PB、PC，根据轴对称的性质可得∠DAB=∠PAB，∠FAC=∠PAC，从而求出∠DAF=2∠BAC，同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，再根据六边形的内角和定理列式计算即可得解．

【解答】解：如图，连接PA、PB、PC，

∵D、F分别是点P关于边AB、CA所在直线的对称点，

∴∠DAB=∠PAB，∠FAC=∠PAC，

∴∠DAF=2∠BAC，

同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，

∵∠BAC+∠ABC+∠ACB=180°，

∴∠DAF+∠DBE+∠ECF=180°×2=360°，

∴∠ADB+∠BEC+CFA=（6﹣2）•180°﹣（∠DAF+∠DBE+∠ECF）=720°﹣360°=360°．

故答案为：360°．