八年级（上）期末数学试卷集（305题）

---

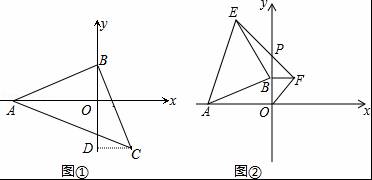
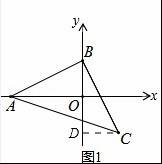
（1）如图①，等腰直角△ABC中，∠ABC=90°，AB=BC，点A、B分别在坐标轴上，若点C的横坐标为2，直接写出点B的坐标　　；（提示：过C作CD⊥y轴于点D，利用全等三角形求出OB即可）

（2）如图②，若点A的坐标为（﹣6，0），点B在y轴的正半轴上运动时，分别以OB、AB为边在第一、第二象限作等腰直角△OBF，等腰直角△ABE，连接EF交y轴于点P，当点B在y轴的正半轴上移动时，PB的长度是否发生改变？若不变，求出PB的值．若变化，求PB的取值范围．

知识点：试卷08

参考答案：见解析

解析：

【考点】三角形综合题．

【分析】（1）作CD⊥BO，易证△ABO≌△BCD，根据全等三角形对应边相等的性质即可解题；

（2）作EG⊥y轴，易证△BAO≌△EBG和△EGP≌△FBP，可得BG=AO和PB=PG，即可求得PB=AO，即可解题．

【解答】解：（1）如图1，作CD⊥BO于D，

∵∠CBD+∠ABO=90°，∠ABO+∠BAO=90°，

∴∠CBD=∠BAO，

在△ABO和△BCD中，

，

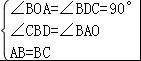∴△ABO≌△BCD（AAS），

∴CD=BO=2，

∴B点坐标（0，2）；

故答案为：（0，2）；

 

（2）PB的长度不发生改变，

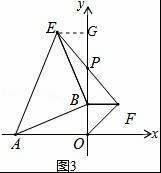
理由：如图3，作EG⊥y轴于G，

∵∠BAO+∠OBA=90°，∠OBA+∠EBG=90°，

∴∠BAO=∠EBG，

在△BAO和△EBG中，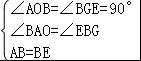

∴△BAO≌△EBG（AAS），

∴BG=AO，EG=OB，

∵OB=BF，

∴BF=EG，

在△EGP和△FBP中，，

∴△EGP≌△FBP（AAS），

∴PB=PG，

∴PB=BG=AO=3

即：PB的长度不发生改变，是定值为3．

【点评】此题是三角形综合题，主要考查了勾股定理、角平分线的性质、全等三角形的判定与性质，熟练掌握三角形全等的证明是解本题的关键．