八年级（上）期末数学试卷集（305题）

---

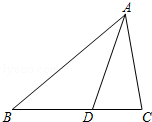
如图，在△ABC中，∠B=42°，∠C=78°，AD平分∠BAC．

（1）求∠ADC的度数；

（2）在图中画出BC边上的高AE，并求∠DAE的度数．

 

知识点：试卷03

参考答案：见解析

解析：

【分析】（1）根据三角形的内角和得到∠BAC=180°﹣∠B﹣∠C=60°，由角平分线的性质得到∠BAD=∠BAC=30°，根据三角形的外角的想自己看得到结论；

（2）过A作AE⊥BC于E，根据垂直的定义得到∠AEB=90°，根据三角形的外角的性质即可得到结论．

【解答】（1）∵∠B=42°，∠C=78°，

∴∠BAC=180°﹣∠B﹣∠C=60°，

∵AD平分∠BAC，

∴∠BAD=∠BAC=30°，

∴∠ADC=∠B+∠BAD=42°+30°=72°；

 

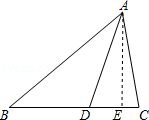
（2）如图所示，过A作AE⊥BC于E，

∴∠AEB=90°，

∴∠DAE=180°﹣∠AED﹣∠ADE=180°﹣90°﹣72°=18°．

 

【点评】本题考查了三角形的内角和，角平分线的定义，熟记三角形的内角和是解题的关键．