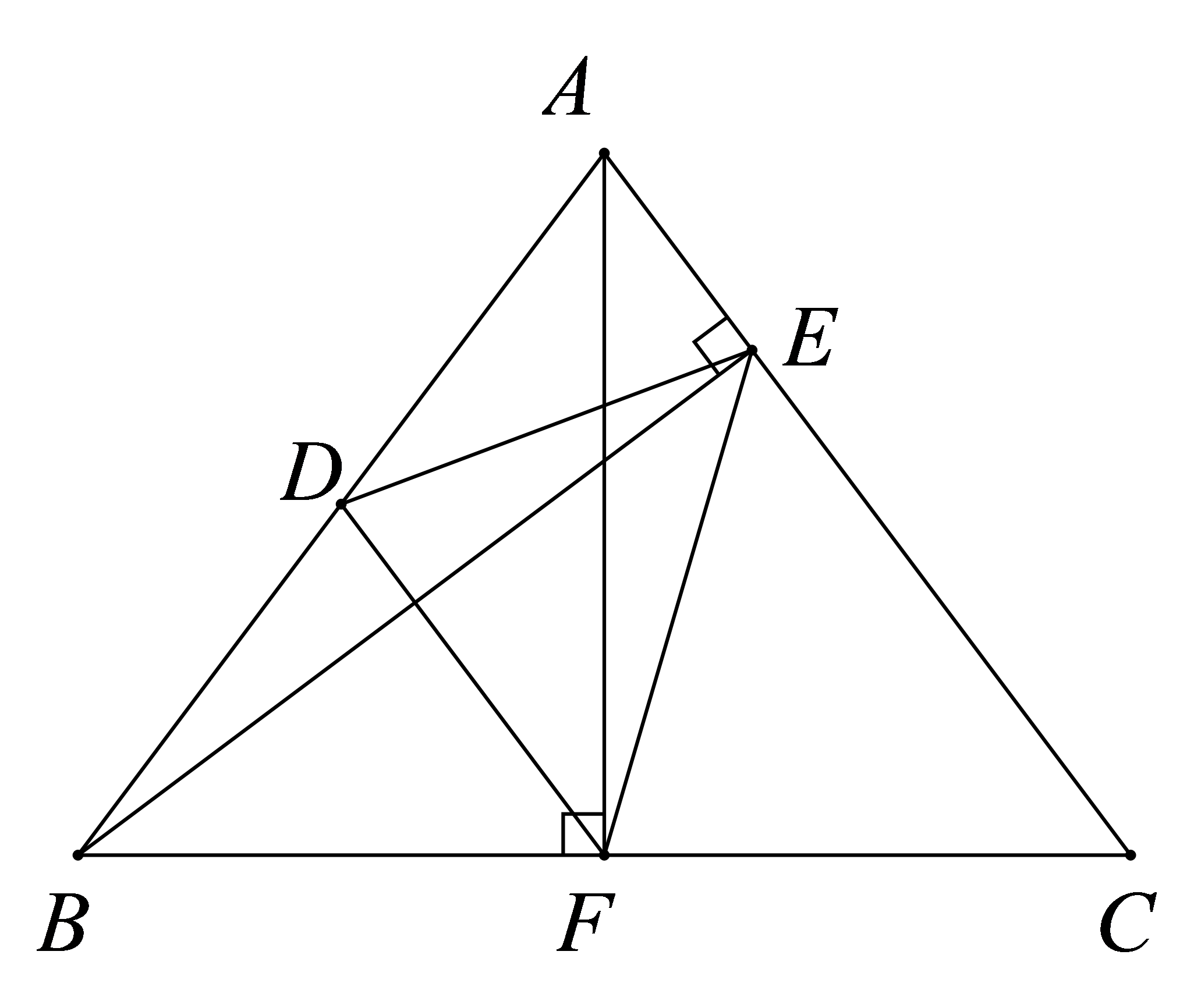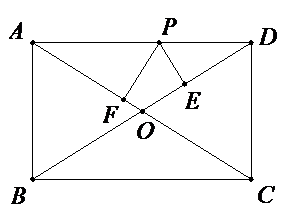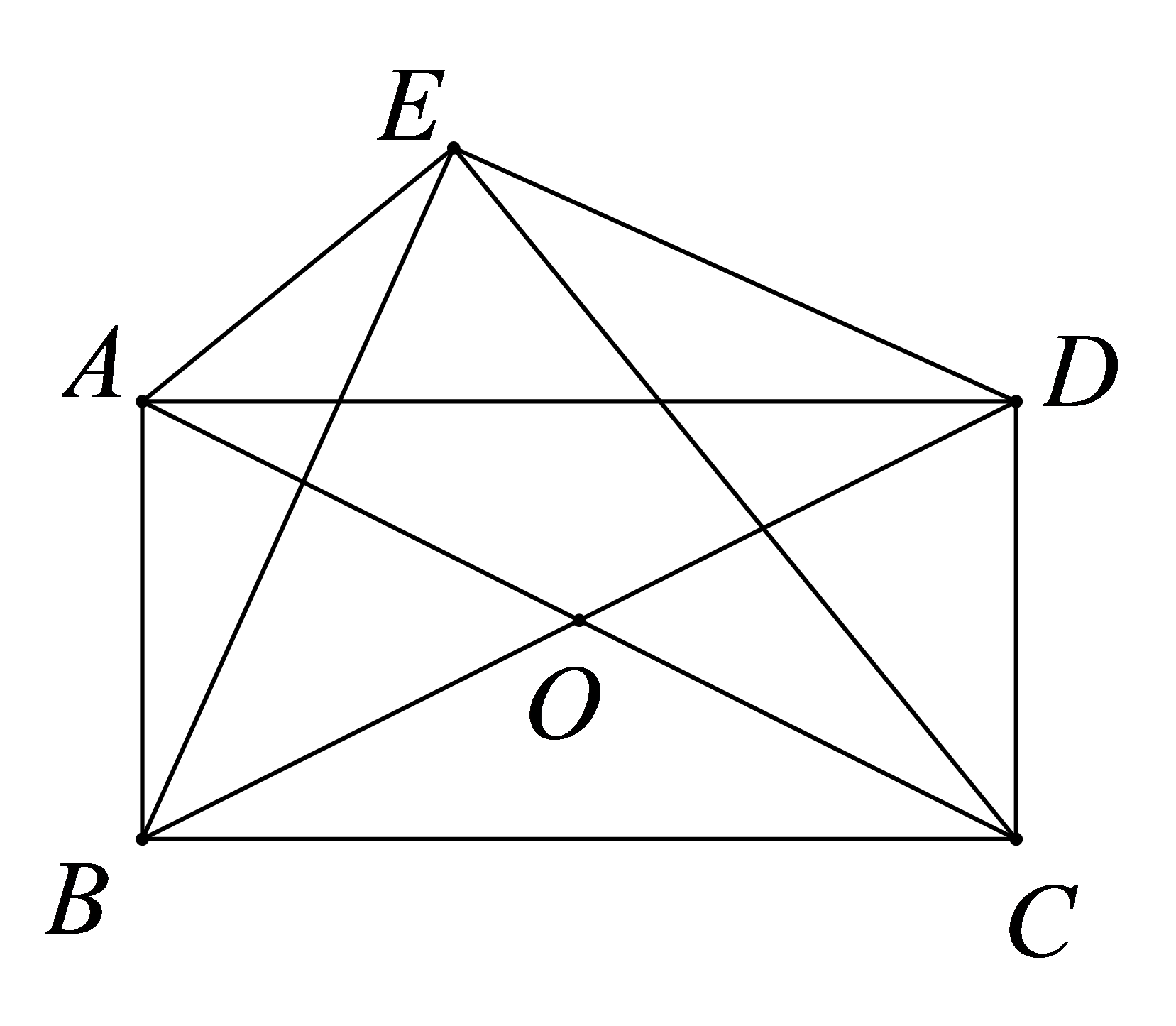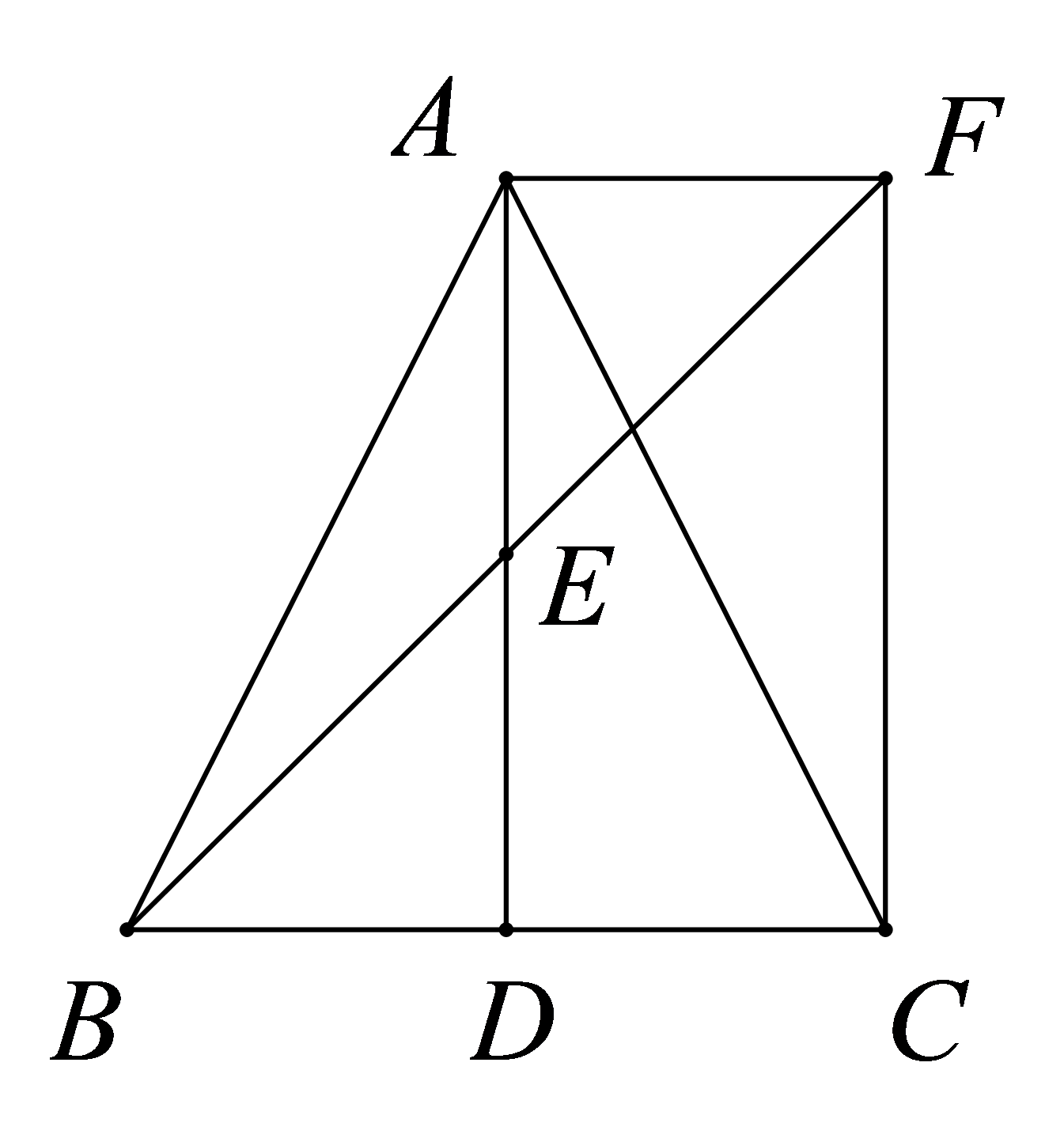“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
第321题
如图,在矩形\( ABCD\)中,\( AC\mathrm{、}BD\)交于点\( O\),若\(AB=5\),\(AC=13\),求\( △BOC\)的周长。 
参考答案:∵矩形\( ABCD\),\(AC=13\)
\(\therefore \mathrm{\angle }ABC=90°\),
\(AC=BD\),\( AC\)与\( BD\)互相平分
\(\therefore OB=OC=\frac {1} {2}AC=6.5\)
\( \because \)在\( \mathrm{R}\mathrm{t}△ABC\)中,
\(AB=5\),\(AC=13\),\(\mathrm{\angle }ABC=90°\)
∴\(A{B^2} + B{C^2} = A{C^2}\)
\(\therefore BC=\sqrt {{{13}^{2}}-{{5}^{2}}}=12\)
\( \therefore △BOC\)周长为:\( BC+OB+OC=25\)
参考答案:\(\sqrt 3 + 1\)
第323题
如图,矩形 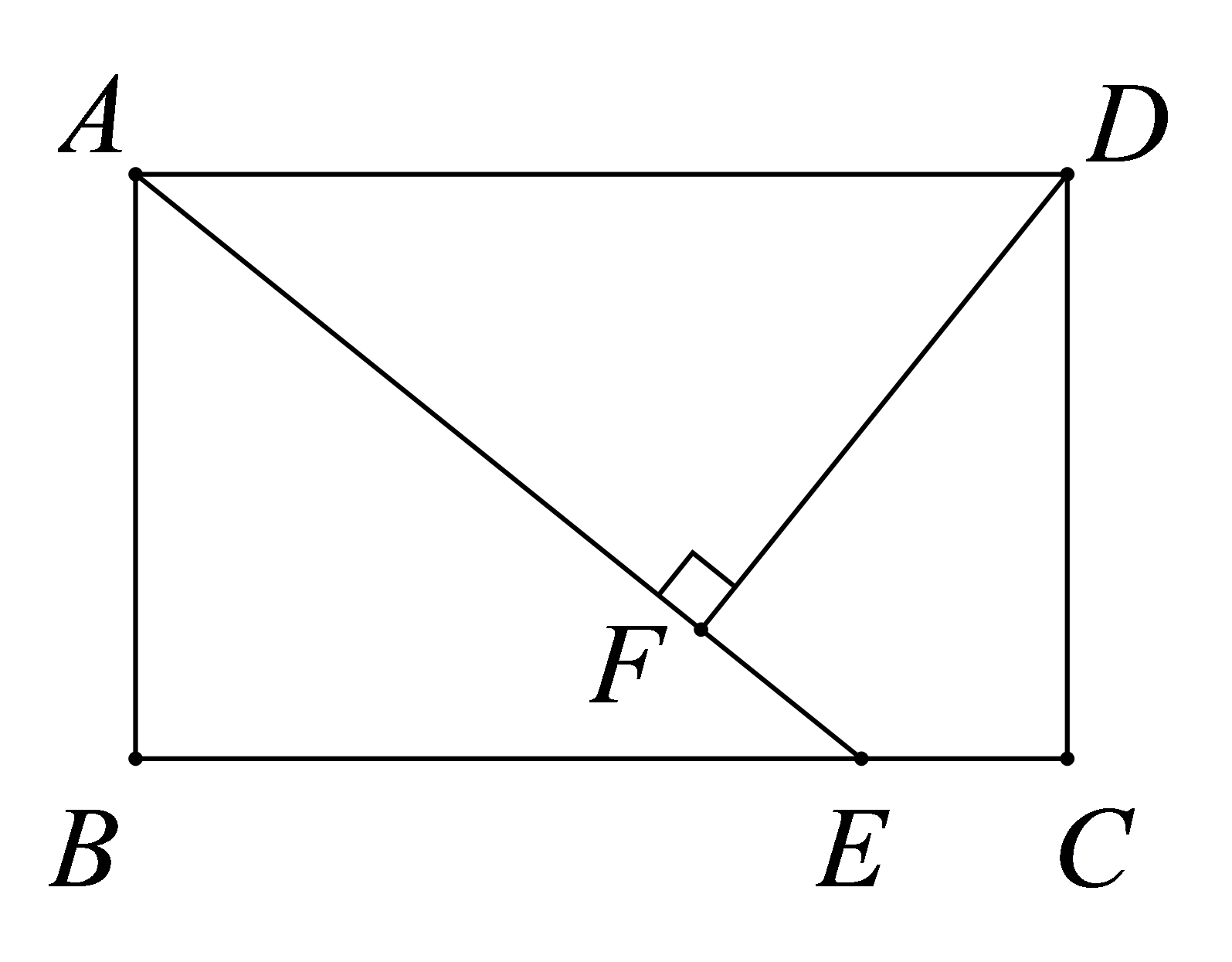
参考答案:
证明:∵四边形
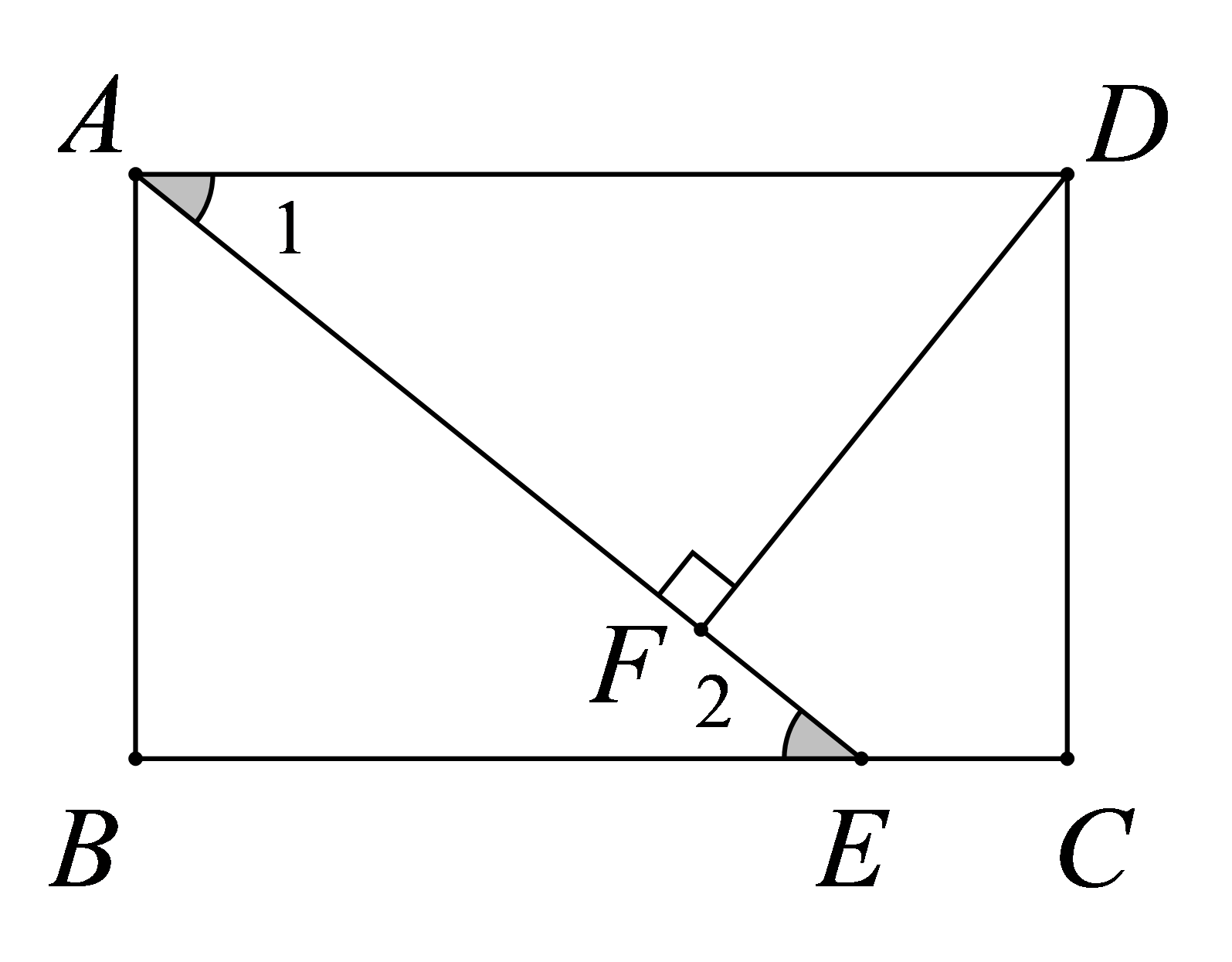
∵
又∵
∴
∴△
∴
∴
A.3
B.\(\sqrt 7 \)
C.\(\sqrt 6 \)
D.4
参考答案:D
参考答案:\( BO=BE\)
证明:∵矩形\( ABCD\)
\(\therefore \mathrm{\angle }BAD\)
\(=\mathrm{\angle }ABC=90°\),
\( AC\)与\( BD\)互相平分且\(AC=BD\)
\(\therefore OA=OB\)
\( \because AE\)平分\( \mathrm{\angle }BAD\)
\(\therefore \mathrm{\angle }BAE=45°\)
\(\because \mathrm{\angle }EAC=15°\)
\(\therefore \mathrm{\angle }BAO=60°\)
\( \therefore △ABO\)是等边三角形
\(\therefore BO=AB\)
\(\because \mathrm{\angle }BAE=45°\),
\(\mathrm{\angle }ABE=90°\)
\(\therefore \mathrm{\angle }AEB=45°\)
\(=\mathrm{\angle }BAE\)
\(\therefore BE=AB\)
\(\therefore BO=BE\)
第326题
求证:\( BF=DF\);
参考答案:证明:
\( \because \mathrm{ }△BCD\)沿对角线\( BD\)折叠得到\( △BFD\),
\( \therefore \mathrm{\angle }DBC\)
\(=\mathrm{\angle }DBE\mathrm{ }\)
∵ 矩形\( ABCD\)中,\( AD//BC\)
\( \therefore \mathrm{ }\mathrm{\angle }DBC\)
\(=\mathrm{\angle }ADB\)
\( \therefore \mathrm{ }\mathrm{\angle }ADB\)
\(=\mathrm{\angle }DBE\)
\( \therefore \mathrm{ }BF=DF\)
第327题
若
参考答案:解:由(1)设\(BF=x=DF\),
∵矩形\( ABCD\),\(BC=8\)
\(\therefore \mathrm{\angle }BAD=90°\),\(AD=BC=8\)
\(\therefore AF=8-x\),
∵在\( \mathrm{R}\mathrm{t}△ABF\)中,\(AB=4\),\(\mathrm{\angle }BAF=90°\)
∴\(A{B^2} + A{F^2} = B{F^2}\)
∴\({4^2} + {\left( {8 - x} \right)^2} = {x^2}\)
解得:\(x=5\)
\(\therefore \mathrm{}BF=5\)
参考答案:
证明:连接
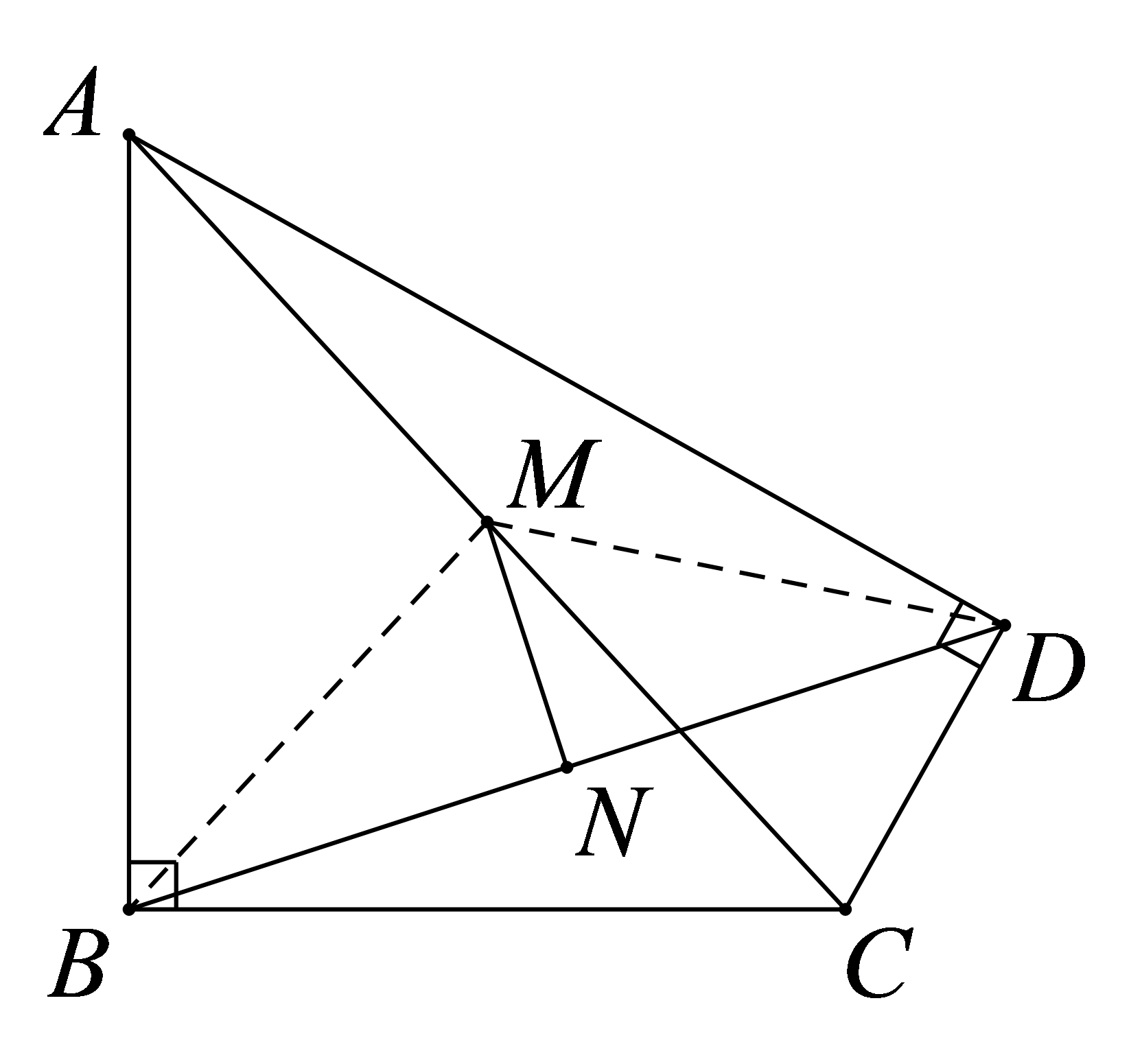
∵点
参考答案:
连结
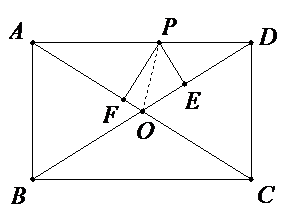
∵由矩形
而
即
参考答案:\( \mathrm{\angle }ABC=90°\)
参考答案:\(\frac{{24}}{5}\)
参考答案:符合;两组对边分别相等的四边形为平行四边形;勾股逆定理;有一个角为直角的平行四边形是矩形。
A.\(2\sqrt 5 \)
B.\(\sqrt 5 \)
C.3
D.4
参考答案:A
参考答案:证明:\(\because AF//BC\)
\(\therefore \angle AFE = \angle DBE\)
\(\because E\)是线段\(AD\)的中点
\(\therefore AE = DE\)
\(\because \angle AEF = \angle DEB\)
\(\therefore \Delta BDE\cong \Delta FAE(\text{AAS})\)
\(\therefore AF = BD\)
\(\because D\)是线段\(BC\)的中点
\(\therefore BD = CD\)
\(\therefore AF = CD\)
\(\because AF//CD\)
\(\therefore \)四边形\(ADCF\)是平行四边形
\(\because AB = AC\)
\(\therefore AD \bot BC\)
\(\therefore \angle ADC = 90^\circ \)
\(\therefore \)平行四边形\(ADCF\)为矩形
参考答案:证明:
\(\because D\),\(E\),\(F\)分别是\(AC\),\(AB\),\(BC\)的中点
\(\therefore DE\)、\(EF\)分别是\(\Delta ABC\)的中位线
\(\therefore DE//BC\),\(EF//AC\)
\(\therefore \)四边形\(DEFC\)是平行四边形
\(\because \angle C = 90^\circ \)
\(\therefore \)平行四边形\(DEFC\)是矩形
第337题
如图,平行四边形\( ABCD\)中,\(∠1=∠2\),求证:四边形\( ABCD\)是矩形。
参考答案:证明:\(∵∠1=∠2\)
\( \therefore OA=OB\)
∵四边形\( ABCD\)是平行四边形
\(\therefore AC=2OA,BD=2OB\)
\(\therefore AC=BD\)
∴平行四边形\( ABCD\)是矩形
参考答案:证明:
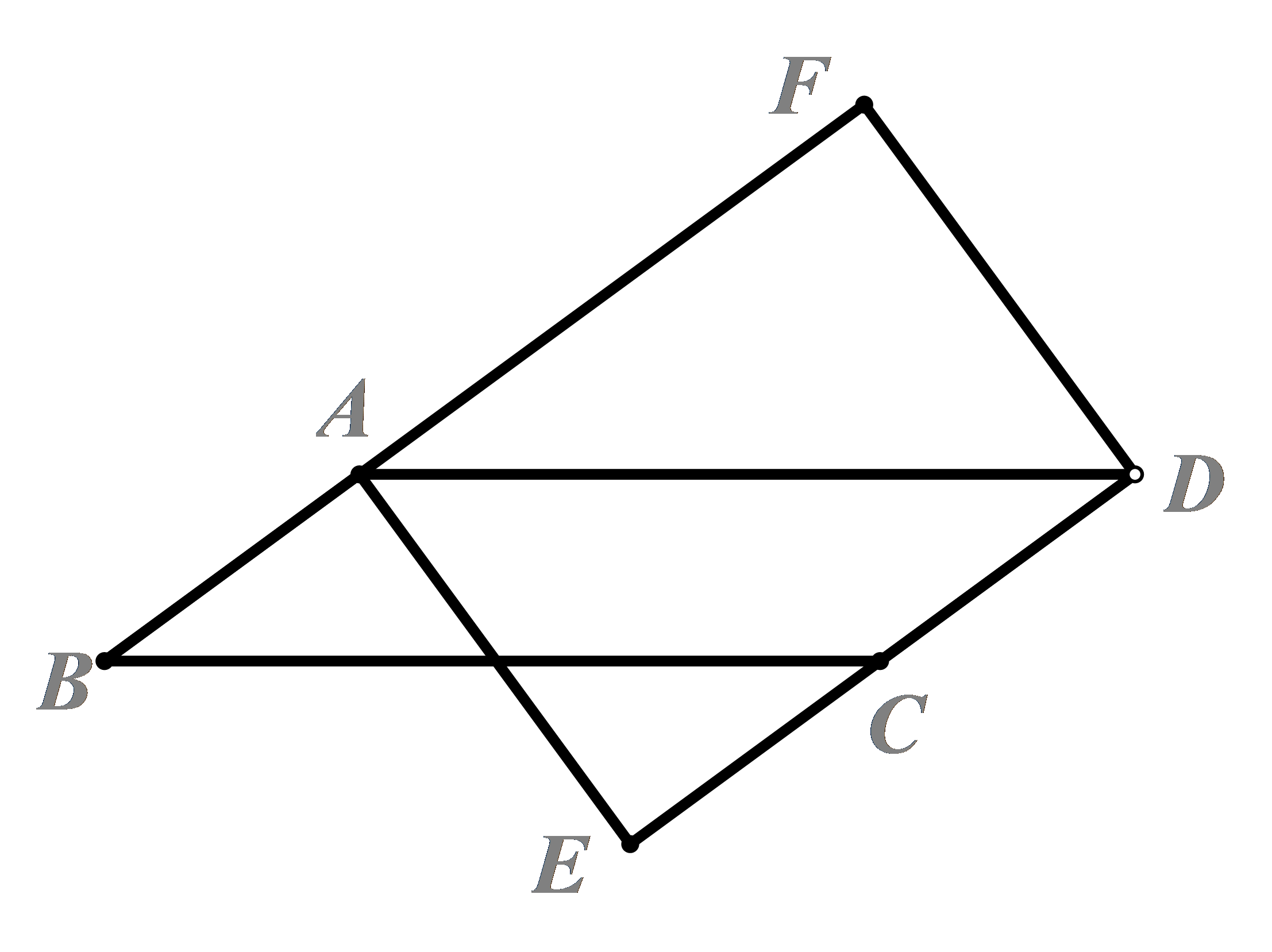
\(\because AB = AC\),
\(AD\)平分\(\angle BAC\),
\(\therefore AD \bot BC\),
\(\angle CAD = \frac{1}{2}\angle BAC\),
\(\therefore \angle ADC = 90^\circ \)。
\(\because AN\)是\(\Delta ABC\)外角的平分线,
\(\therefore \angle CAE \)
\(= \frac{1}{2}\angle CAM\)。
\(\because \angle BAC + \angle CAM \)
\(= 180^\circ \),
\(\therefore \angle DAN \)
\(= \angle CAD + \angle CAE\)
\( = \frac{1}{2}(\angle BAC + \angle CAM) \)
\(= 90^\circ \)。
\(\because CE \bot AN\),
\(\therefore \angle CEA = 90^\circ \),
\(\therefore \)四边形\(ADCE\)为矩形。
第339题
如图,在平行四边形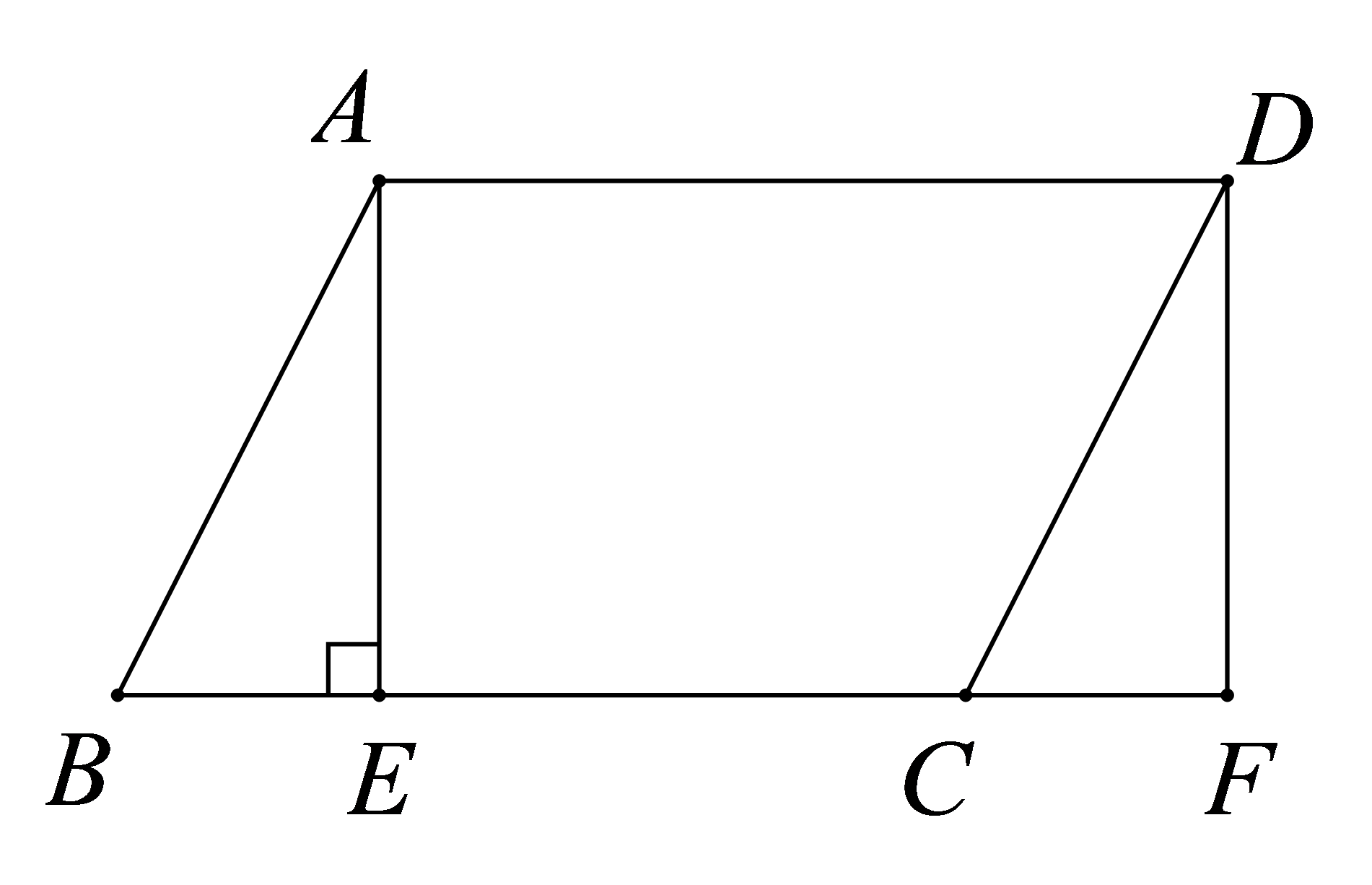
参考答案:证明:
\(\because CF = BE\),
\(\therefore CF + EC = BE + EC\).即\(EF = BC\),
\(\because \)四边形\(ABCD\)是平行四边形,
\(\therefore AD//BC\),\(AD = BC\),
\(\therefore AD//EF\),\(AD = EF\),
\(\therefore \)四边形\(AEFD\)是平行四边形。
\(\because AE \bot BC\),
\(\therefore \angle AEF = 90^\circ \).
\(\therefore \)平行四边形\(AEFD\)是矩形。
参考答案:证明:\(\because \)四边形\(ABCD\)是平行四边形,
\(\therefore AB//DC\),\(AF//ED\),
\(\because AE \bot DC\),
\(∴AE⊥BA\),
∵\(DF \bot BA\),
\(\therefore DF//EA\),
\(\therefore \)四边形\(AEDF\)是平行四边形,
\(\because AE \bot DE\),
\(\therefore \angle E = 90^\circ \),
\(\therefore \)四边形\(AEDF\)是矩形。