初中数学八年级下册（648题）

---

如图，\(\Delta ABC\)中，\(AB = AC\)，\(AD\)平分\(\angle BAC\)，射线\(AN\)平分外角\(\angle CAM\)，过点\(C\)作\(CE \bot AN\)于点\(E\)，求证：四边形\(ADCE\)是矩形。

    

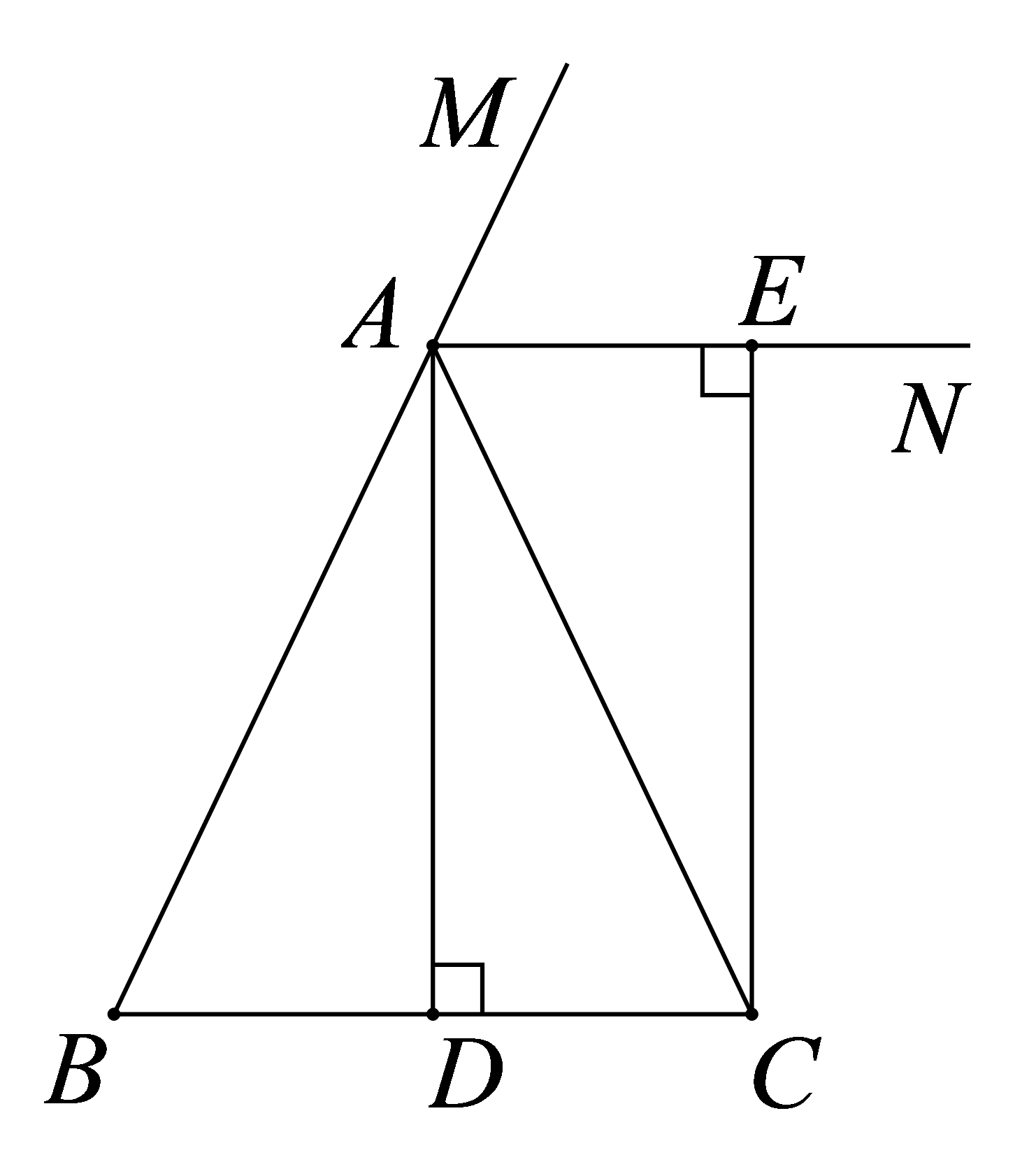
知识点：第十八章　平行四边形

参考答案：证明：
\(\because AB = AC\)，
\(AD\)平分\(\angle BAC\)，
\(\therefore AD \bot BC\)，
\(\angle CAD = \frac{1}{2}\angle BAC\)，
\(\therefore \angle ADC = 90^\circ \)。
\(\because AN\)是\(\Delta ABC\)外角的平分线，
\(\therefore \angle CAE \)
\(= \frac{1}{2}\angle CAM\)。
\(\because \angle BAC + \angle CAM \)
\(= 180^\circ \)，
\(\therefore \angle DAN \)
\(= \angle CAD + \angle CAE\)
\( = \frac{1}{2}(\angle BAC + \angle CAM) \)
\(= 90^\circ \)。
\(\because CE \bot AN\)，
\(\therefore \angle CEA = 90^\circ \)，
\(\therefore \)四边形\(ADCE\)为矩形。