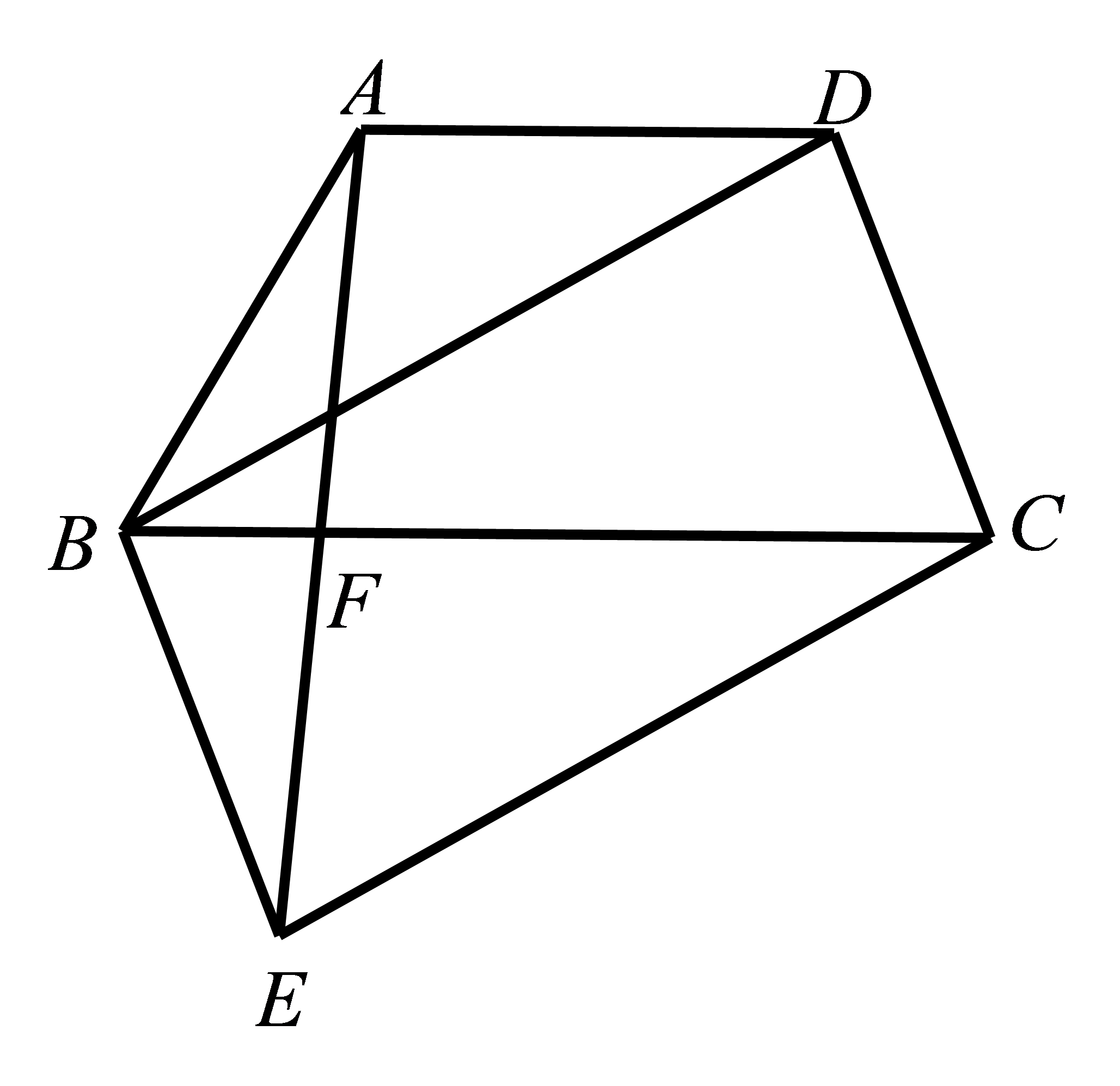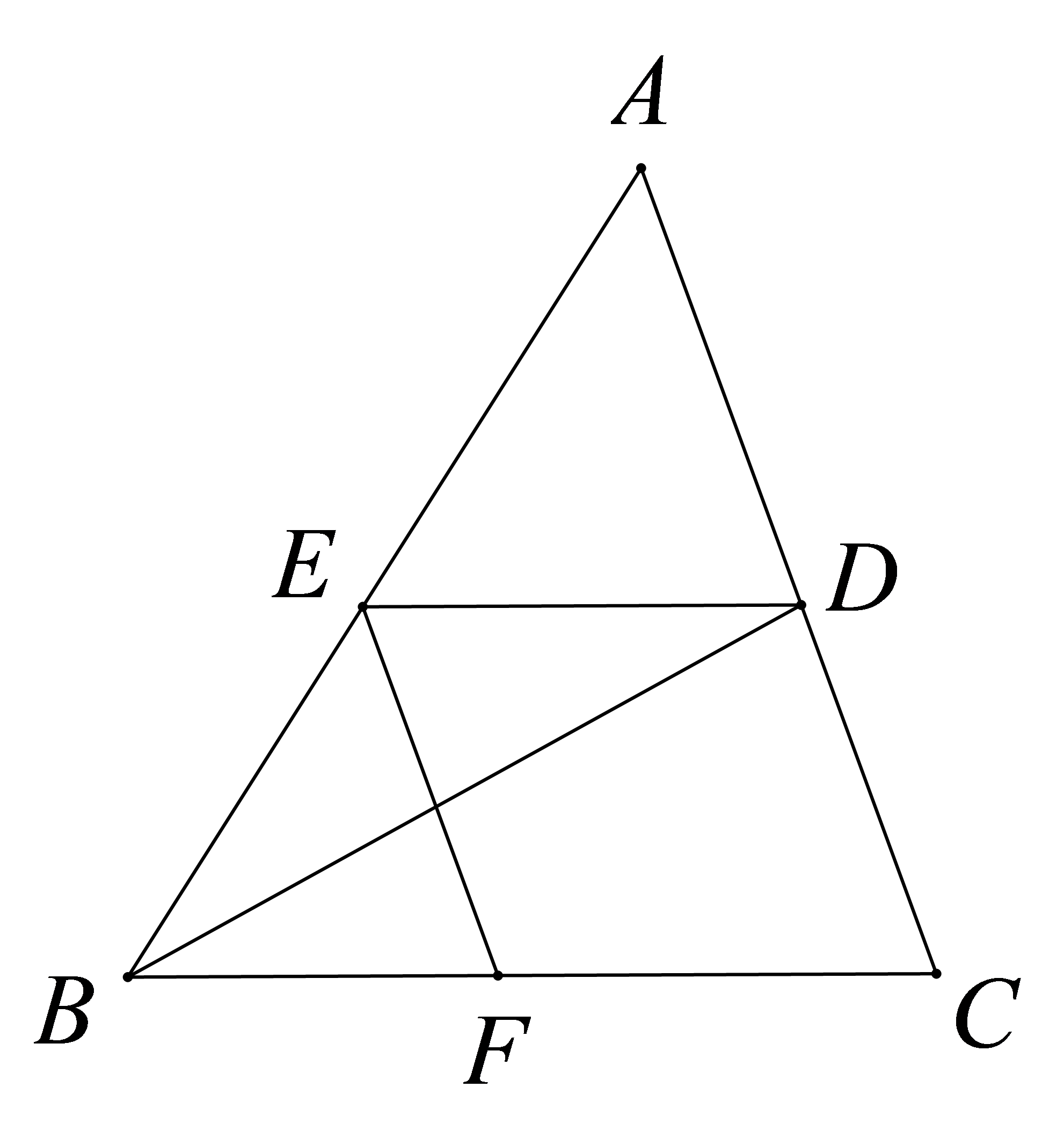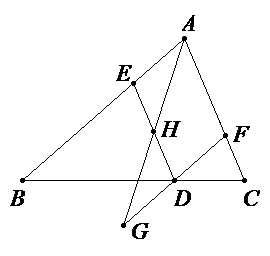第281题

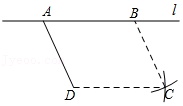
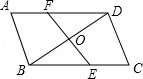
如图，\( E\)是\(▱ABCD\)的边\( AD\)延长线上一点，\( BE\)交\( DC\)于\( F\)。求证：\( {S}_{△ADF}＝{S}_{△EFC}\)。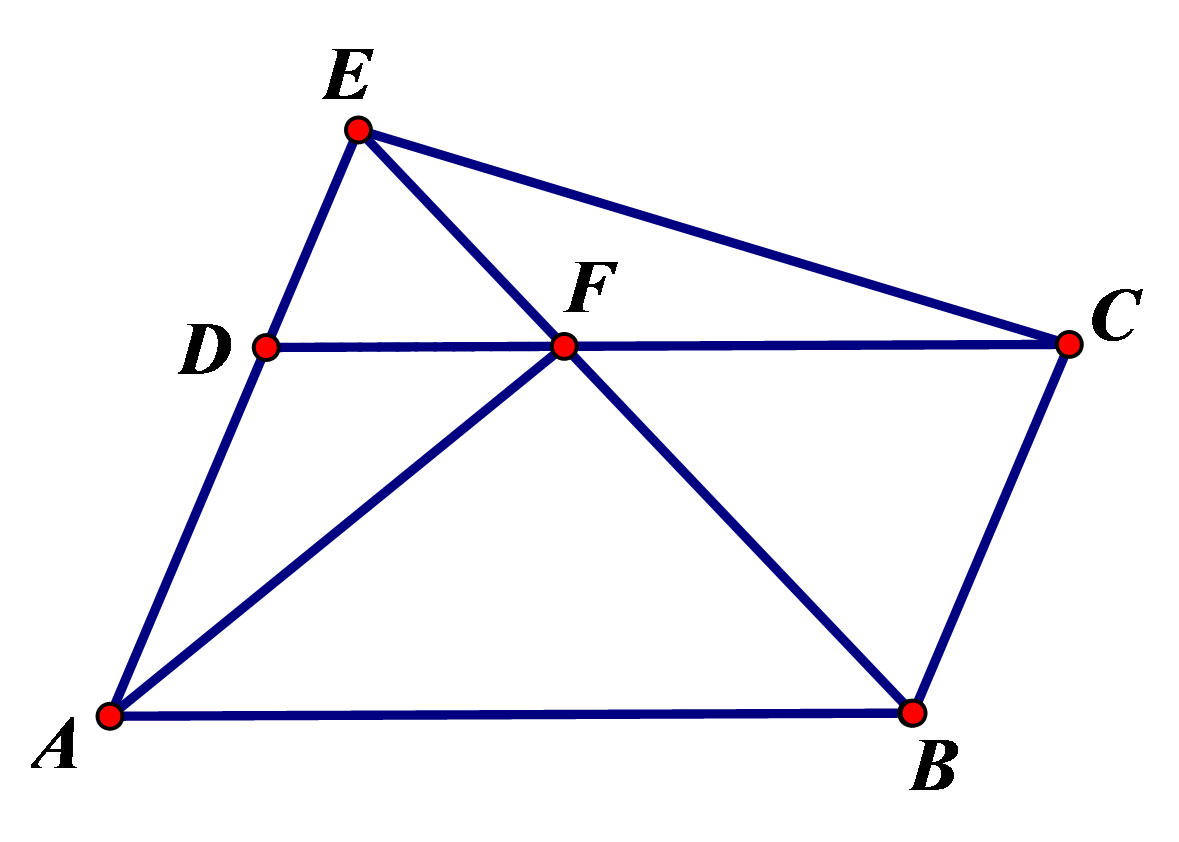

参考答案：\(\because ▱ABCD\mathrm{}，\)
\(\therefore AB//CD，AD//BC，\)
\(\therefore AB//CD，\mathrm{}AE//BC\mathrm{}\)

连接\( BD\)

\( \therefore {S}_{△BDF}＝{S}_{△ADF}，\)
\(\because {S}_{△BCE}＝{S}_{△BCD}，\)
\(\therefore {S}_{△CFE}＝{S}_{△BFD}，\)
\(\therefore {S}_{△FDB}＝{S}_{△FDA}\)。

第282题

A.\( AB=CD，AD=BC\)

B.\( AB//CD，AB=CD\mathrm{ }\)

C.\( AB=CD，AD//BC\)

D.\( AB//CD，AD//BC\)

参考答案：C

第283题

参考答案：是

第284题

参考答案：对边相等的四边形是平行四边形

第285题

参考答案：10

第286题

四边形\( ABCD\)，\( AD//BC\)，连接\( BD\)，过\( B\mathrm{、}C\)分别作\( CD\mathrm{、}BD\)的平行线交于\( E\)．连接\( AE\)交\( BC\)于\( F\)，求证：\( AF=EF\)。

参考答案：证明：
过点\( A\)作\( AM//CD\)交\( \mathrm{B}\mathrm{C}\)于\( M\)，连接\( EM\)
\( \because AM//DC\)，且\( AD//MC\)，
∴四边形\( AMCD\)为平行四边形，
\( \therefore \mathrm{ }AM=CD\)且\( AM//CD\)。
又\( \because CD//BE，\mathrm{ }BD//CE\)，
∴四边形\( BECD\)为平行四边形，
\( \therefore CD//BE\)且\( CD=BE\)，
\( \therefore AM//BE\)且\( AM=BE\)，
∴四边形\( ABEM\)为平行四边形，
\( \therefore AF=EF\)。

第287题

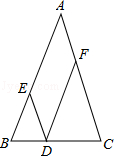
如图，在\(▱ABCD\)中，点\( E\)和\( F\)都在\( BD\)上，且\( BE＝DF\). 求证：四边形\( AECF\)是平行四边形。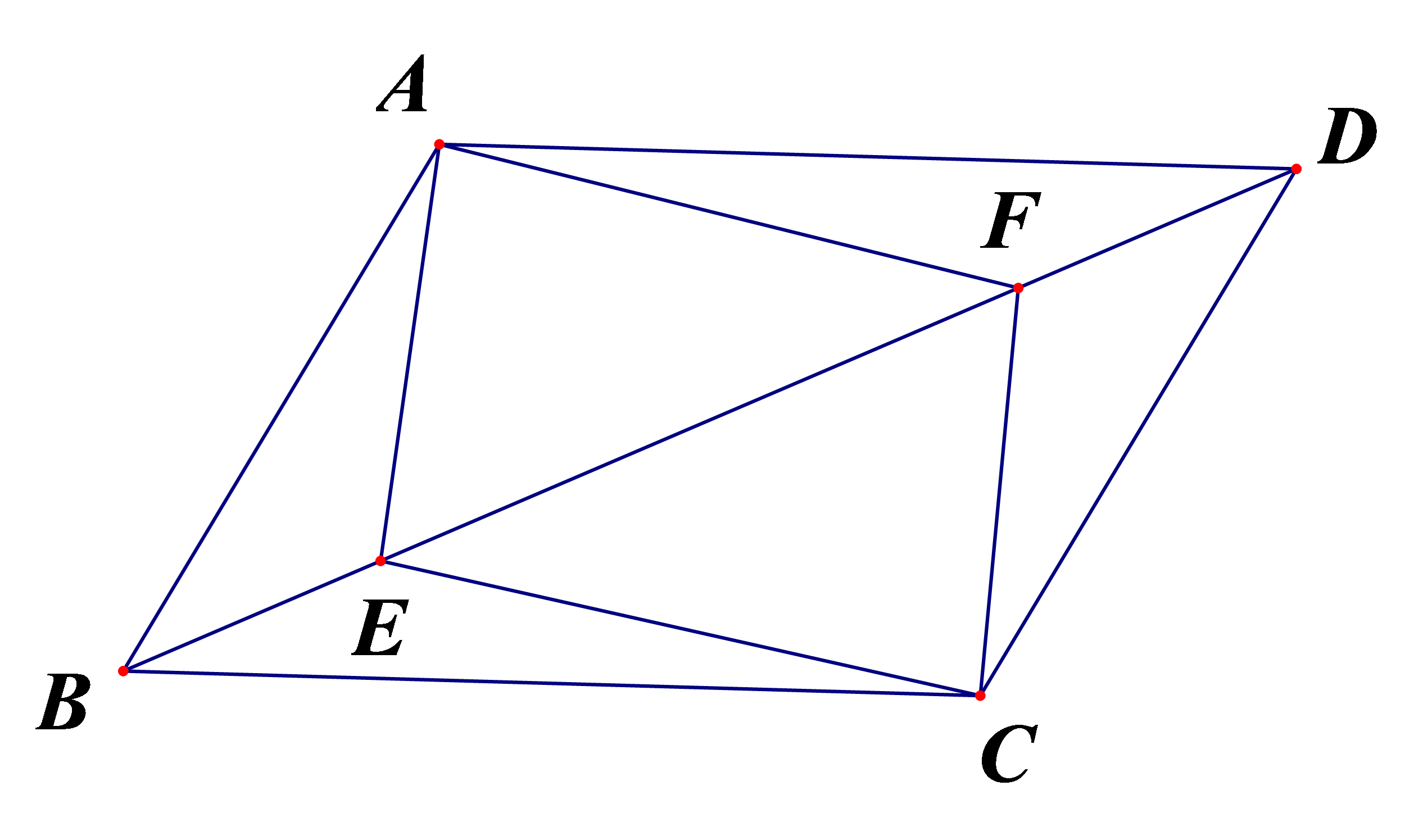

参考答案：证明：连接\( AC\)，令\( AC\)与\( BD\)交于点\( O\)
∵四边形\( ABCD\)为平行四边形，
\( \therefore AO=\mathrm{ }CO，BO=\mathrm{ }DO\)
\( \because BE＝DF，\therefore EO=FO\)
又\( \because AO=\mathrm{ }CO，\)
∴四边形\( AECF\)为平行四边形。

第288题

如图， 在\( △ABC\)中，\( BD\)平分\( \mathrm{\angle }ABC\)交\( AC\)于点\( D\)，\( DE//BC\)交\( AB\)于点\( E\)，\( EF//AC\)交\( BC\)于点\( F\). 求证：\( BE＝CF\)。

参考答案：证明：
∵\( BD\)平分\( \mathrm{\angle }ABC，\)
\(\therefore \mathrm{\angle }ABD=\mathrm{\angle }DBC\)
\( \because DE//BC，\)
\(\therefore \mathrm{\angle }EDB=\mathrm{\angle }DBC，\)
\(\therefore \mathrm{\angle }EDB=\mathrm{\angle }ABD，\)
\(\therefore △EBD\)为等腰三角形，
\( \therefore EB=ED\)。
又\( \because DE//BC，EF//AC，\)
∴四边形\( EFCD\)为平行四边形，
\( \therefore CF=ED，\)
\(\therefore CF=BE\)。

第289题 能判定四边形\(ABCD\)是平行四边形的条件是\(∠A：∠B：∠C：∠D\)的值为（    ）

A.1：2：3：4

B.1：4：2：3

C.1：2：2：1

D.1：2：1：2

参考答案：D

第290题 能判定四边形\(ABCD\)是平行四边形的题设是（    ）

A.\(AD=BC\)，\(AB//CD\)

B.\(∠A=∠B\)，\(∠C=∠D\)

C.\(AB=BC\)，\(AD=DC\)

D.\(AB//CD\)，\(CD=AB\)

参考答案：D

第291题

如图，在\(▱ABCD\)中，\(E，F\)分别是边\(AB，CD\)上的点. 已知\(AE=CF\)，\(M，N\)分别为\(DE，BF\)的中点. 求证：四边形\(ENFM\)是平行四边形。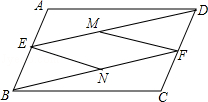

参考答案：证明：
\(∵▱ABCD\)，
\(∴AB//CD，AB=CD\)，
\(∵AE=CF，∴BE=DF，BE//DF\)。
∴四边形\(BEDF\)为平行四边形。
\(∴DE//BF，DE=BF\)，
\(∵M，N\)分别为\(DE，BF\)的中点，
\(∴EM//NF，EM=NF\)，
∴四边形\(ENFM\)是平行四边形。

第292题

如图，在四边形\(ABCD\)中，\(AB=DC，AD=BC\)，点\(E\)在\(BC\)上，点\(F\)在\(AD\)上，\(AF=CE\)，\(EF\)与对角线\(BD\)相交于点\(O\)，求证：\(O\)是\(EF\)的中点。

参考答案：证明：
\(∵AB=DC\)，\(AD=BC\)，
∴四边形\(ABCD\)为平行四边形
\(∴AD//BC，AD=BC\)，
∵点\(E\)在\(BC\)上，点\(F\)在\(AD\)上，\(AF=CE\)，
\(∴FD=BE\)且\(FD//BE\) ，
∴连接\(FB，ED\)，四边形\(EBFD\)为平行四边形
∵对角线\(EF\)与对角线\(BD\)相交于点\(O\)，
\(∴O\)是\(EF\)的中点。

第293题

已知：如图，\(△ABC\)中，\(D、E、F\)分别在边\(BC、AB、AC\)上，且\(DE//AC，DE=AF\)，延长\(FD\)至点\(G\)，使\(DG=DF\)，连结\(AG\)交\(DE\)于点\(H\)。求证：\(HE=HD\)。

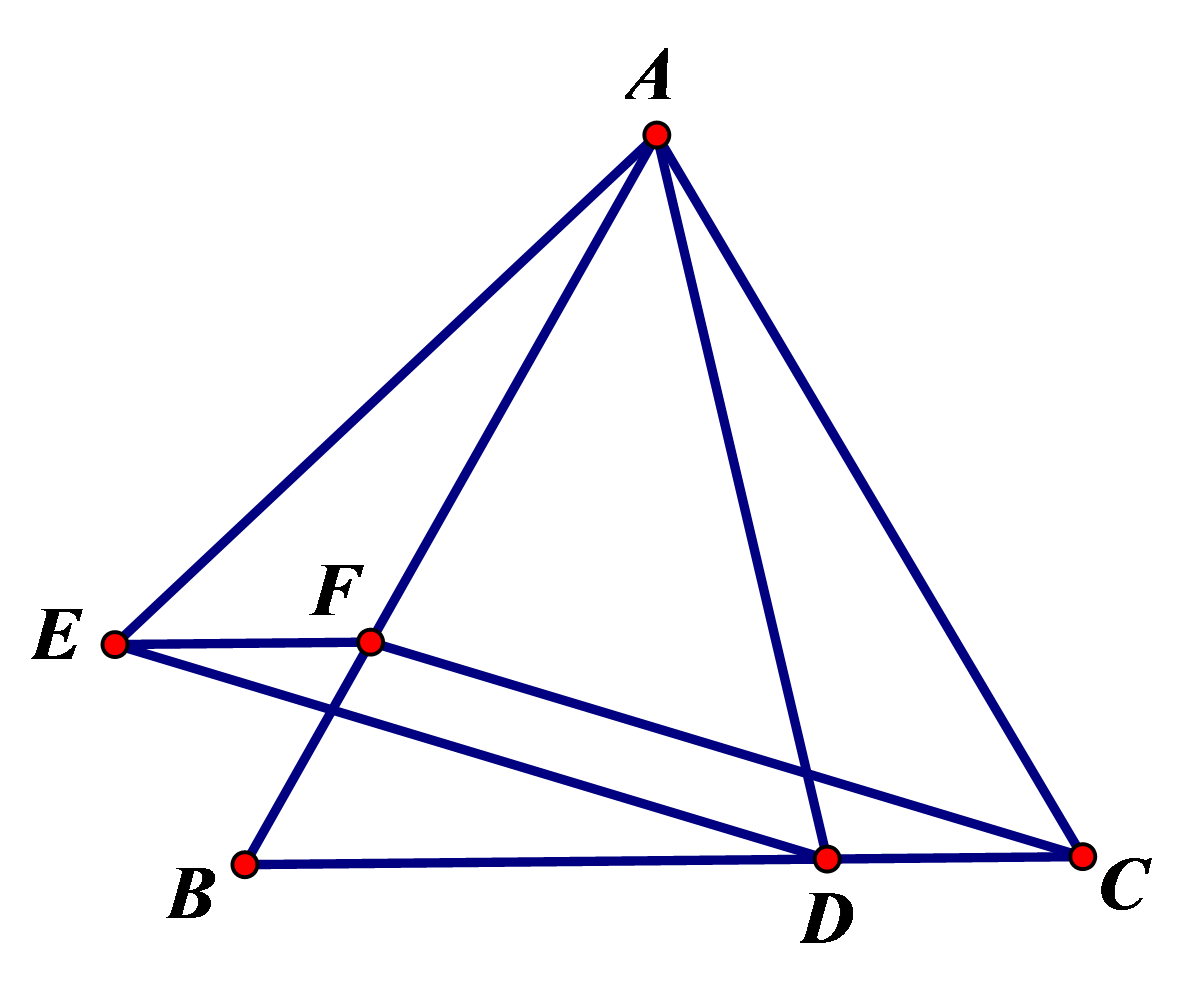
参考答案：证明：
\(∵DE//AC，DE=AF\)，
\(∴AEDF\)为平行四边形，
\(∴FD//AE，FD=AE\)
\(∵DG=DF，\)
\(∴DG=AE，DG//AE\)，
\(∴\)连接\(EG，AD\)，
\(AEGD\)为平行四边形
\(∴AG\)交\(DE\)于点\(H\)，
\(∴HE=HD\)。

第294题

如图，在等边\(△ABC\)中，\(D、F\)分别为\(CB、BA\)上的点，且\(CD=BF\)，以\(AD\)为边作等边\(△ADE\)．使点\(E\)，点\(D\)分别落在\(AB\)边两侧。求证：四边形\(CDEF\)为平行四边形。

参考答案：证明：
∵等边\(△ABC\)，等边\(△ADE\)，
\(∴AD=AE，AB=AC，\)
\(∠EAD=∠BAC=60°\)

\(∴∠EAB=∠EAD-∠BAD\)
\(=∠BAC-∠BAD=∠DAC\)

∴连接\(BE\)，在\(△ADC\)和\(△AEB\)中，
\(AD=AE，∠DAC\)
\(=∠EAB，AC=AB\)

\(∴△ADC≌△AEB\left ( {\text{SAS}} \right )\)，
\(∴CD=EB，∠ABE\)
\(=∠ACB=60°\)

又因为\(CD=BF\)，
\(∴BE=BF\)，
\(∴△BEF\)为等边三角形
\(∴BF=EF，∠EFB=60°，\)
\(∴CD=EF，∠EFB=∠ABC\)
\(∴CD//EF\)，
∴四边形\(CDEF\)为平行四边形。

第295题

如图，四边形\(ABCD\)，\(AC，BD\)交于点\(O\)，\(AD//BC，∠BAD=∠BCD\). 求证：四边形\(ABCD\)是平行四边形。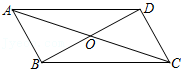

参考答案：证明：
\(∵AD//BC，
∴∠BAD+∠ABC\)
\(=∠BCD+∠ADC=180°\)
\(∵∠BAD=∠BCD\)，
\(∴∠ABC=∠ADC\)，
∴四边形\(ABCD\)为平行四边形。

第296题

如图，在\(▱ABCD\)中，对角线\(AC，BD\)相交于\(O，E，F\)是直线\(AC\)上两点，且\(AE=CF\)，求证：四边形\(BFDE\)是平行四边形。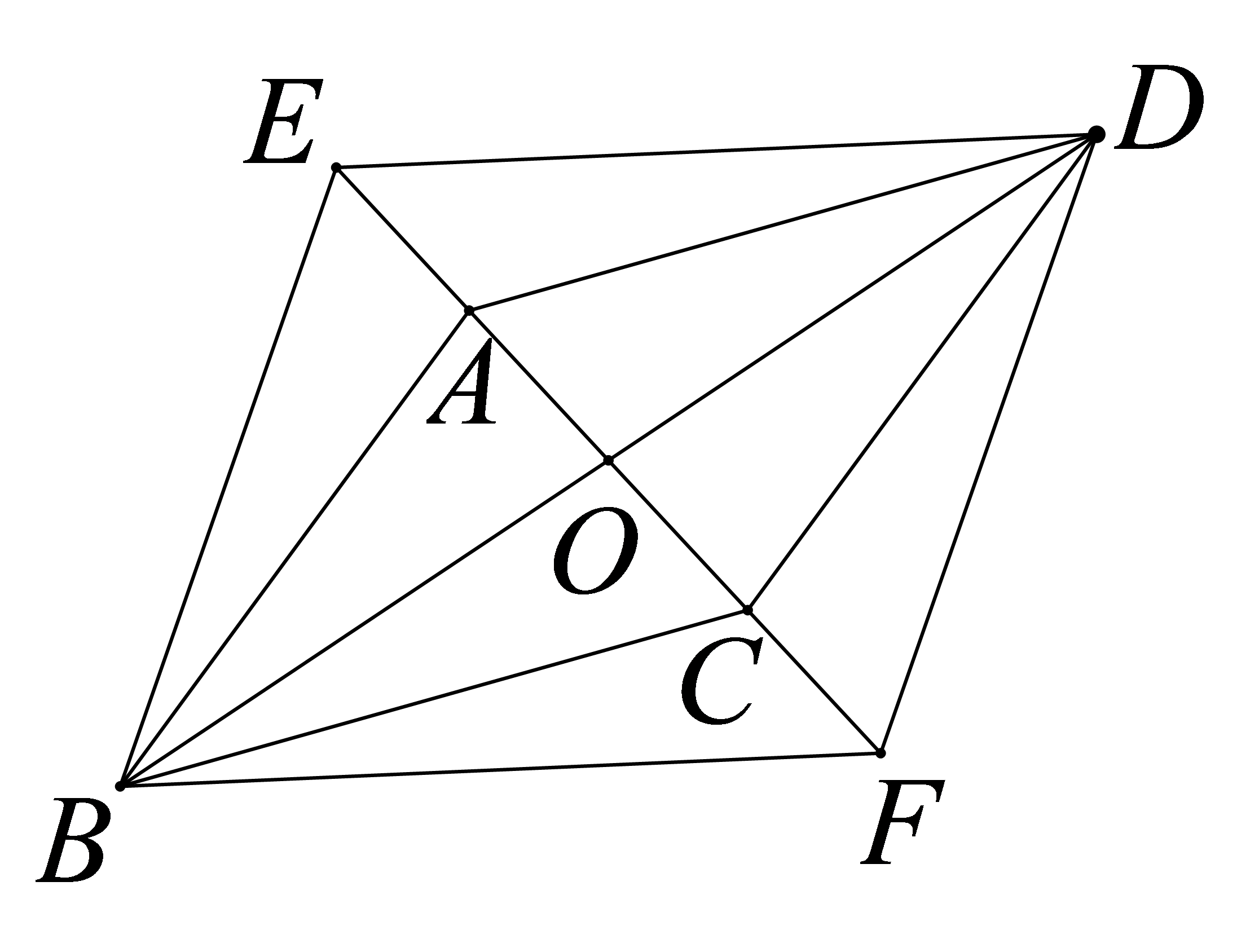

参考答案：证明：
\(∵▱ABCD，∴AO=CO，BO=DO\)，
\(∵AE=CF，∴EO=FO，∵BO=DO\)，
∴四边形\(BFDE\)为平行四边形。

第297题

四边形\(ABCD\)，\(∠A=∠C\)，下列条件中，增加___就可以判定四边形ABCD是平行四边形。

参考答案：①②

第298题 在四边形\(ABCD\)中，对角线\(AC\)和\(BD\)交于点\(O\)，\(BO=4，CO=6\)，当\(AO=\)___，\(DO=\)___时，这个四边形是平行四边形。

参考答案：6；4

第299题

如图，王老汉家中有一块平行四边形的地，地中有一口井\(P\)，王老汉的两个儿子要平均耕种这一块地，地界为一条线段且使这口井在地界上，你能帮助他们把地分开吗？简述作法，画出图形。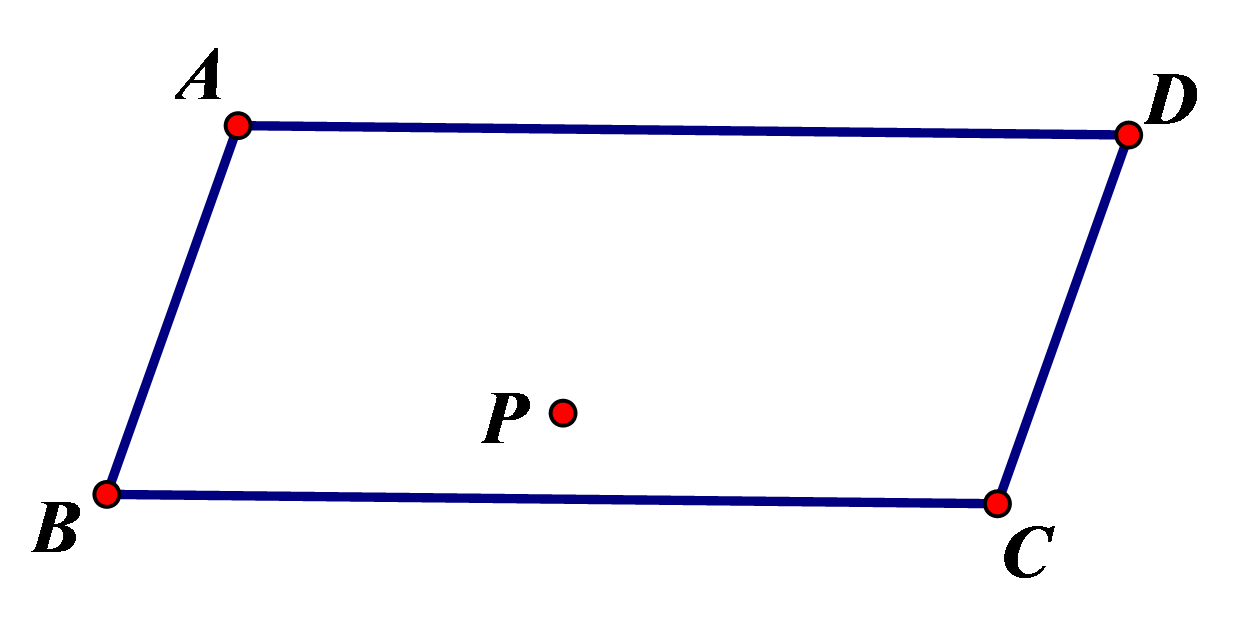

参考答案：可以，利用平行四边形的中心对称性，找到对称中心\(O\)，连接\(OP\)交\(AB，CD\)分别为\(N，M\)，线段\(NM\)即是地界

第300题 连接：___；

参考答案：\(FD\)或者\(FB\)