初中数学八年级下册（648题）

---

如图，在等边\(△ABC\)中，\(D、F\)分别为\(CB、BA\)上的点，且\(CD=BF\)，以\(AD\)为边作等边\(△ADE\)．使点\(E\)，点\(D\)分别落在\(AB\)边两侧。求证：四边形\(CDEF\)为平行四边形。

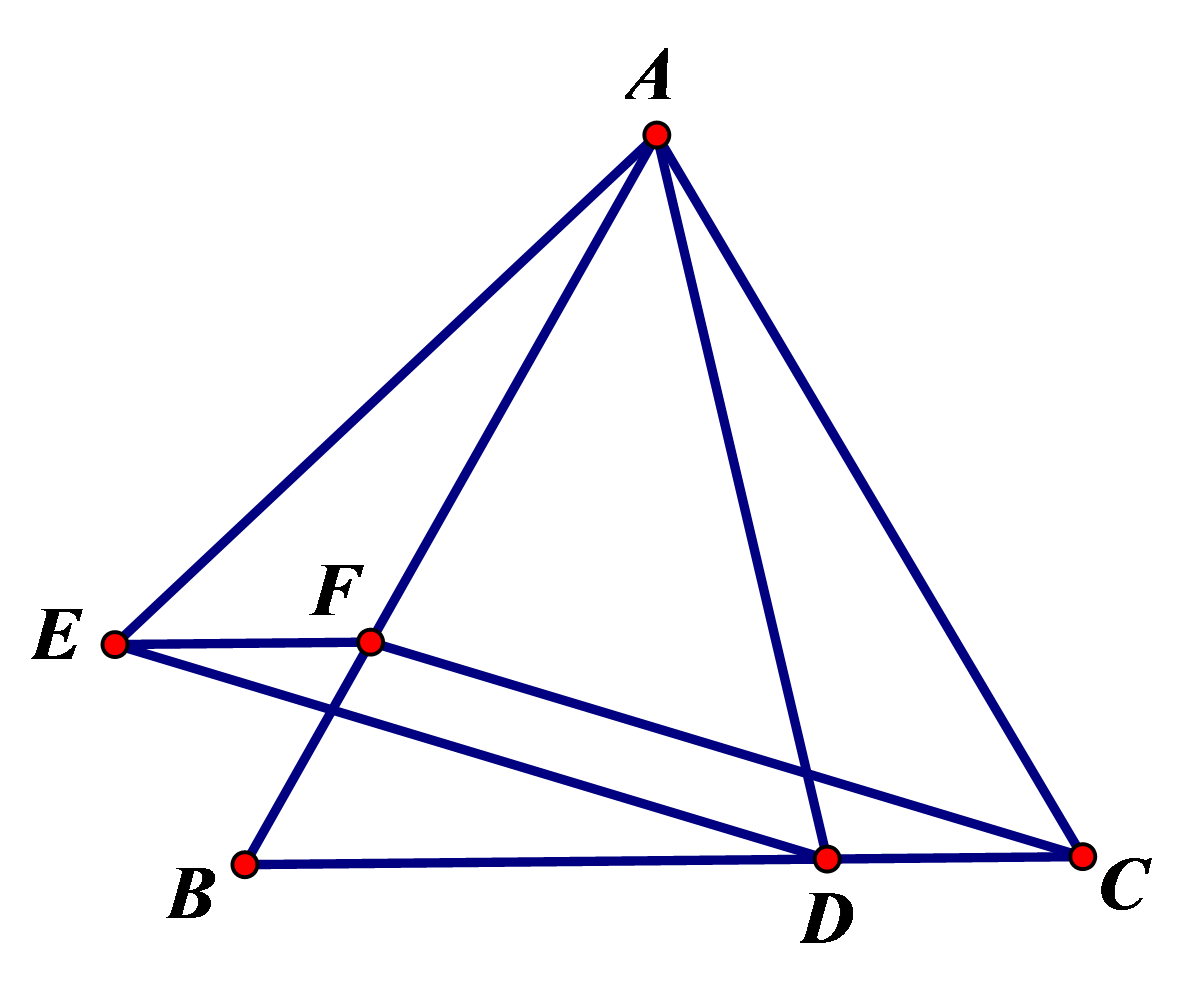
知识点：第十八章　平行四边形

参考答案：证明：
∵等边\(△ABC\)，等边\(△ADE\)，
\(∴AD=AE，AB=AC，\)
\(∠EAD=∠BAC=60°\)

\(∴∠EAB=∠EAD-∠BAD\)
\(=∠BAC-∠BAD=∠DAC\)

∴连接\(BE\)，在\(△ADC\)和\(△AEB\)中，
\(AD=AE，∠DAC\)
\(=∠EAB，AC=AB\)

\(∴△ADC≌△AEB\left ( {\text{SAS}} \right )\)，
\(∴CD=EB，∠ABE\)
\(=∠ACB=60°\)

又因为\(CD=BF\)，
\(∴BE=BF\)，
\(∴△BEF\)为等边三角形
\(∴BF=EF，∠EFB=60°，\)
\(∴CD=EF，∠EFB=∠ABC\)
\(∴CD//EF\)，
∴四边形\(CDEF\)为平行四边形。