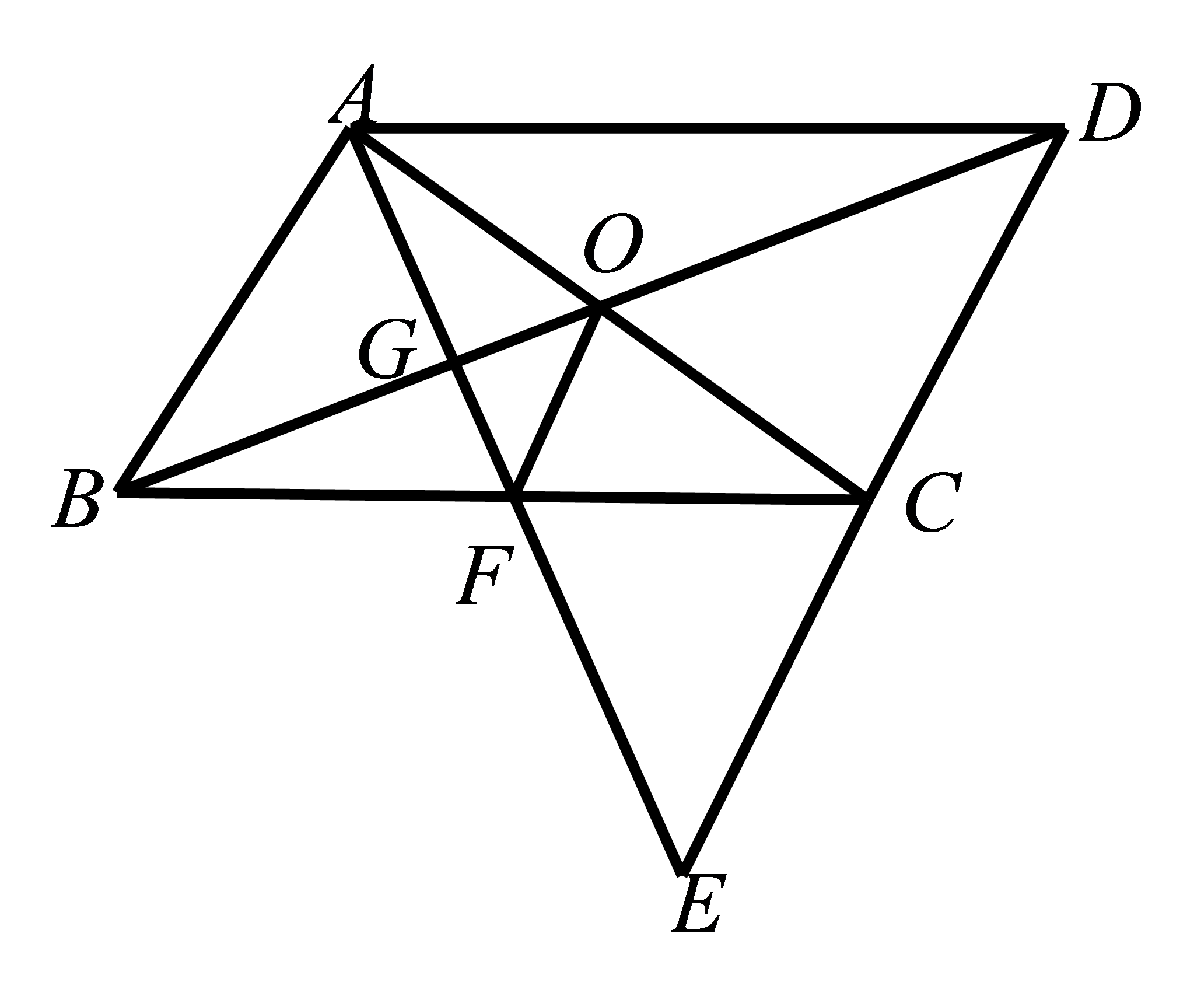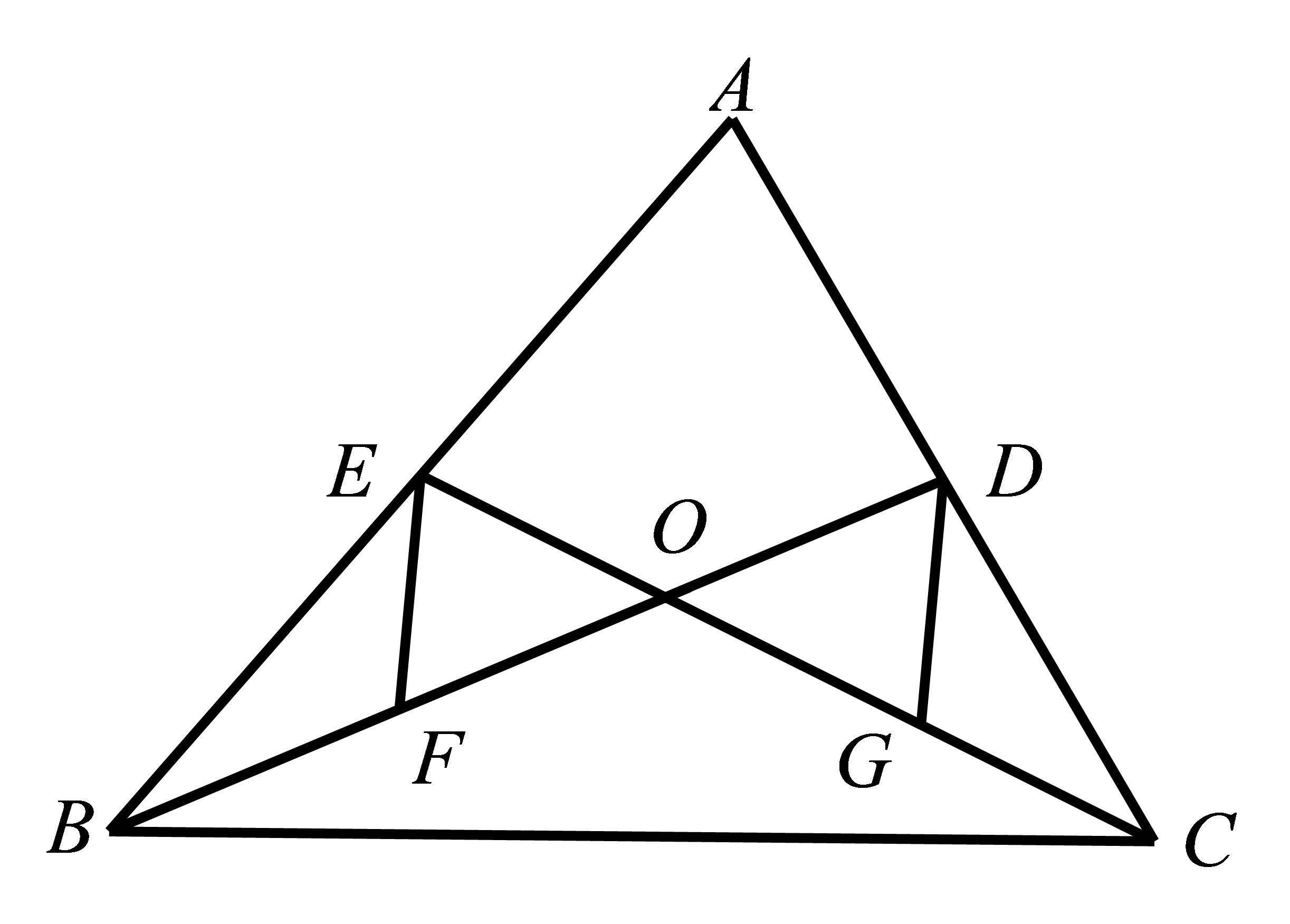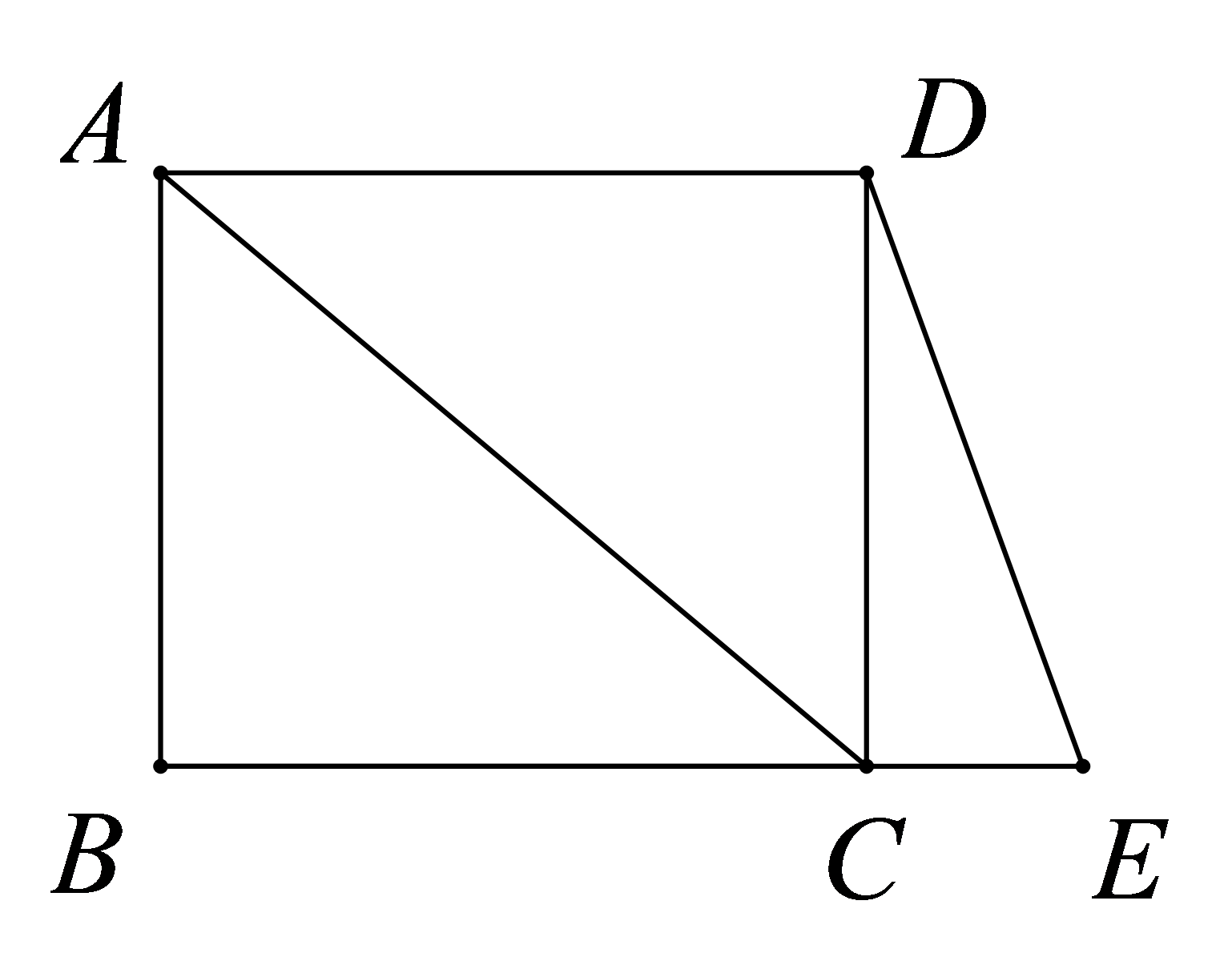“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
第302题 证明:
参考答案:\(FD=EB\)证明:
∵连接\(BD\)交\(AC\)于点\(O\)
∵四边形\(ABCD\)为平行四边形,
\(∴AO=CO,BO=DO\),
\(∵AE=CF,∴EO=FO\),
∴四边形\(DEBF\)为平行四边形。
\(∴DF=EB\)。
\(FB=ED\)证明:
∵连接\(BD\)交\(AC\)于点\(O\)
∵四边形\(ABCD\)为平行四边形,
\(∴AO=CO,BO=DO\)
\(∵AE=CF,∴EO=FO\),
∴四边形\(DEBF\)为平行四边形。
\(∴BF=ED\)。
参考答案:对角线互相平分的四边形是平行四边形
第306题
如图,
参考答案:4;70°
第307题
如图, 
参考答案:4;\(\frac{3}{2}\)
第308题
如图,已知\(DE\)是\(△ABC\)的中位线,\(AF\)是\(BC\)边上的中线. 求证:\(DE\)与\(AF\)互相平分。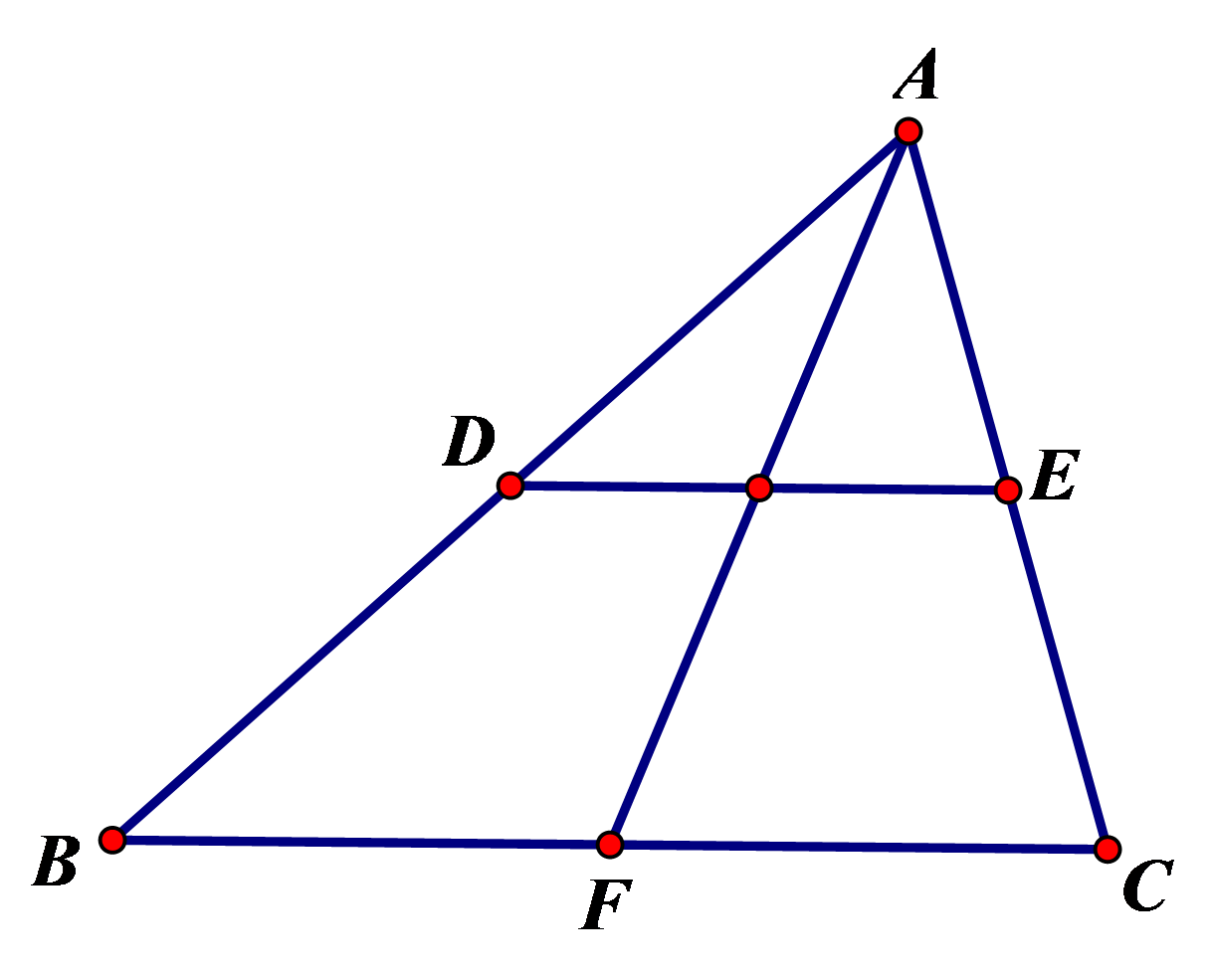
参考答案:证明:连接\(DF,EF\)
\(∵D\)是\(AB\)的中点,
\(F\)是\(BC\)的中点,
\(∴DF\)为\(△BAC\)中位线,
\(∴AC=2DF,AC//DF\)。
∵\(E\)是\(AC\)的中点,
\(∴AC=2AE,\)
\(∴AE=DF,AE//DF\)
∴四边形\(ADFE\)是平行四边形,
\(∴DE\)与\(AF\)互相平分。
参考答案:证明:
\(∵D,E,F,G\)为\(AB,OB,OC,AC\)的中点
\(∴DG\)为\(△ABC\)中位线,
\(∴BC=2DG,BC//DG\),
\(∴EF\)为\(△OBC\)中位线,
\(∴BC=2EF,BC//EF\),
\(∴DG=FE,DG//FE\),
\(∴\)四边形\(DEFG\)是平行四边形。
参考答案:证明:
\(∵CE=DC,AB=DC\),
\(∴CE=AB\)
\(∵AB//DC,\)
\(∴CE//AB\),
\(∴∠BAF=∠E,\)
\(∠ABF=∠FCE\)。
在\(△FAB\)和\(△FEC\)中,
\(∠BAF=∠E,AB\)
\(=CE,∠ABF=∠FCE\)
\(∴△FAB≌△FEC,\)
\(∴BF=CF\),
\(∴F\)为\(BC\)中点,
又\(∵O\)为\(AC\)中点,
\(∴OF\)为\(△CAB\)中位线,
\(∴AB=2OF\)。
第311题
已知:如图,四边形\(ABCD\),点\(E、F、G、H\)分别为边\(AB、BC、CD、DA\)的中点,顺次连结四点得四边形\(EFGH\),求证:四边形\(EFGH\)是平行四边形。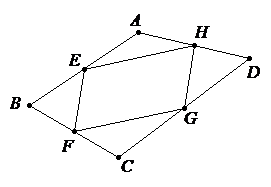
参考答案:证明:连接\(AC\),
∵点\(E、F、G、H\)分别为边\(AB、BC、CD、DA\)的中点
\(∴EF\)为\(△ABC\)中位线,
\(∴AC=2EF,AC//EF\),
\(∴HG\)为\(△DAC\)中位线
\(∴AC=2HG,AC//HG\)
\(∴EF=HG,EF//GH\),
\(∴\)四边形\(EFGH\)是平行四边形。
参考答案:平行且相等。
证明:连接\(AO\) ,
\(∵BD、CE\)为\(△ABC\)的中线,
\(∴D,E\)为边\(AC、AB\)的中点
∵点\(F、G\)分别为\(OB、OC\)的中点,
\(∴EF\)为\(△BAO\)中位线,
\(∴AO=2EF,AO//EF\),
\(∴DG\)为\(△CAO\)中位线,
\(∴AO=2DG,AO//DG,\)
\(∴EF=DG,EF//DG\)。
A.\(40^\circ \)
B.\(45^\circ \)
C.\(50^\circ \)
D.\(60^\circ \)
参考答案:A
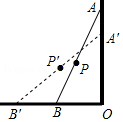
A.下滑时,\(OP\)增大
B.上升时,\(OP\)减小
C.无论怎样滑动,\(OP\)不变
D.只要滑动,\(OP\)就变化
参考答案:C
A.\(\frac{7}{4}\)
B.\(\frac{{25}}{4}\)
C.\(\frac{{25}}{8}\)
D.6
参考答案:B
A.\(2\sqrt 3 \)
B.\(\sqrt 3 \)
C.\(\frac{{\sqrt 3 }}{2}\)
D.2
参考答案:D
第317题
如图,在矩形\(ABCD\)中,\( AB=6\),\( BC=8\),以点\(B\)为圆心,\( BC\)长为半径画弧,交边\(AD\)于点\(E\),则\( DE\)的长为___。
参考答案:\(8 - 2\sqrt 7 \)
参考答案:25;65
参考答案:10;\(5\sqrt 3 \)
参考答案:\(\frac{{13}}{2}\)