初中数学八年级下册（648题）

---

如图，\(E\)为\(▱ABCD\)中\(DC\)边的延长线上的一点，且\(CE=DC\)，连接\(AE\)分别交\(BC\)，\(BD\)于点\(F\)，点\(G\)，连接\(AC\)交\(BD\)于点\(O\)，连接\(OF\)。求证：\(AB=2OF\)。

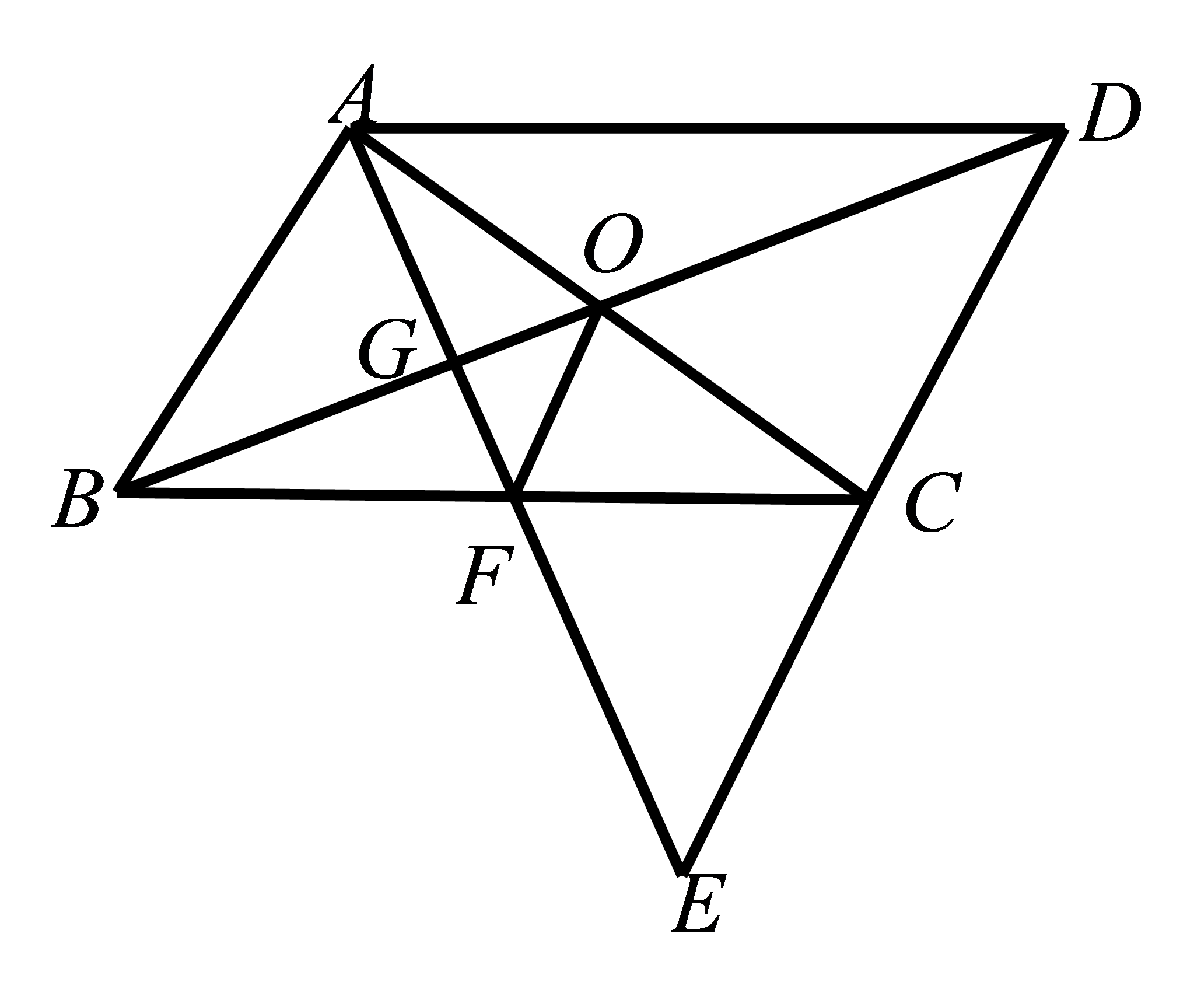
知识点：第十八章　平行四边形

参考答案：证明：
\(∵CE=DC，AB=DC\)，
\(∴CE=AB\)
\(∵AB//DC，\)
\(∴CE//AB\)，
\(∴∠BAF=∠E，\)
\(∠ABF=∠FCE\)。
在\(△FAB\)和\(△FEC\)中，
\(∠BAF=∠E，AB\)
\(=CE，∠ABF=∠FCE\)
\(∴△FAB≌△FEC，\)
\(∴BF=CF\)，
\(∴F\)为\(BC\)中点，
又\(∵O\)为\(AC\)中点，
\(∴OF\)为\(△CAB\)中位线，
\(∴AB=2OF\)。