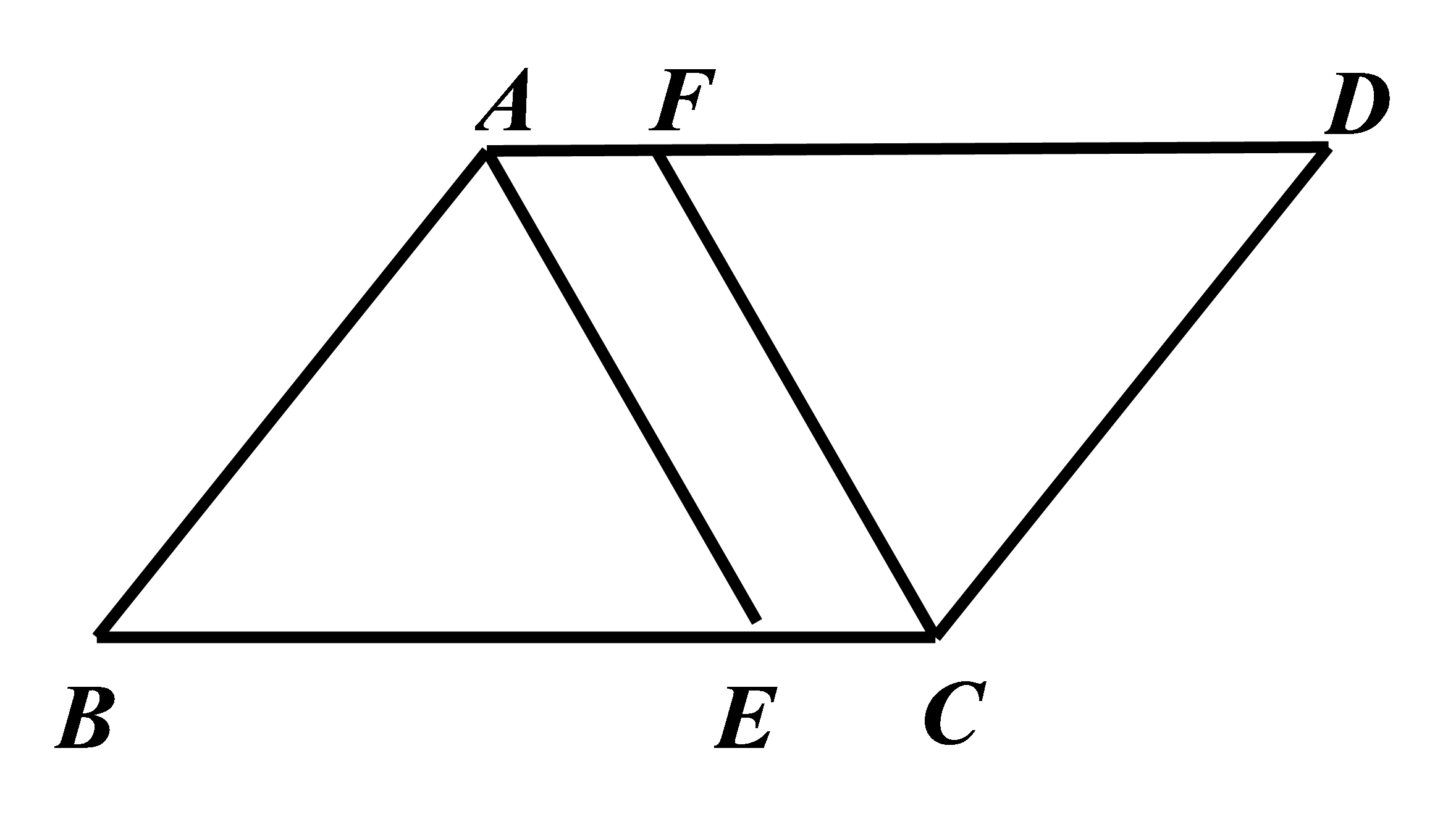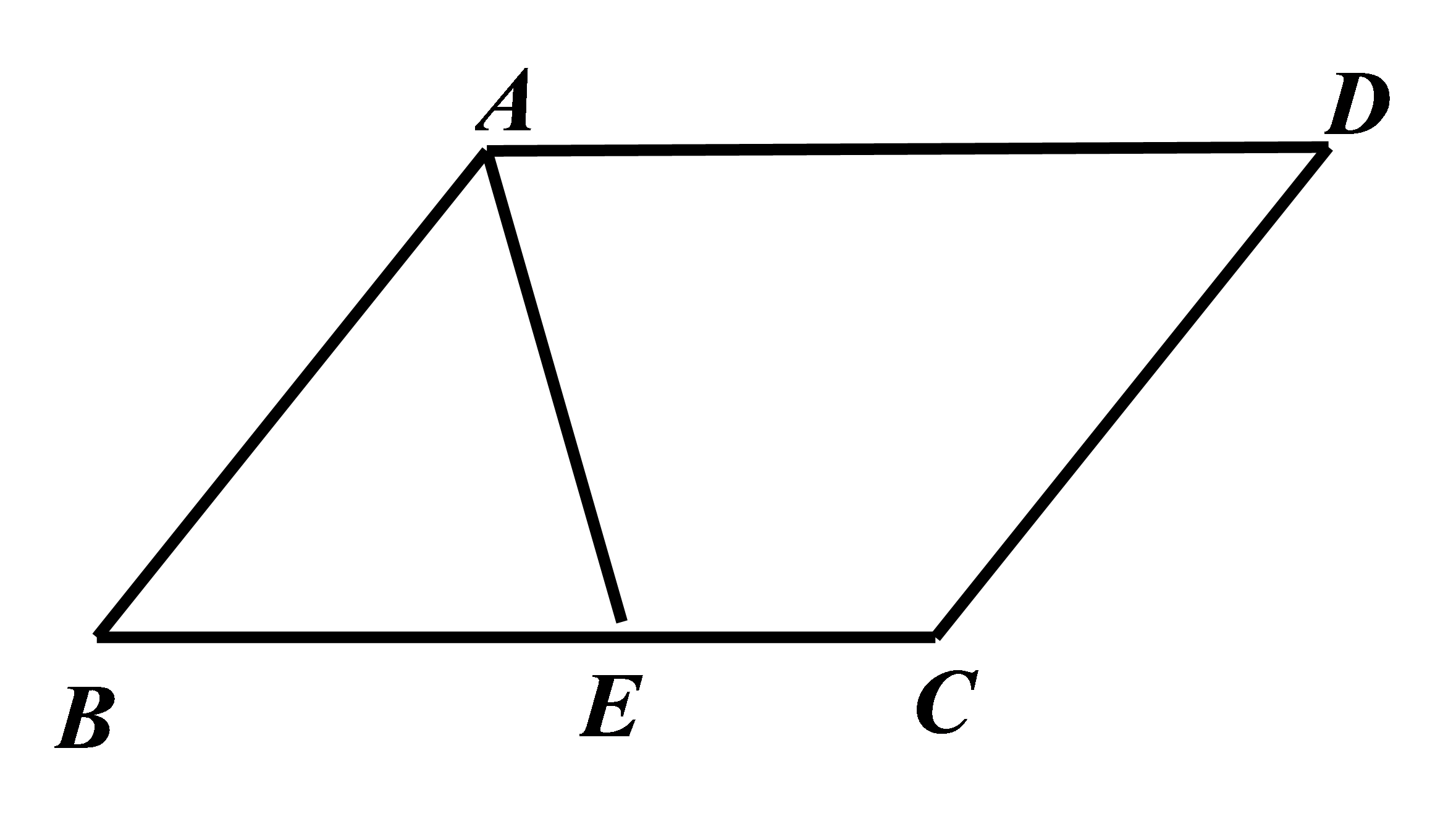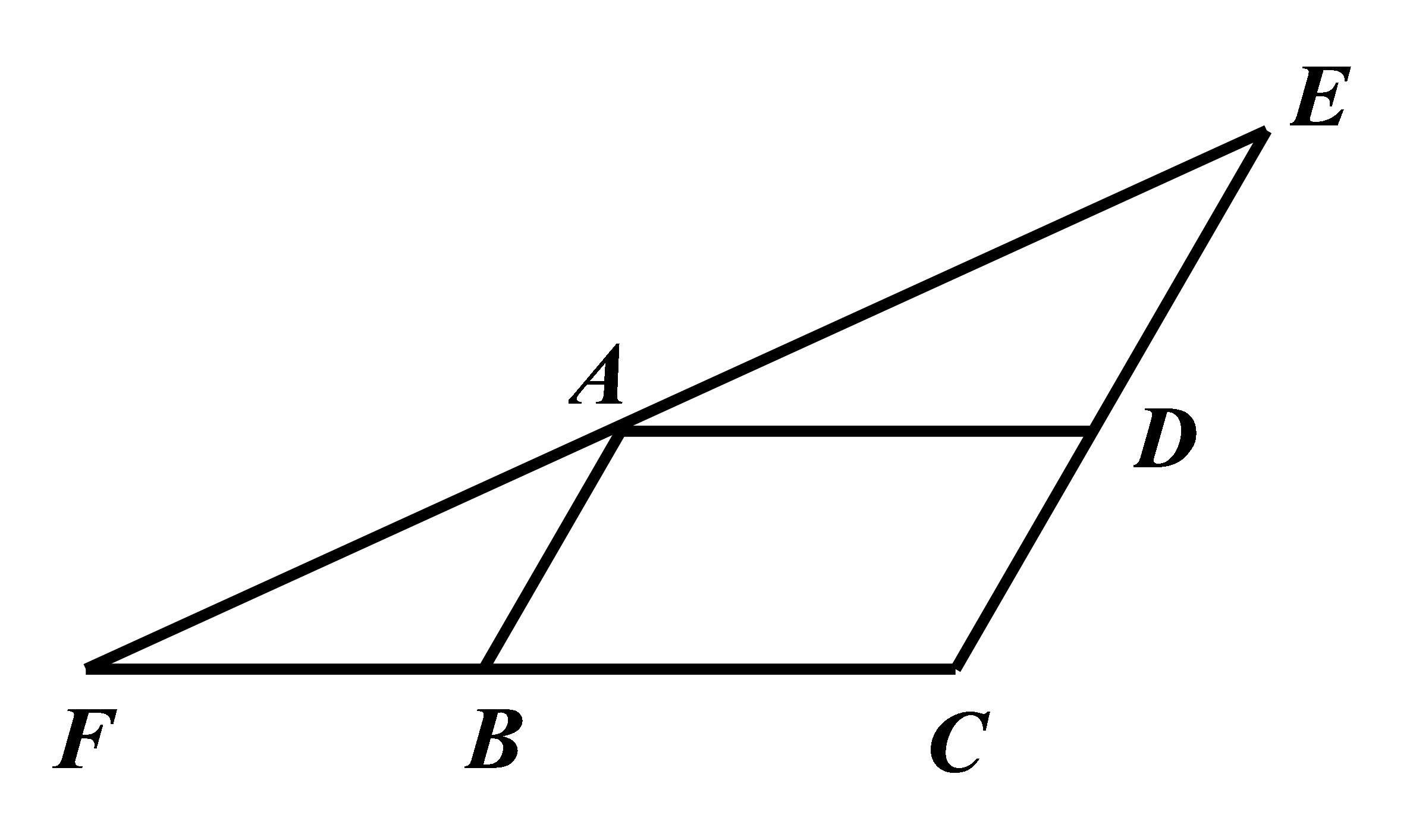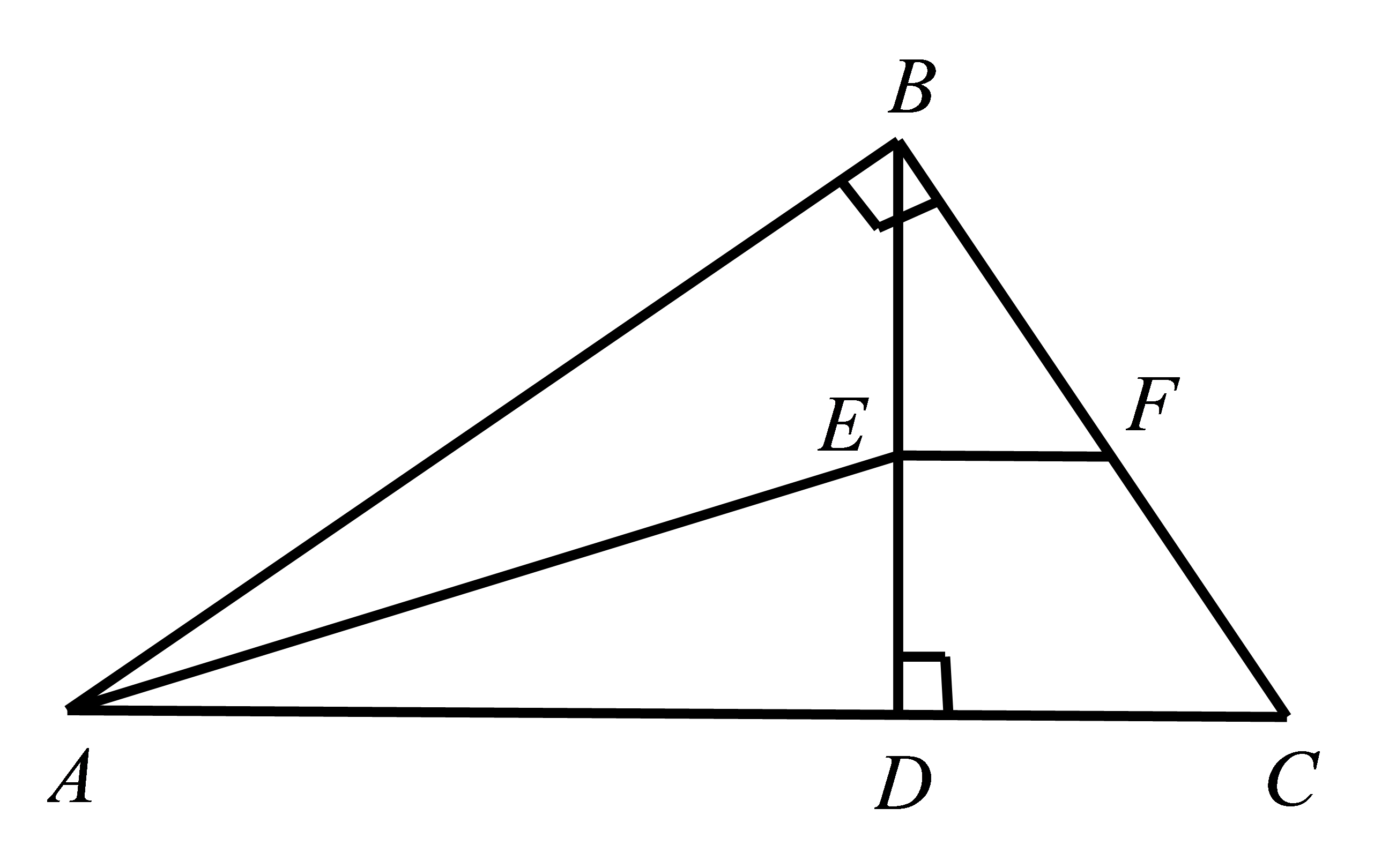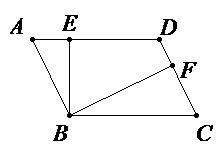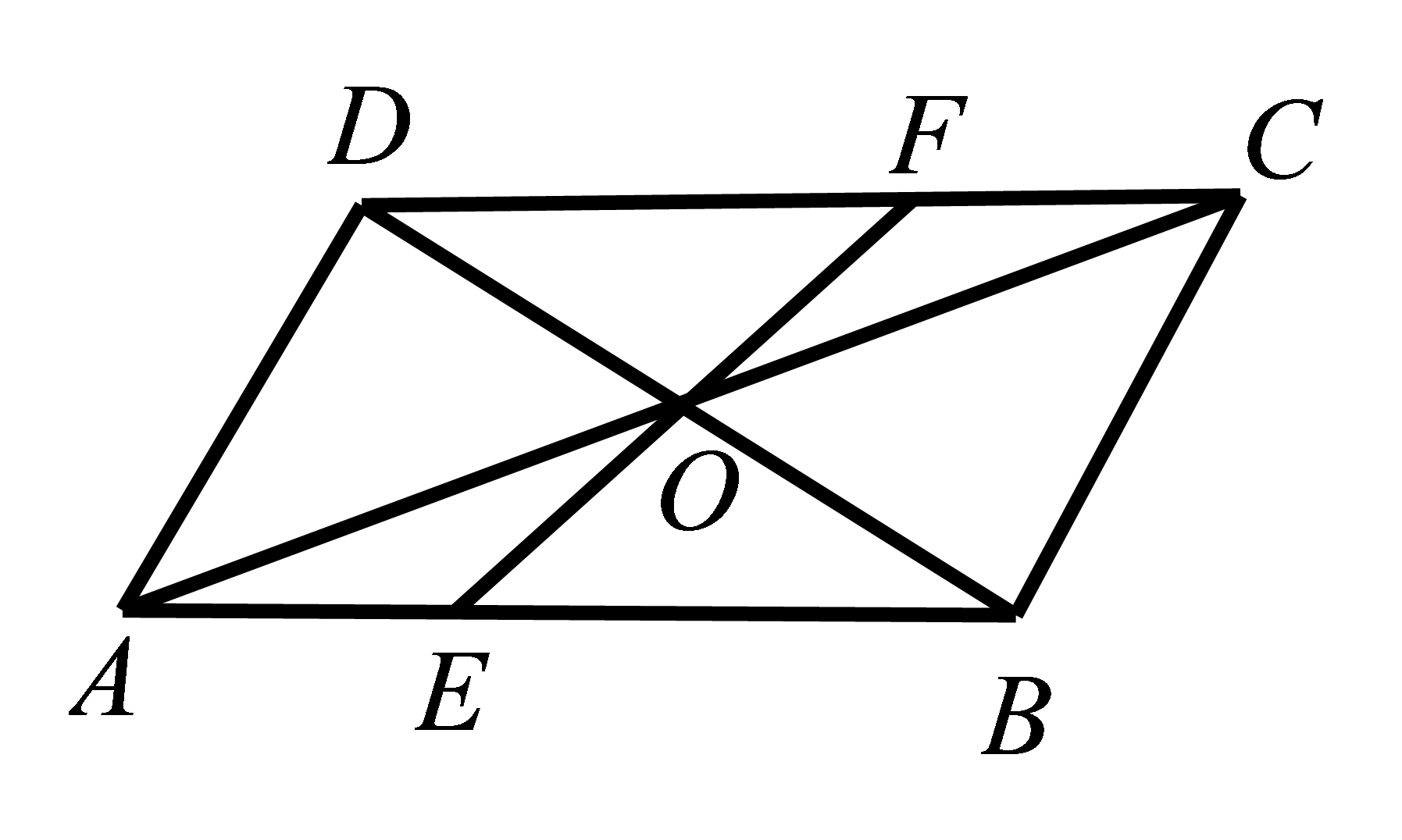“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
参考答案:110°;70°
第264题
参考答案:20;10
参考答案:证明:\(\because ▱ABCD\),\( \therefore \mathrm{\angle }B=\mathrm{\angle }D,AB=CD\)。
在\( △AEB\)和\( △CFD\)中,\( \because \mathrm{\angle }AEB=\mathrm{\angle }CFD\),\( \mathrm{\angle }B=\mathrm{\angle }D\),\( AB=CD\),\( \therefore △AEB≌△CFD(\mathrm{A}\mathrm{A}\mathrm{S})\),\( \therefore AE=CF\)。
第266题
如图,\(▱ABCD\),\( BQ,DP\)相交于\( C\),\( △BCP\)和\( △CDQ\)均为等边三角形。求证:\( △APQ\)是等边三角形。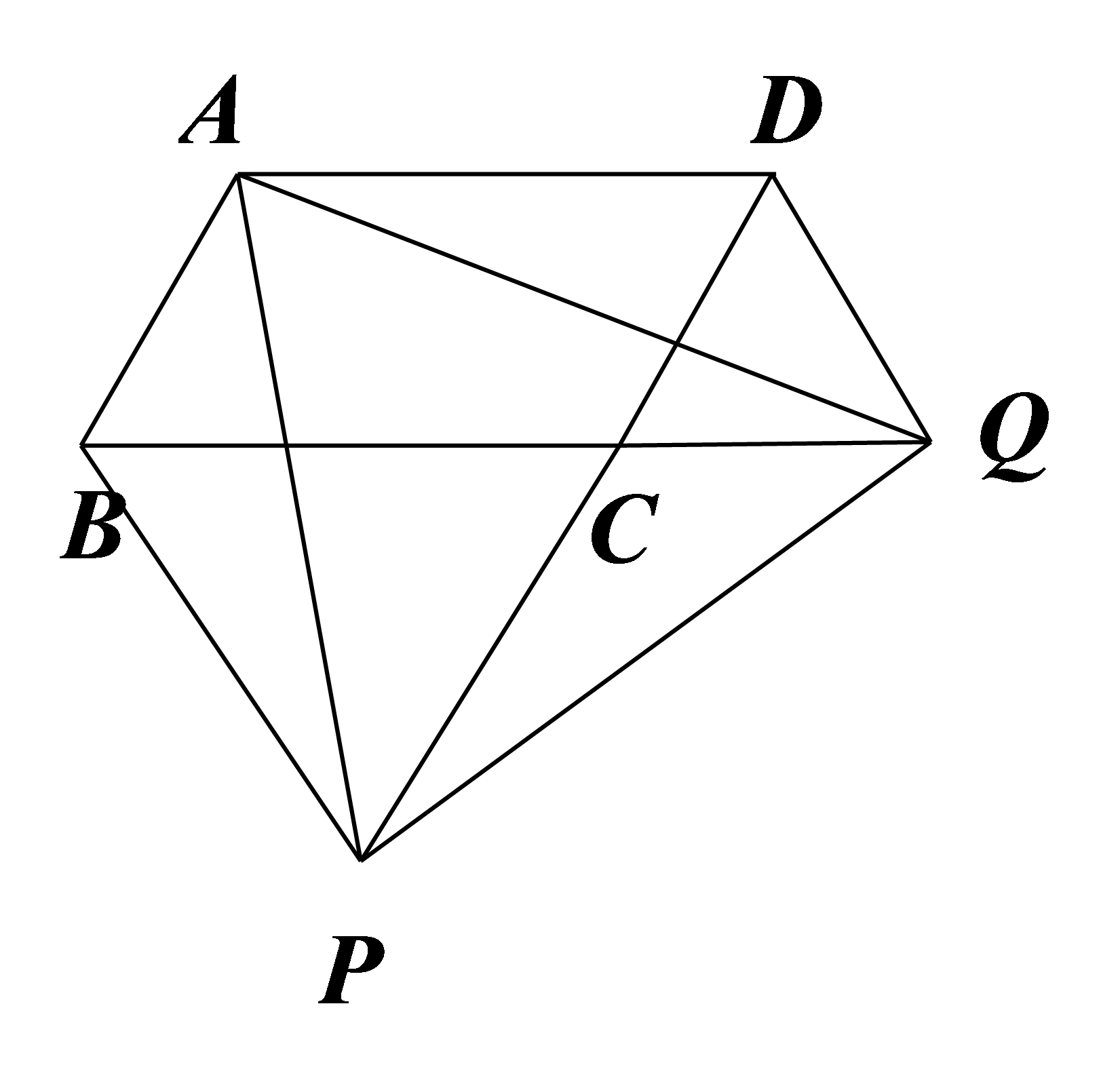
参考答案:证明:\( \because △BCP\)和\( △CDQ\)是等边三角形,
\( \therefore \mathrm{\angle }PBC=\mathrm{\angle }PCB=60°\),\( PC=PB,CQ=CD\)。
\(\because ▱ABCD\),
\(\therefore AB=CD=CQ,AB//CD\),
\(\therefore \mathrm{\angle }ABC=\mathrm{\angle }BCP=60°\),
\(\therefore \mathrm{\angle }PCQ=180°-\mathrm{\angle }BCP=120°\),
\(\mathrm{\angle }ABP=\mathrm{\angle }ABC+\mathrm{\angle }CBP=120°\)。
在\( △BAP\)和\( △CQP\)中,\( \because BA=CQ\),
\(\mathrm{\angle }ABP=\mathrm{\angle }QCP,BP=CP\),
\(\therefore △BAP≌△CQP(\mathrm{S}\mathrm{A}\mathrm{S})\),
\( \therefore PA=PQ,\mathrm{\angle }APB=\mathrm{\angle }QPC\)。
\( \therefore \mathrm{\angle }APQ=\mathrm{\angle }QPC+\mathrm{\angle }APD\)
\(=\mathrm{\angle }APB+\mathrm{\angle }APD=60°\),
\(\therefore △APQ\)是等边三角形。
参考答案:2
第268题
如图,在\(▱ABCD\)中,\( BC=2CD\),\( E\)为\( AD\)的中点,\( CE,BA\)的延长线交于点\( F\),连接\( BE\). 求证:\( BE\perp CF\)。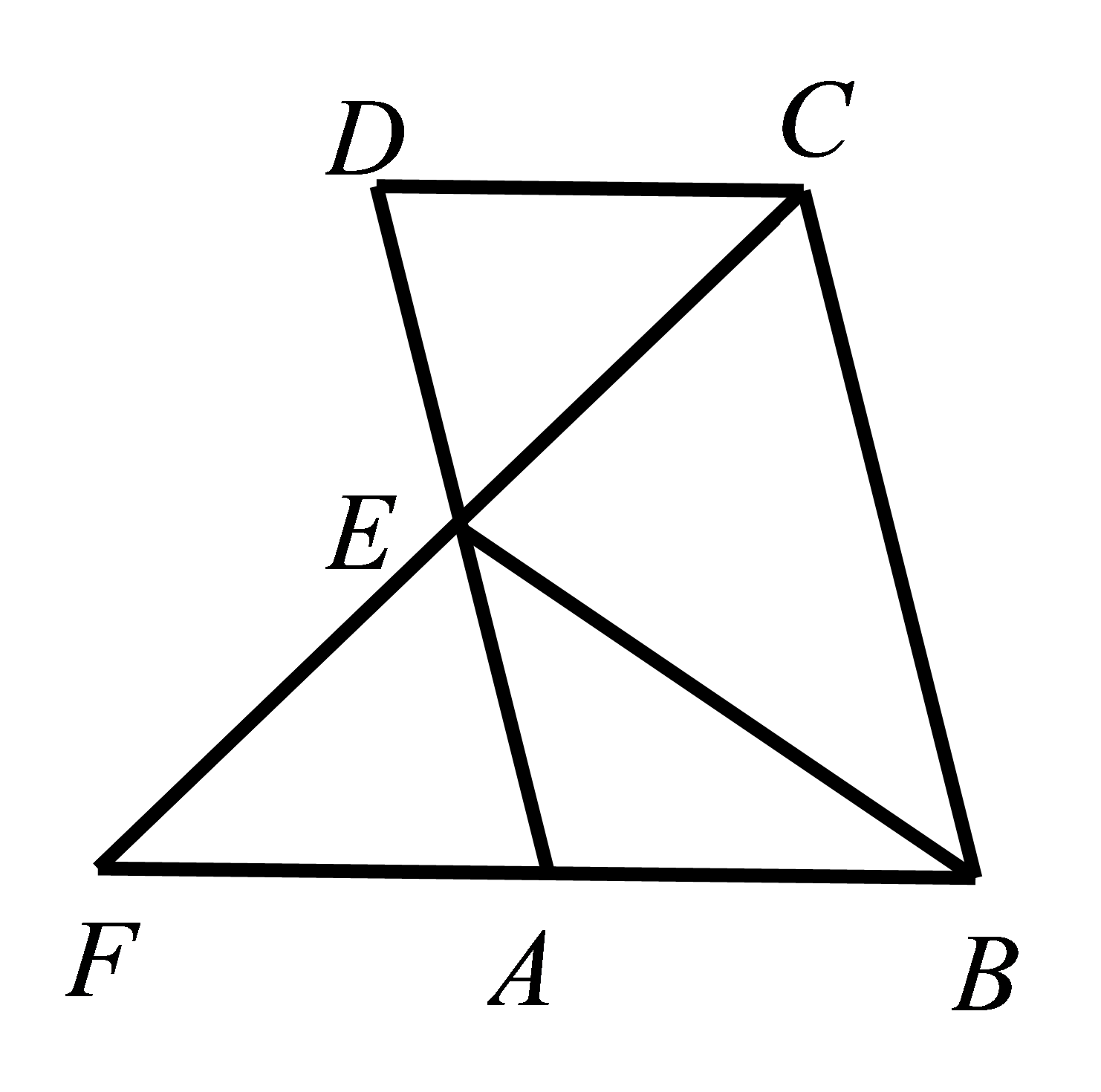
参考答案:证明:
\(\because ▱ABCD,\)
\(\therefore AB//CD,\)
\(\therefore \mathrm{\angle }D=\mathrm{\angle }DAF,\mathrm{\angle }F=\mathrm{\angle }DCF\),
\( \because E\)为\( AD\)的中点,
\( \therefore DE=AE\)。
在\( △CDE\)和\( △FAE\)中,
\( \because \mathrm{\angle }D=\mathrm{\angle }DAF\),
\( \mathrm{\angle }F=\mathrm{\angle }DCF\),\( DE=AE\),
\( \therefore △CDE≌△FAE\mathrm{ }\left(\mathrm{A}\mathrm{A}\mathrm{S}\right)\),
\( \therefore AF=CD,CE=EF\)。
\( \because BC=2CD,\therefore BC=2AF\)。
\(\because ▱ABCD,\)
\(\therefore AB=CD,\)
\(\therefore AB=AF,\)
\(\because AB+AF=BF,\)
\(\therefore BF=2AF,\)
\(\therefore BC=BF\),
又\( CE=EF\),
\( \therefore E\)为\( CF\)中点,
\( \therefore BE\perp CF\)。
参考答案:判断:\( △CEF\)是等腰三角形。
理由:
\(\because ▱ABCD,\)
\(\therefore AD//BC,\mathrm{}AB//DC,\)
\(\therefore \mathrm{\angle }EAD=\mathrm{\angle }F,\mathrm{\angle }BAF=\mathrm{\angle }E\)
\( \because \mathrm{\angle }EAD=\mathrm{\angle }BAF,\)
\(\therefore \mathrm{\angle }F\mathrm{ }=\mathrm{\angle }E,\)
\(\therefore △CEF\)是等腰三角形。
参考答案:
证明:如图,在

在
参考答案:
证明:如图,在
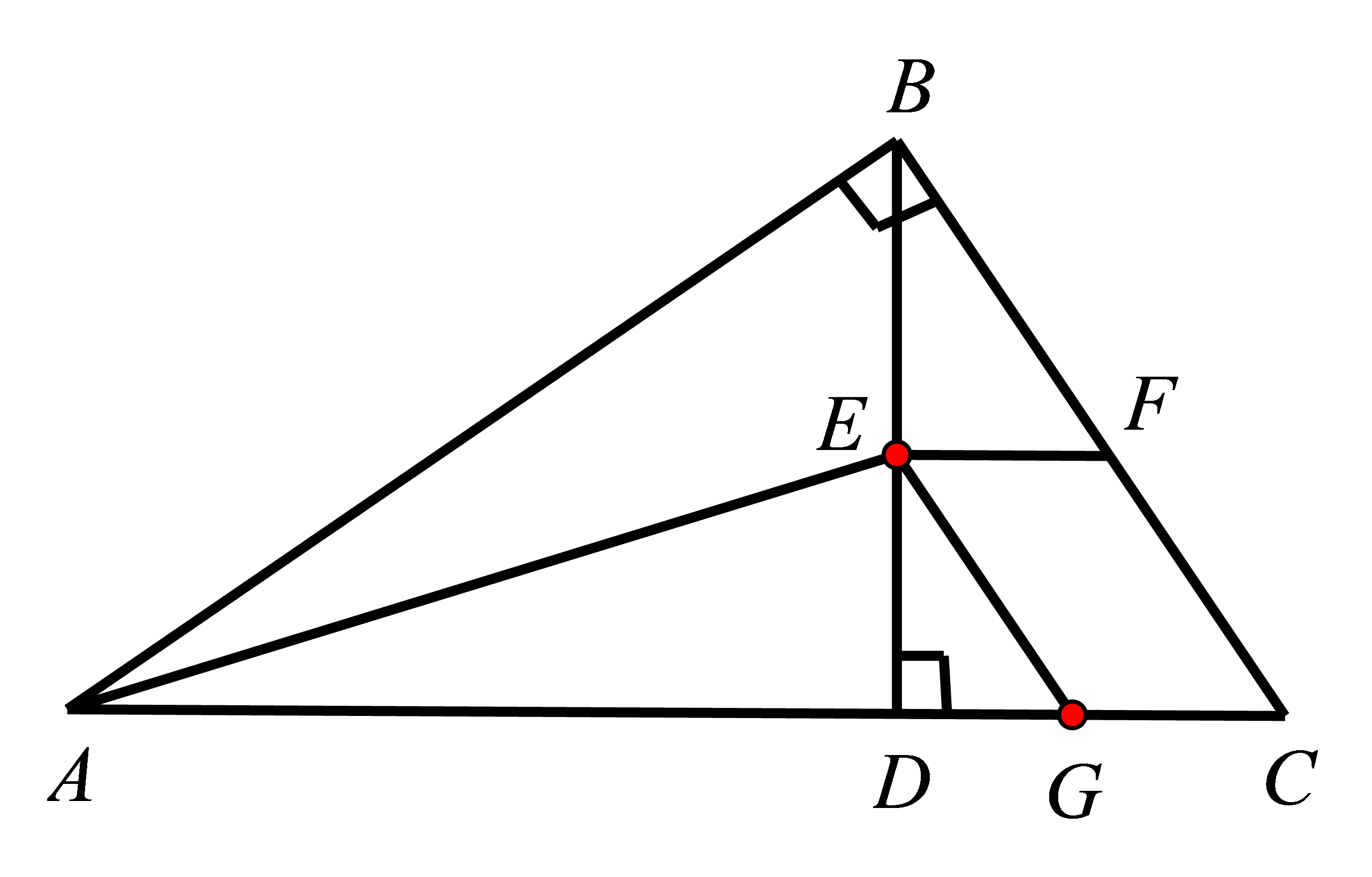
在
又
参考答案:10+2\(\sqrt {13} \)
第273题
已知在平面直角坐标系中,
参考答案:\( {D}_{1}(2,5)\),\( {D}_{2}(-6,-1)\),\( \mathrm{ }{D}_{3}(8,-3)\)
参考答案:\(\frac{{36}}{5}\)
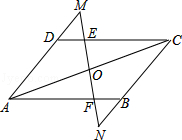
参考答案:证明:\(\because ▱ABCD\mathrm{}\),\( AC\)与\( BD\)交于\( O\),\( \therefore OA=OC,\mathrm{ }CD//AB\),\( \therefore \mathrm{\angle }DCA=\mathrm{\angle }CAB\)。
在\( △OEA\)和\( △OFC\)中,\( \because \mathrm{\angle }CAB=\mathrm{\angle }DCA,OA=OC,\mathrm{\angle }AOE=\mathrm{\angle }COF\),\( \therefore △OEA≌△OFC(\mathrm{A}\mathrm{S}\mathrm{A}),\therefore OE=OF\)。
参考答案:证明:
\(\because ▱ABCD\mathrm{},\)
\(\therefore AD=BC,\mathrm{}AD//BC,\)
\(\therefore \mathrm{\angle }DAC=\mathrm{\angle }ACB\)。
在\( △OAM\)和\( △OCN\)中,
\( \because \mathrm{\angle }DAC=\mathrm{\angle }ACB,OA=OC,\mathrm{\angle }AOE=\mathrm{\angle }COF,\)
\(\therefore △OAM≌△OCN(\mathrm{A}\mathrm{S}\mathrm{A}),\)
\(\therefore AM=CN\)
\( \because AD=BC,\therefore DM=BN\)。