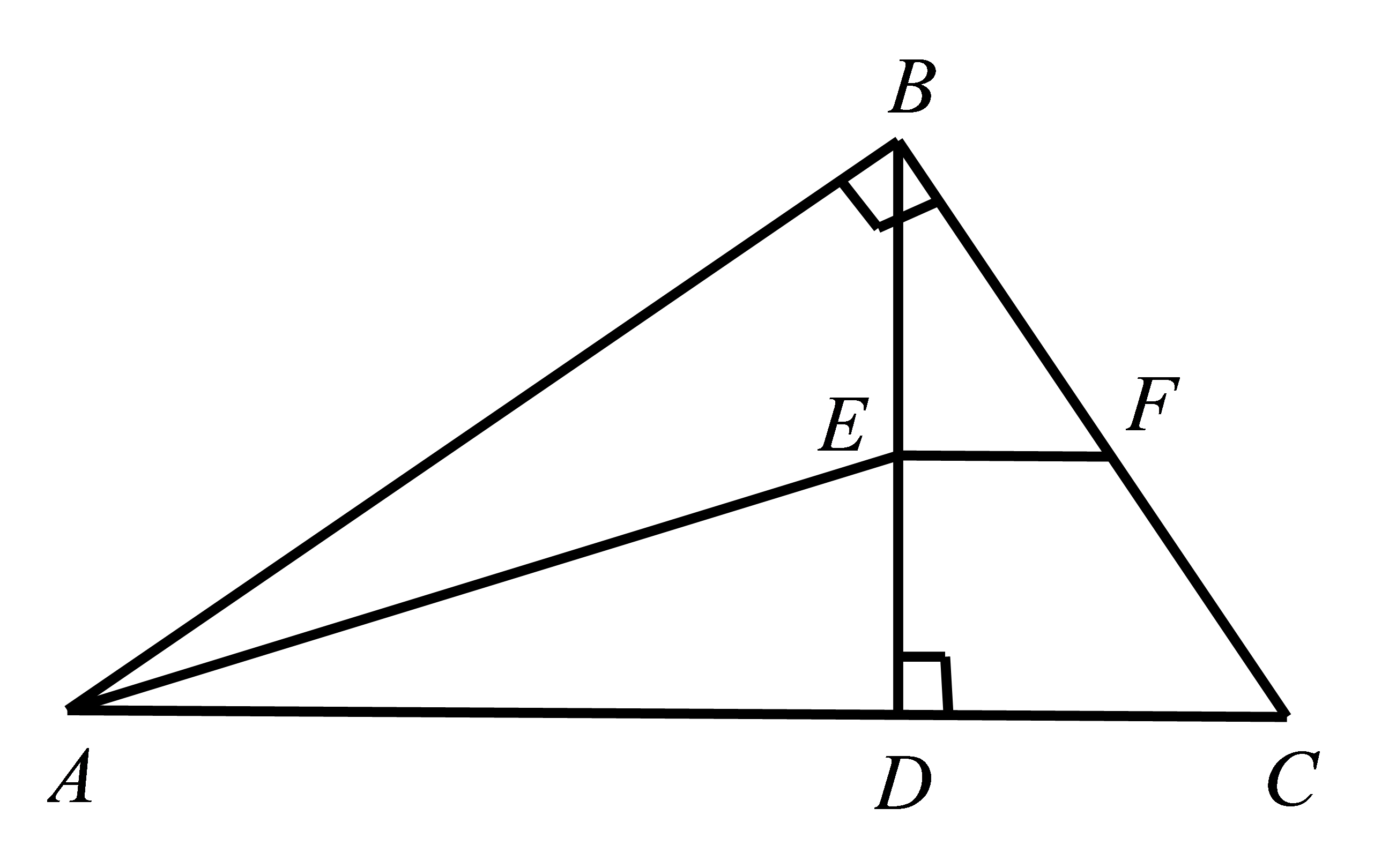如图,在\( △ABC\)中,\( \mathrm{\angle }ABC=90°\),\( BD\perp AC\)于点\( D\), \( AE\)平分\( \mathrm{\angle }BAC\)交\( BD\)于点\( E\),\( EF//DC\),交\( BC\)于点\( F\),求证:\( BE=CF\)。
证明:如图,在\( AC\)上取一点\( G\),使\( AG=AB\),连接\( EG\)。
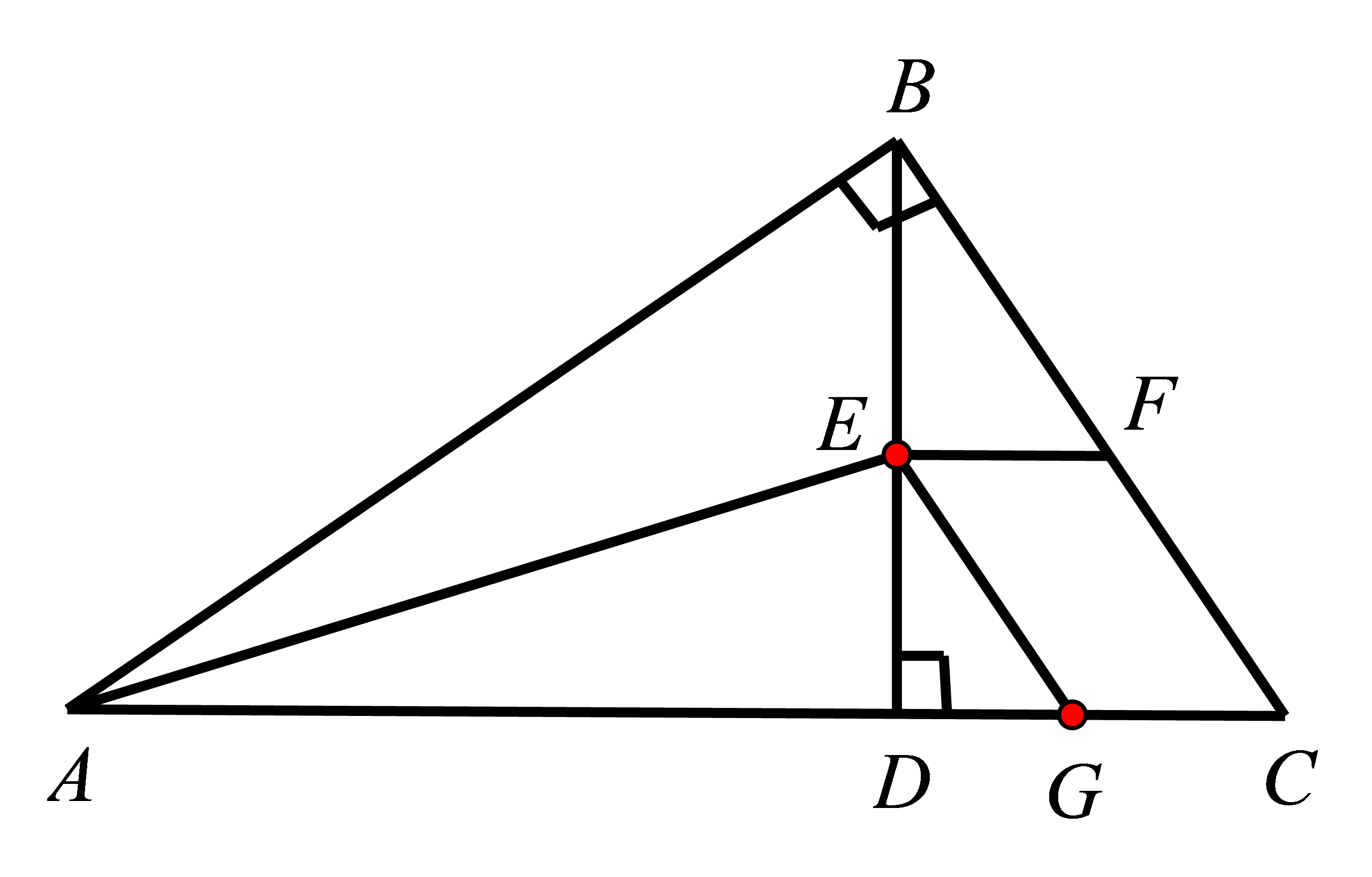
\( \because AE\)平分\( \mathrm{\angle }BAC\)交\( BD\)于点\( E\),\( \therefore \mathrm{\angle }GAE=\mathrm{\angle }BAE\)。
在\( △AHE\)和\( △ABE\)中,\( AB\mathrm{ }=AG\),\( \mathrm{\angle }GAE=\mathrm{\angle }BAE\),\( AE=AE\),\( \therefore △AGE≌△ABE(\mathrm{S}\mathrm{A}\mathrm{S})\)
\( \therefore EG=BE,\mathrm{ }\mathrm{\angle }ABE=\mathrm{\angle }AGE\)。
\( \because \mathrm{\angle }ABC=90°\),\( BD\perp AC\)于点\( D\),\( \therefore \mathrm{\angle }ABD\mathrm{ }+\mathrm{\angle }CBD\mathrm{ }=90°\),\( \mathrm{\angle }C+\mathrm{\angle }CBD\mathrm{ }=90°\)
\( \therefore \mathrm{\angle }ABD\mathrm{ }=\mathrm{\angle }C,\)\(\therefore \mathrm{\angle }AGE\mathrm{ }=\mathrm{\angle }C,\)\(\therefore \mathrm{ }EG//FC\)。
又\( \because EF//DC\),∴四边形\( EHCF\)为平行四边形,\( \therefore \mathrm{ }EG=CF,\therefore BE=CF\)。