初中数学八年级下册（648题）

---

如图，\(▱ABCD\)，\( BQ，DP\)相交于\( C\)，\( △BCP\)和\( △CDQ\)均为等边三角形。求证：\( △APQ\)是等边三角形。

    

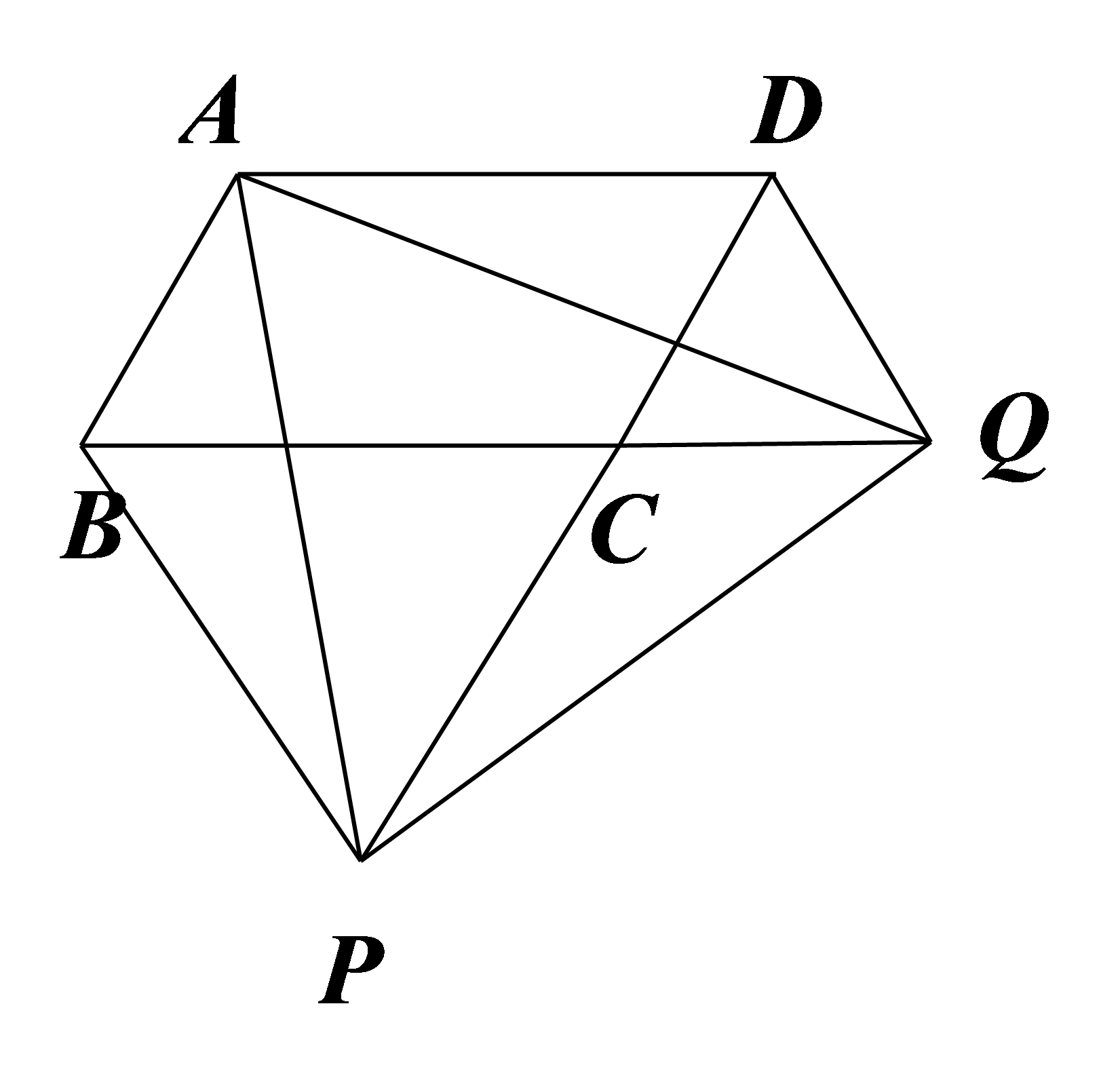
知识点：第十八章　平行四边形

参考答案：证明：\( \because △BCP\)和\( △CDQ\)是等边三角形，
\( \therefore \mathrm{\angle }PBC=\mathrm{\angle }PCB=60°\)，\( PC=PB，CQ=CD\)。

\(\because ▱ABCD\)，
\(\therefore AB=CD=CQ，AB//CD\)，

\(\therefore \mathrm{\angle }ABC=\mathrm{\angle }BCP=60°\)，

\(\therefore \mathrm{\angle }PCQ=180°-\mathrm{\angle }BCP=120°\)，

\(\mathrm{\angle }ABP=\mathrm{\angle }ABC+\mathrm{\angle }CBP=120°\)。

在\( △BAP\)和\( △CQP\)中，\( \because BA=CQ\)，

\(\mathrm{\angle }ABP=\mathrm{\angle }QCP，BP=CP\)，

\(\therefore △BAP≌△CQP（\mathrm{S}\mathrm{A}\mathrm{S}）\)，


\( \therefore PA=PQ，\mathrm{\angle }APB=\mathrm{\angle }QPC\)。

\( \therefore \mathrm{\angle }APQ=\mathrm{\angle }QPC+\mathrm{\angle }APD\)
\(=\mathrm{\angle }APB+\mathrm{\angle }APD=60°\)，

\(\therefore △APQ\)是等边三角形。