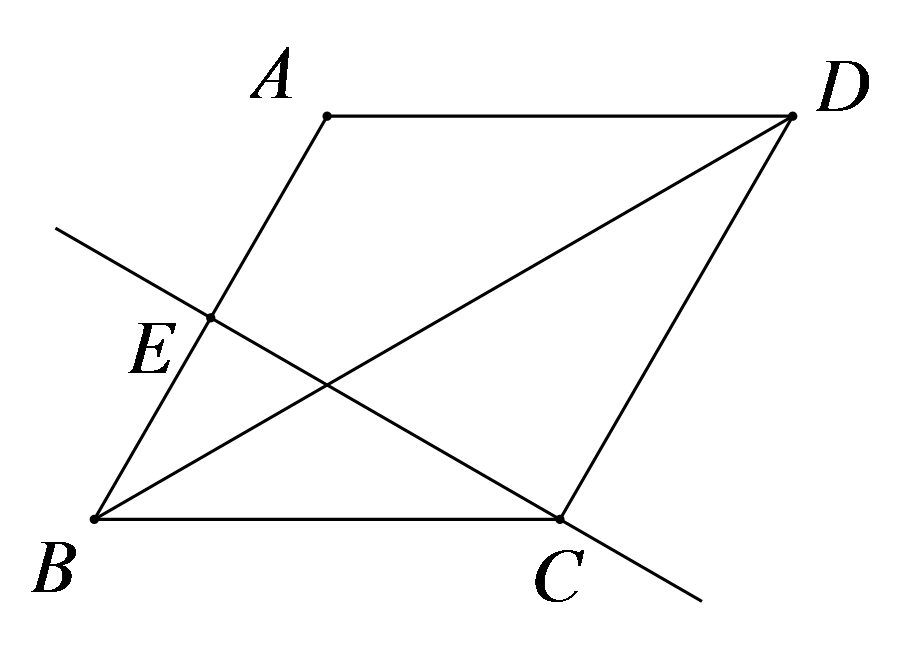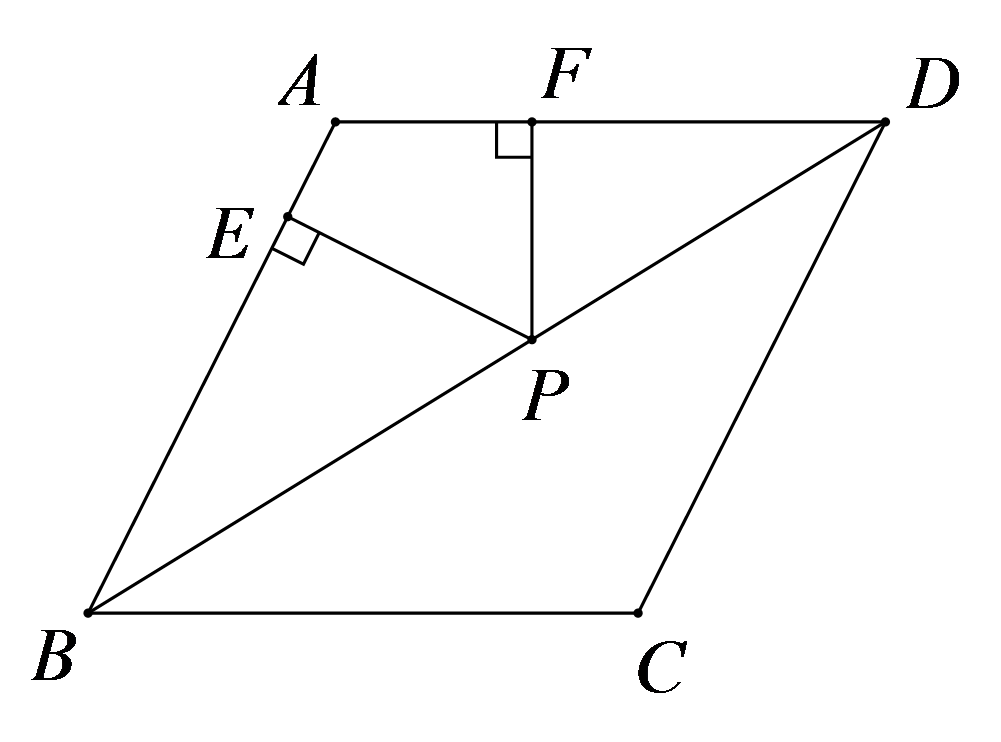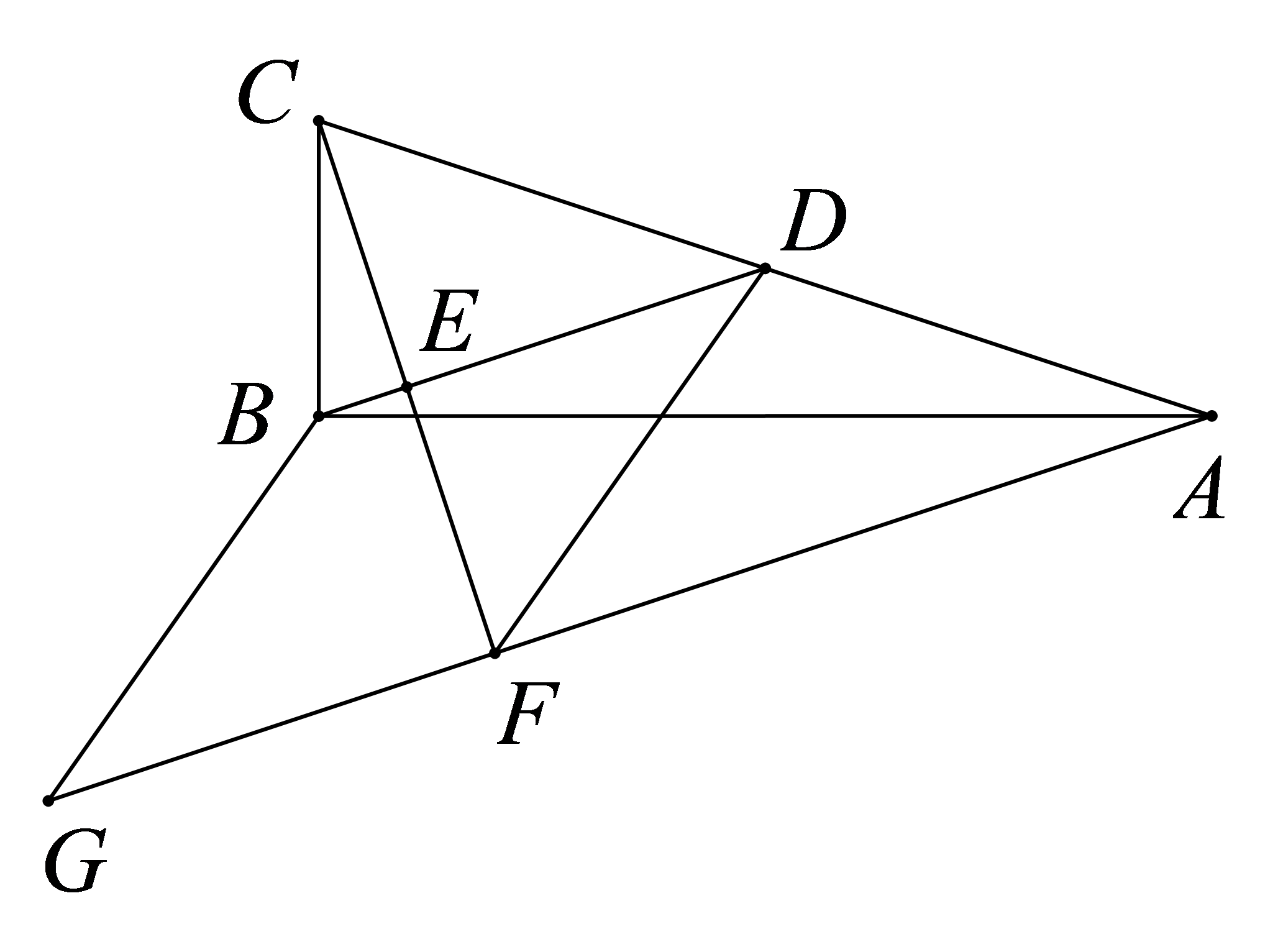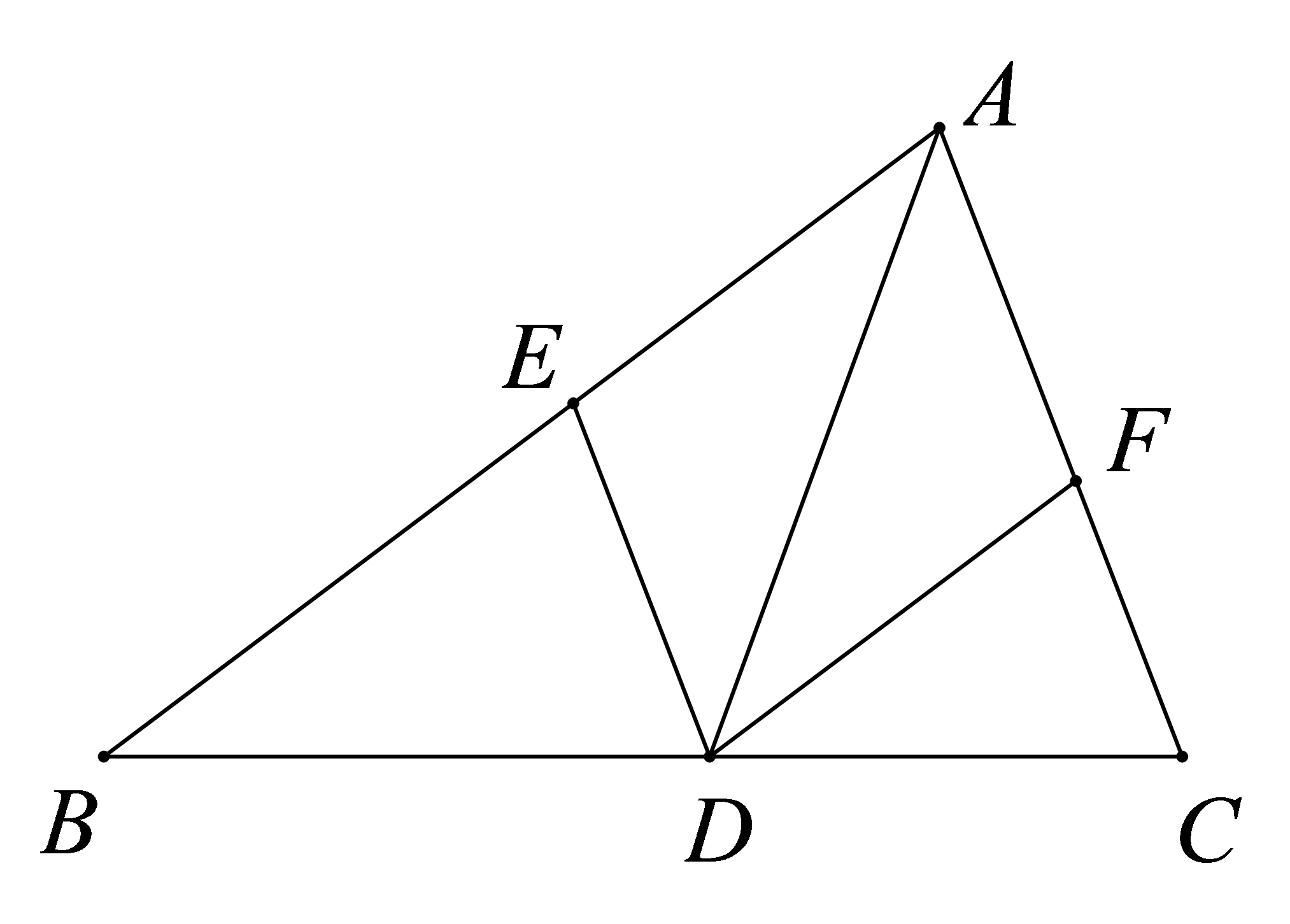第341题

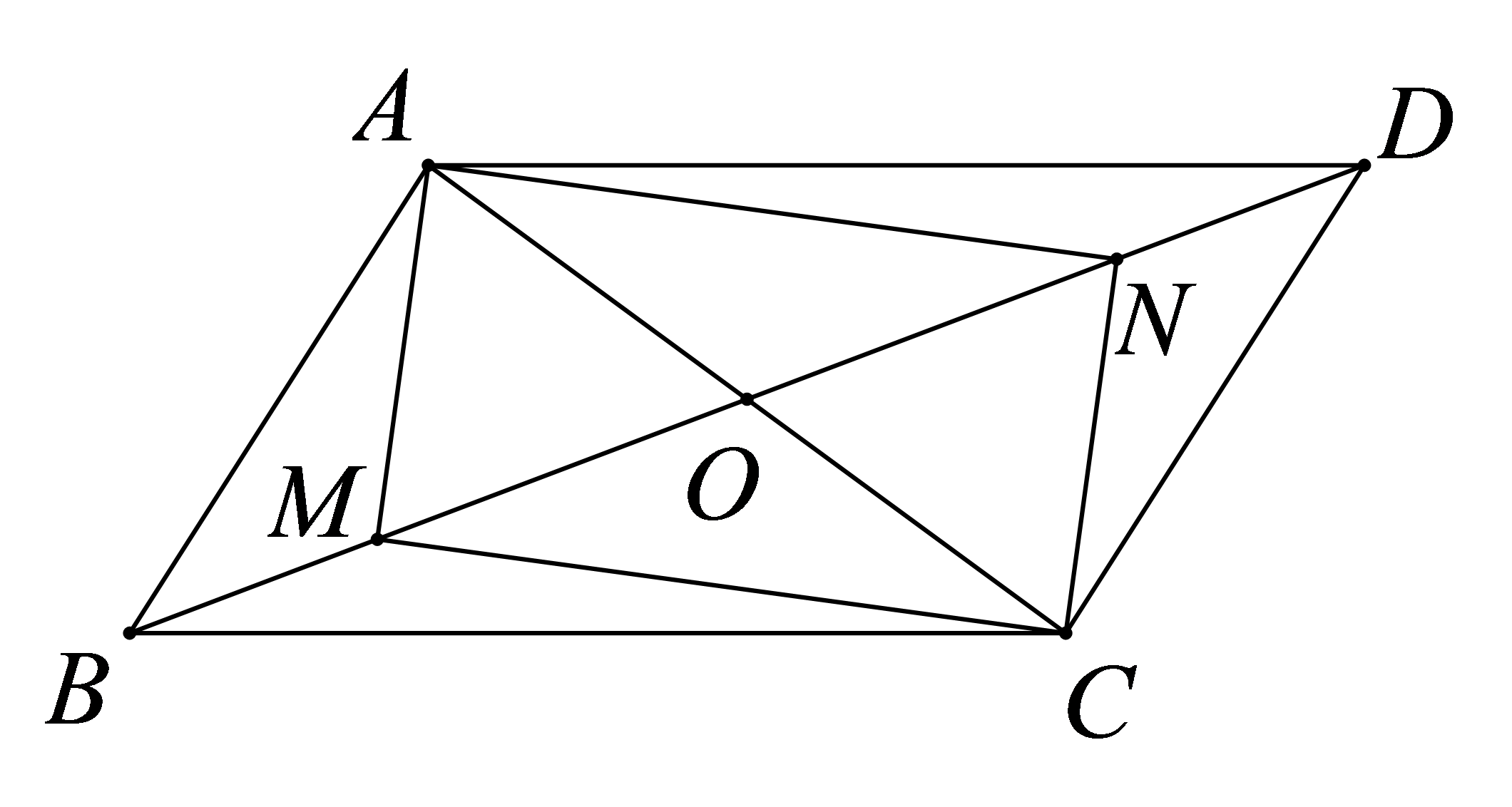
参考答案：证明：
\(\because \)四边形\(ABCD\)是平行四边形，
\(\therefore OA = OC\)，\(OB = OD\)，
\(\because BM = DN\)，
\(\therefore OB - BM = OD - DN\)，即\(OM = ON\)，
\(\therefore \)四边形\(AMCN\)是平行四边形，
\(\because MO = NO\)，
\(\therefore MN = 2MO\)，
\(\because AC = 2MO\)，
\(\therefore MN = AC\)，
\(\therefore \)四边形\(AMCN\)是矩形。

第342题 菱形的一个内角是\(60^\circ \)，周长是\(12\text{cm}\)，则这个菱形的较短的对角线长是（    ）

A.\(\frac {3} {2}\text{cm}\)

B.\(\frac {3} {2}\sqrt {3}\text{cm}\)

C.\(3\text{cm}\)

D.\(3\sqrt {3}\text{cm}\)

参考答案：C

第343题

A.对角线互相平分

B.邻角互补

C.对角相等

D.每条对角线平分一组对角

参考答案：D

第344题

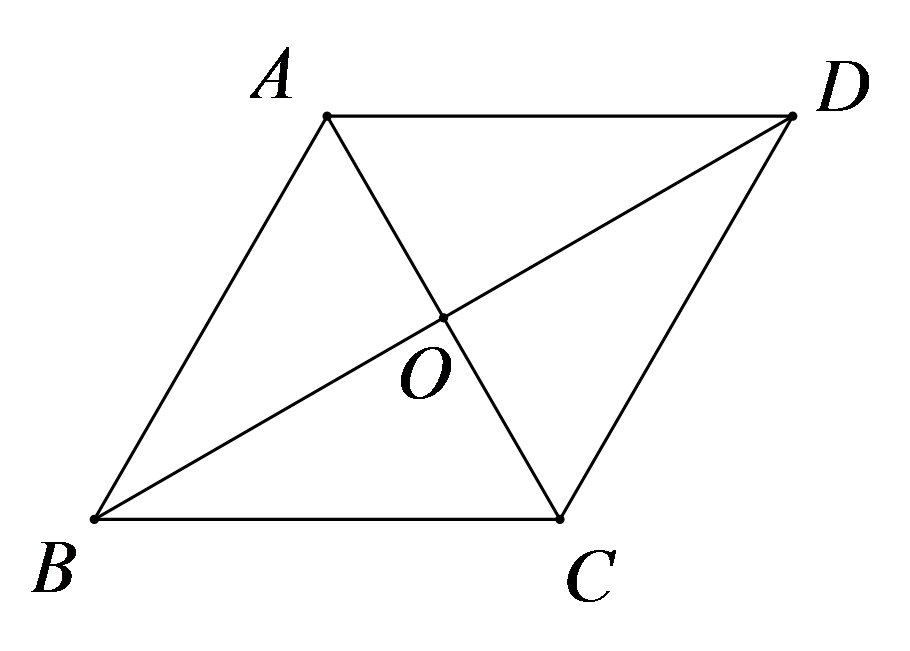
A.36

B.24

C.12

D.6

参考答案：B

第345题

参考答案：4

第346题

如图，四边形\(ABCD\)是菱形，\(AC=8\text{cm}\)，\(DB=6\text{cm}\)，\(DH \bot AB\)于\(H\)，则\(DH\)等于（   ）。

A.3.6

B.4.8

C.5

D.10

参考答案：B

第347题

参考答案：140°

第348题

参考答案：30°

第349题

参考答案：24

第350题

参考答案：12

第351题

参考答案：8

第352题

参考答案：证明：\(\because \)四边形\(ABCD\)是菱形，\(\therefore AB = AD = BC = CD\)，\(\angle B = \angle D\)，在\(\Delta ABE\)和\(\Delta ADF\)中，\(\left\{ {\begin{array}{*{20}{l}}
{\angle BAE = \angle DAF} \\
{AB = AD} \\
{\angle B = \angle D}
\end{array}} \right.\)，\(\therefore \Delta ABE \cong \Delta ADF(ASA)\)，\(\therefore BE = DF\)，\(\therefore BC - BE = CD - DF\)，即\(CE = CF\)。

第353题

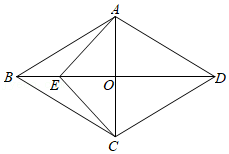
如图，菱形\(ABCD\)中，对角线\(AC，BD\)相交于点\(O，E\)为\(AB\)的中点．若菱形\(ABCD\)的周长为48，则\(OE\)的长为（　　）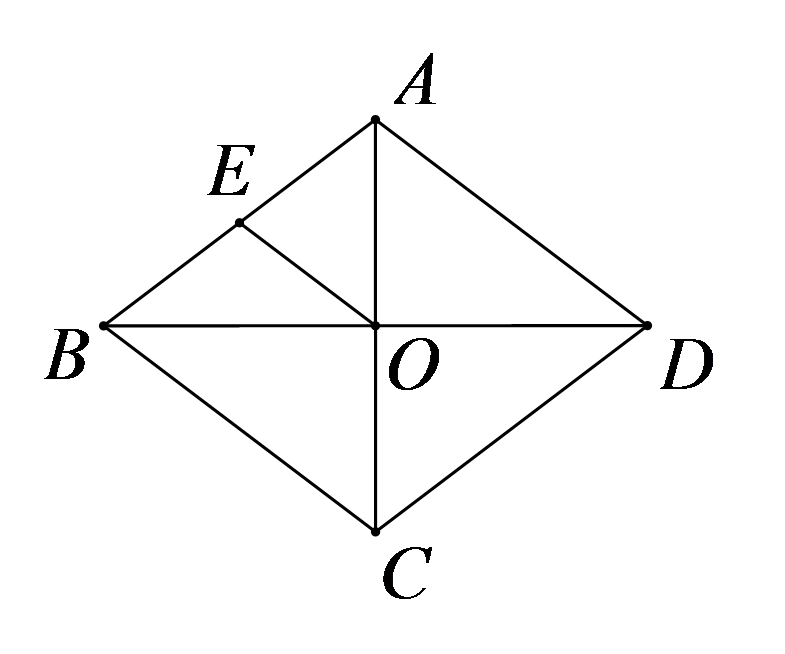

A.4

B.5

C.6

D.8

参考答案：C

第354题

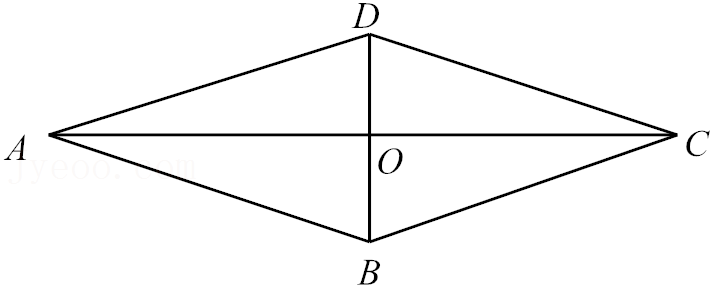
参考答案：解：
\(\because \)四边形\(ABCD\)是菱形，\(BD = 10\)，\(AC = 24\)，
\(\therefore AB = BC = CD = AD\)，\(OA = \frac{1}{2}AC = 12\)，\(OB = \frac{1}{2}BD = 5\)，\(AC \bot BD\)，
\(\therefore \angle AOB = 90^\circ \)，
\(\therefore AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{{12}^2} + {5^2}} = 13\)，
\(\therefore \)菱形的周长\( = 4AB = 52\)．

第355题

如图，菱形\(ABCD\)的对角线\(AC\)与\(BD\)相交于点\(O\)，点\(E\)在\(BD\)上，连接\(AE\)，\(CE\)，\(\angle ABC = 60^\circ \)，\(\angle BCE = 15^\circ \)，\(ED = 4 + 4\sqrt 3 \)，求\(AD\)的长。

参考答案：解：
\(\because \)四边形\(ABCD\)是菱形，\(\angle ABC = 60^\circ \)，
\(\therefore \angle ADC = 60^\circ \)，\(\angle BCD = 120^\circ \)，\(AC \bot BD\)，\(AO = CO\)，\(\angle ADB = \angle CDB = 30^\circ \)，\(\angle ACD = \angle ACB = 60^\circ \)，
\(\therefore DO = \sqrt 3 CO = \sqrt 3 AO\)，\(AD = 2AO\)，
\(\because \angle BCE = 15^\circ \)，
\(\therefore \angle ACE = 45^\circ \)，
\(\therefore \angle ACE = \angle DEC = 45^\circ \)，
\(\therefore EO = CO = AO\)，
\(\because ED = 4 + 4\sqrt 3 \)，
\(\therefore AO + \sqrt 3 AO = 4 + 4\sqrt 3 \)，
\(\therefore AO = 4\)，
\(\therefore AD = 8\)。

第356题

参考答案：①②④

第357题

如图，在\(\Delta ABC\)中，\(\angle ABC = 90^\circ \)，\(BD\)为\(AC\)边上的中线，过点\(C\)作\(CE \bot BD\)于点\(E\)，过点\(A\)作\(BD\)的平行线，交\(CE\)的延长线于点\(F\)，在\(AF\)的延长线上截取\(FG = BD\)，连接\(BG\)、\(DF\)．若\(AG = 13\)，\(BG = 5\)，则\(CF\)的长为___。

参考答案：6

第358题

参考答案：①③

第359题

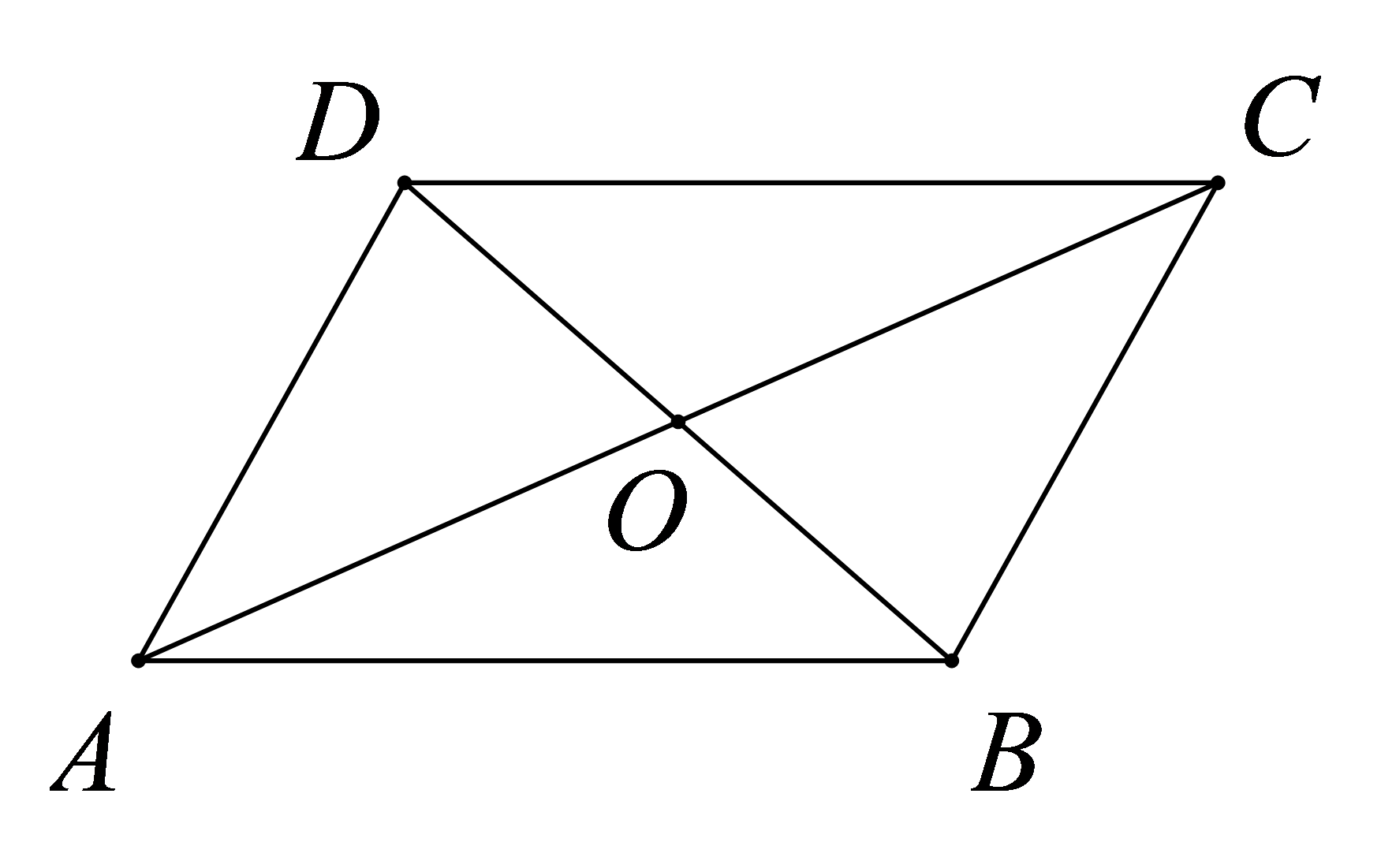
A.\(\angle A = \angle C\)

B.\(AB \bot BC\)

C.\(AC \bot BD\)

D.\(AC = BD\)

参考答案：C

第360题

已知，如图，\(\Delta ABC\)中，\(AD\)平分\(∠BAC\)交\(BC\)于点\(D\)，过点\(D\)分别作\(DE//AC\)交AB于点E，\(DF//AB\) 交\(AC\)于点\(F\)，证明四边形\(AEDF\)是菱形。

参考答案：证明：
\(\because DE//AC\)，\(DF//AB\)，
\(\therefore \)四边形\(AEDF\)是平行四边形，
\(\because AD\)平分\(\angle BAC\)，
\(\therefore \angle BAD = \angle CAD\)，
\(\because DF//AB\)，
\(\therefore \angle ADF = \angle BAD\)，
\(\therefore \angle CAD = \angle ADF\)，
\(\therefore AF = DF\)，
\(\therefore \)四边形\(AEDF\)是菱形。