初中数学八年级下册（648题）

---

如图，菱形\(ABCD\)的对角线\(AC\)与\(BD\)相交于点\(O\)，点\(E\)在\(BD\)上，连接\(AE\)，\(CE\)，\(\angle ABC = 60^\circ \)，\(\angle BCE = 15^\circ \)，\(ED = 4 + 4\sqrt 3 \)，求\(AD\)的长。

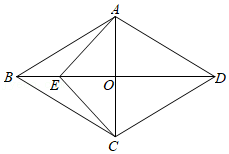
知识点：第十八章　平行四边形

参考答案：解：
\(\because \)四边形\(ABCD\)是菱形，\(\angle ABC = 60^\circ \)，
\(\therefore \angle ADC = 60^\circ \)，\(\angle BCD = 120^\circ \)，\(AC \bot BD\)，\(AO = CO\)，\(\angle ADB = \angle CDB = 30^\circ \)，\(\angle ACD = \angle ACB = 60^\circ \)，
\(\therefore DO = \sqrt 3 CO = \sqrt 3 AO\)，\(AD = 2AO\)，
\(\because \angle BCE = 15^\circ \)，
\(\therefore \angle ACE = 45^\circ \)，
\(\therefore \angle ACE = \angle DEC = 45^\circ \)，
\(\therefore EO = CO = AO\)，
\(\because ED = 4 + 4\sqrt 3 \)，
\(\therefore AO + \sqrt 3 AO = 4 + 4\sqrt 3 \)，
\(\therefore AO = 4\)，
\(\therefore AD = 8\)。