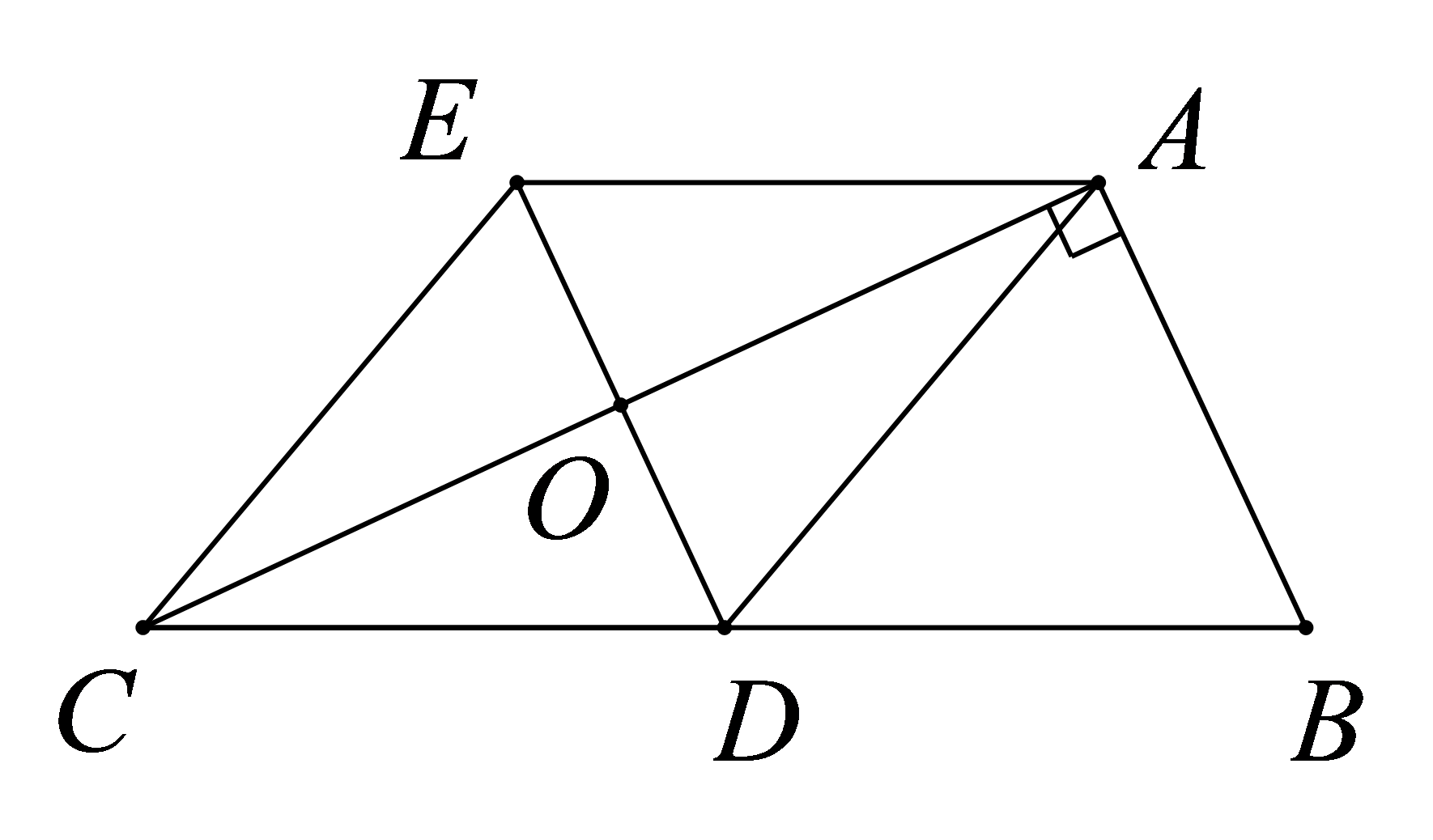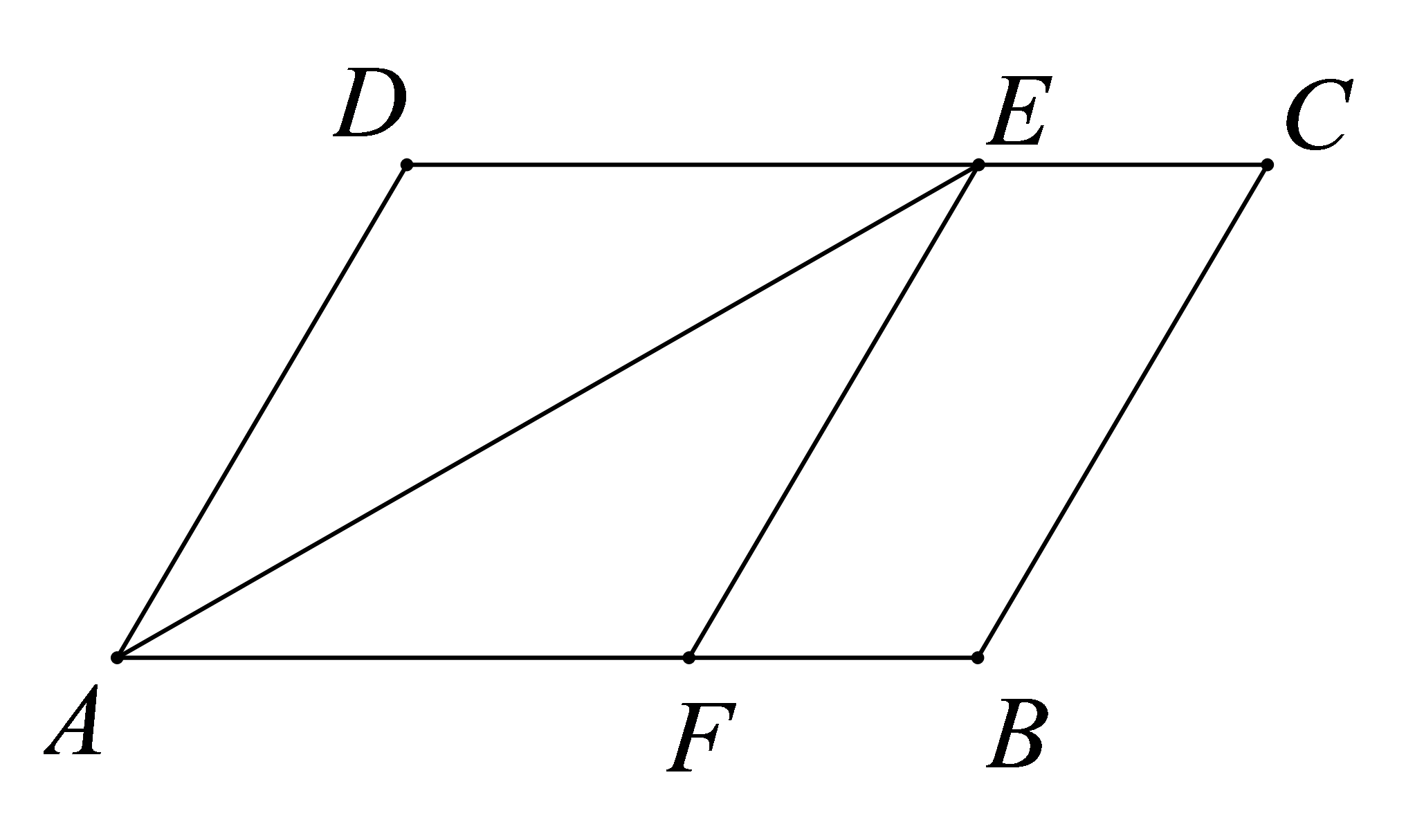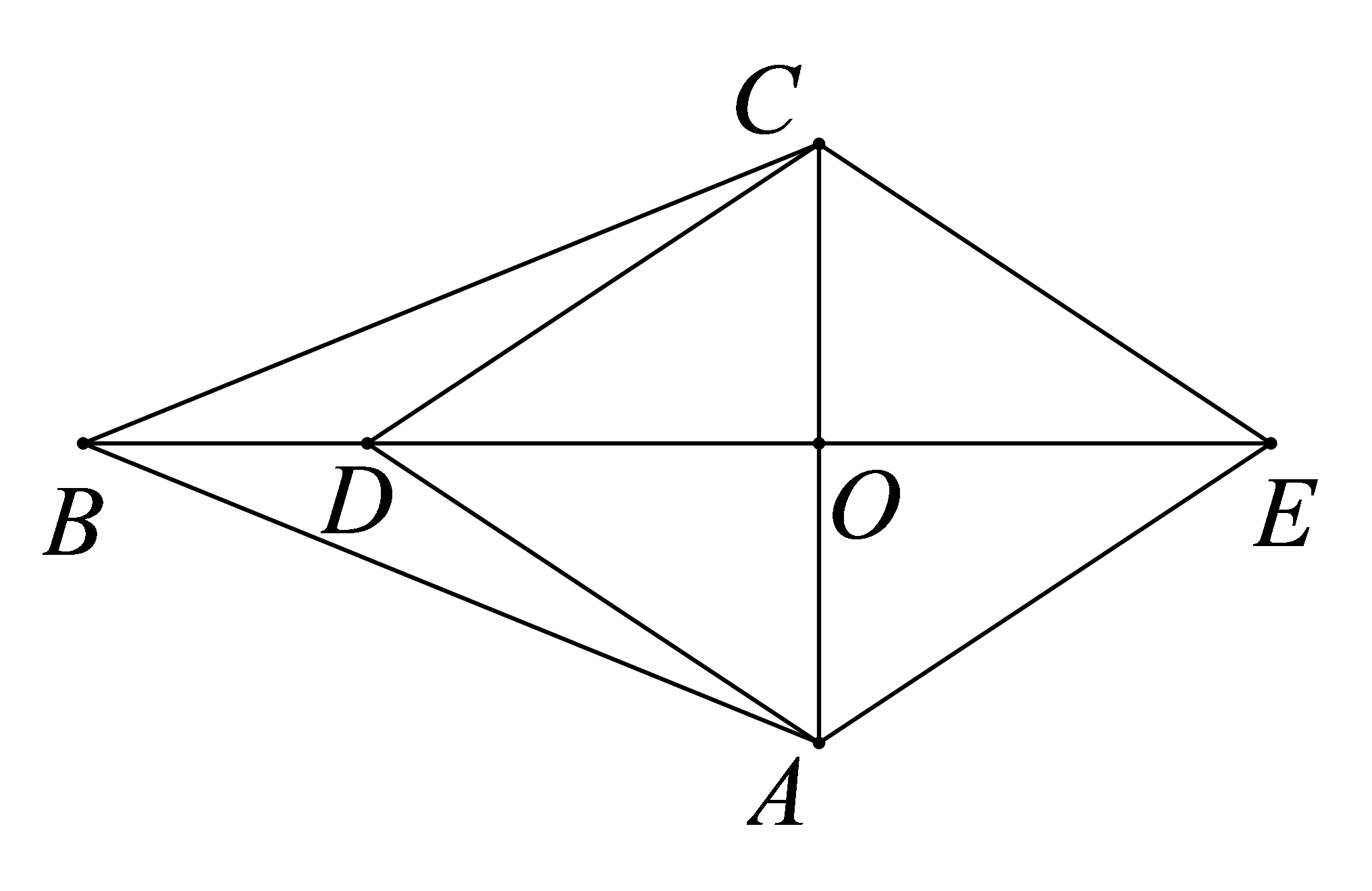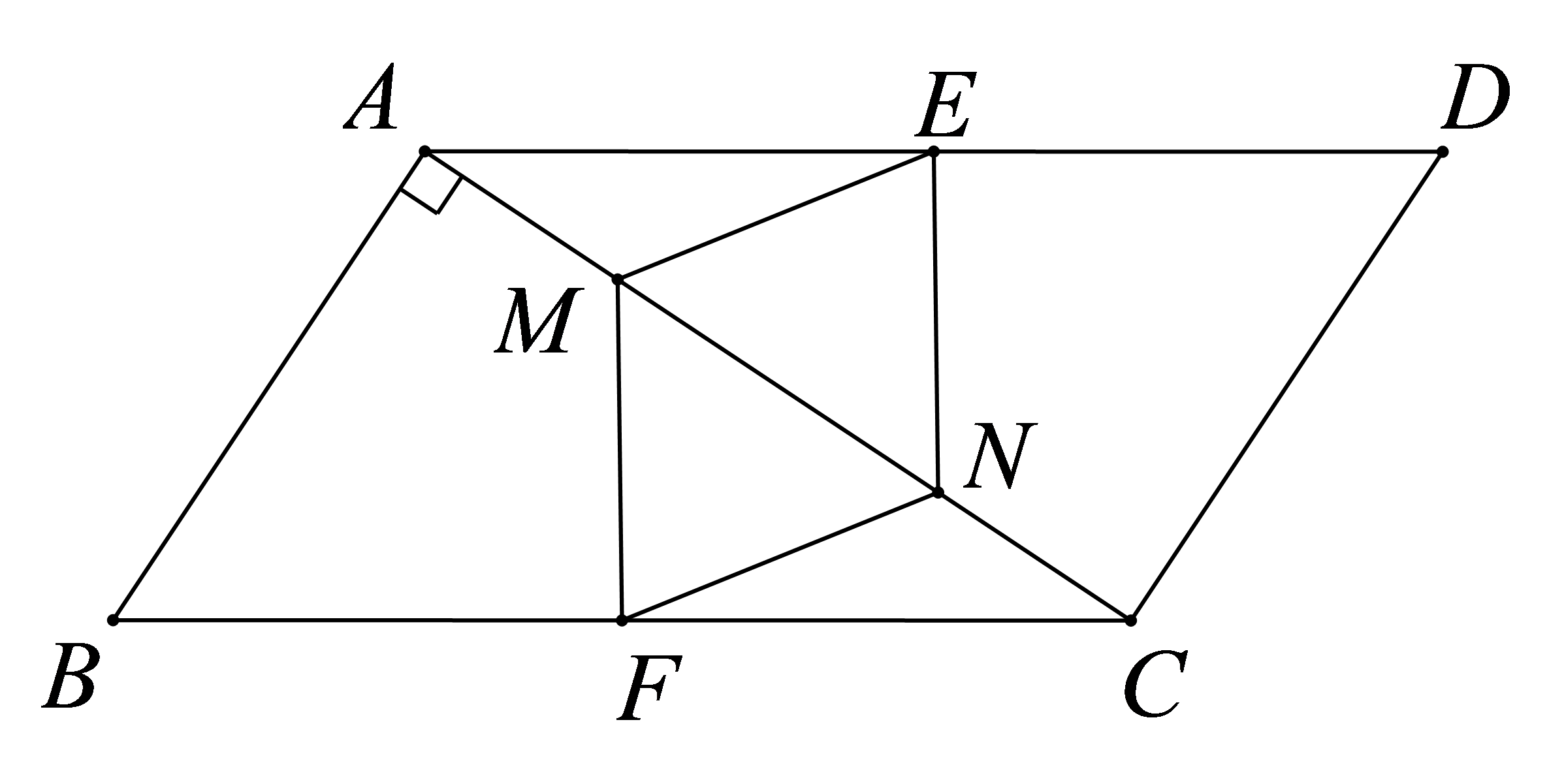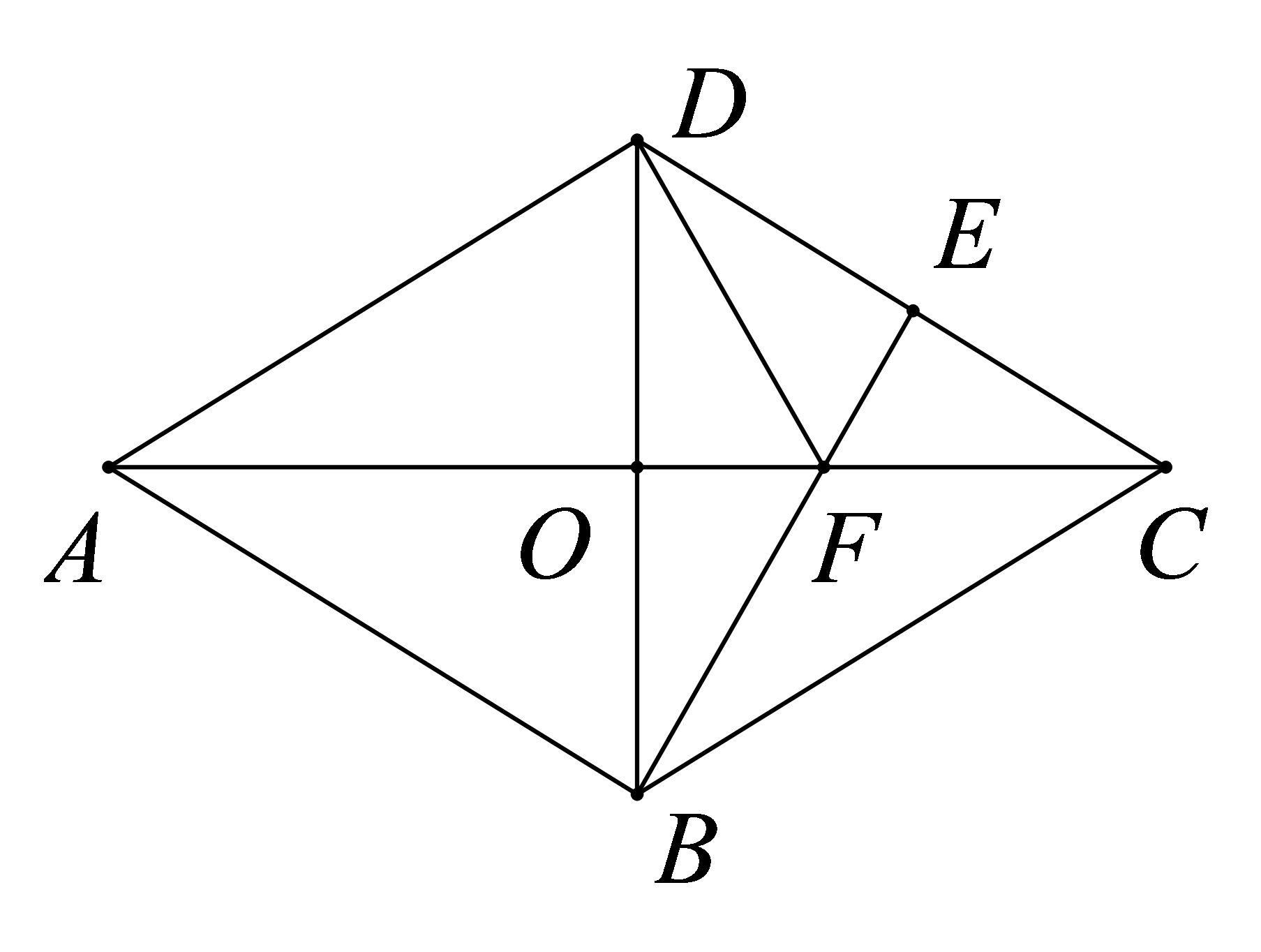“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
参考答案:证明: \(\because AE//BC\),\(DE//AB\),
\(\therefore \)四边形\(ABDE\)为平行四边形;
\(\therefore \)\(AE = BD\),
\(\because AD\)是边\(BC\)上的中线,
\(\therefore BD = CD\),
\(\therefore AE = CD\),
\(\because AE//CD\)
\(\therefore \)四边形\(ADCE\)是平行四边形,
又\(\because \angle BAC = 90^\circ \),\(AD\)是边\(BC\)上的中线,
\(\therefore AD = \frac{1}{2}BC = CD\),
\(\therefore \)平行四边形\(ADCE\)是菱形。
参考答案:证明:\(\because \)四边形\(ABCD\)是平行四边形,
\(\therefore AB//CD\),\(AD//BC\)
\(\therefore \angle DEA = \angle FAE\),
\(\because AE\)平分\(\angle BAD\),
\(\therefore \angle DAE = \angle FAE\),
\(\therefore \angle DEA = \angle DAE\),
\(\therefore AD = ED\),
\(\because EF//BC,AD//BC\)
\(\therefore EF//AD\) ,
\(\because DE//AF\)
\(\therefore \)四边形\(AFED\)是平行四边形,
又\(\because AD = ED\),
\(\therefore \)平行四边形\(AFED\)是菱形。
参考答案:证明:\(\because AB = BC\),\(BO \bot AC\),
\(\therefore AO = CO\),
又\(\because OE = OD\),
\(\therefore \)四边形\(ADCE\)是平行四边形,
\(\because DE⊥AC\),
\(\therefore \)平行四边形\(ADCE\)是菱形。
参考答案:证明:\(\because CE\)平分\(\angle ACB\),\(EF \bot BC\),\(\angle BAC = 90^\circ (EA \bot CA)\),
\(\therefore AE = EF\),\(∠ACE=∠BCE\)
\(\because AD \bot BC\),
\(\therefore \angle ADC = 90^\circ \),
\(\because \angle BAC = 90^\circ \),
\(\therefore \angle BCE + \angle CGD = 90^\circ \),\(\angle ACE + \angle AEC = 90^\circ \),
\(\therefore \angle CGD = \angle AEC\),
\(\because ∠CGD=∠AGE\),
\(\therefore \angle AGE = \angle AEC\)
\(\therefore AG=AE=EF\)
\(\because AD \bot BC\),\(EF \bot BC\),
\(\therefore AD//EF\),
即\(AG//EF\),\(AG = EF\),
\(\therefore \)四边形\(AEFG\)是平行四边形,
\(\because AE = EF\),
\(\therefore \)平行四边形\(AEFG\)是菱形。
参考答案:证明:\(\because \)四边形\(ABCD\)是平行四边形,\(O\)为对角线\(BD\)的中点,
\(\therefore BO = DO\),\(AD//BC\),
\(\therefore \)\(\angle EDB = \angle FBO\),
\(\because \)在\(\Delta EOD\)和\(\Delta FOB\)中,
\(\left\{ {\begin{array}{*{20}{l}} {\angle EDO = \angle FBO} \\ {OD = OB} \\ {\angle EOD = \angle FOB} \end{array}} \right.\),
\(\therefore \Delta DOE \cong \Delta BOF(ASA)\);
\(\therefore OE = OF\),
又\(\because OB = OD\),
\(\therefore \)四边形\(BEDF\)是平行四边形,
\(\because EF \bot BD\),
\(\therefore \)平行四边形\(BEDF\)为菱形。
第366题
如图,平行四边形ABCD的对角线\(AC\),\(BD\)相交于点\(O\),且\(AE//BD\),\(BE//AC\),\(OE = CD\),求证:四边形\(ABCD\)是菱形。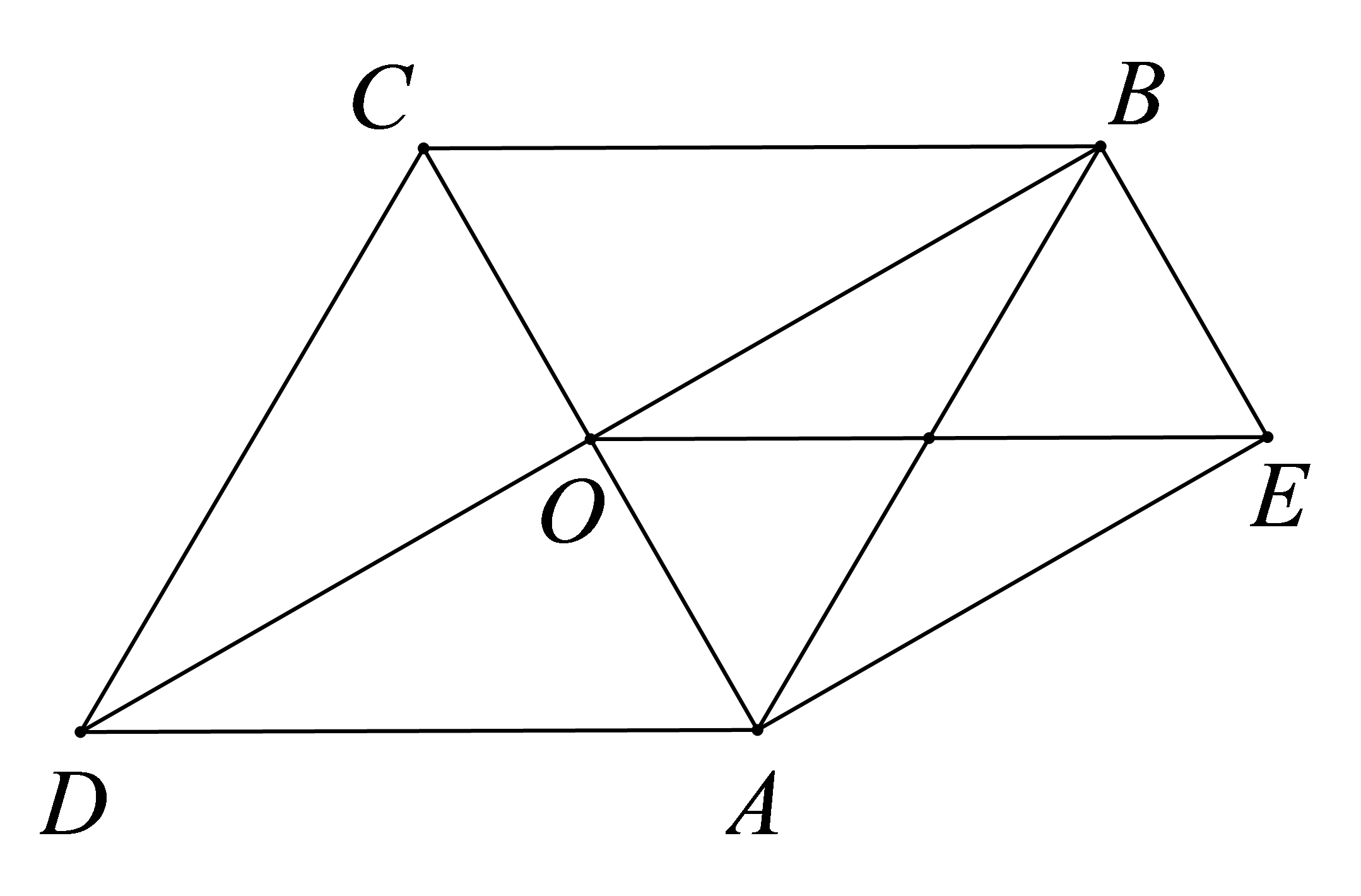
参考答案:证明:
\(\because AE//BD\),\(BE//AC\),
\(\therefore \)四边形\(AEBO\)是平行四边形,
\(\because \)四边形\(ABCD\)是平行四边形,
\(\therefore DC = AB\).
\(\because OE = CD\),
\(\therefore OE = AB\).
\(\therefore \)平行四边形\(AEBO\)是矩形,
\(\therefore \angle BOA = 90^\circ \).
\(\therefore AC \bot BD\).
\(\therefore \)平行四边形\(ABCD\)是菱形。
参考答案:
证明:连接
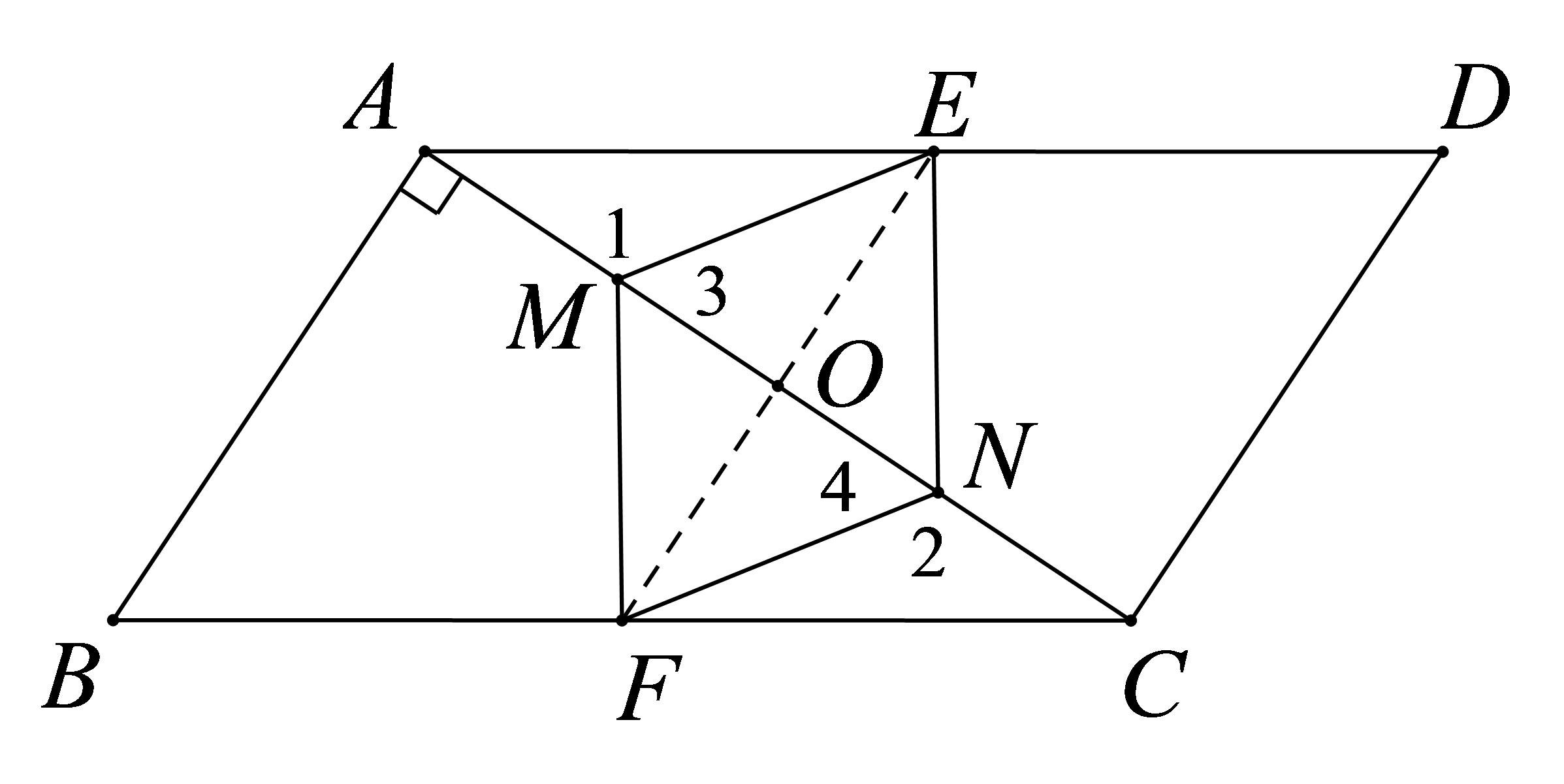
第368题
已知:如图,在四边形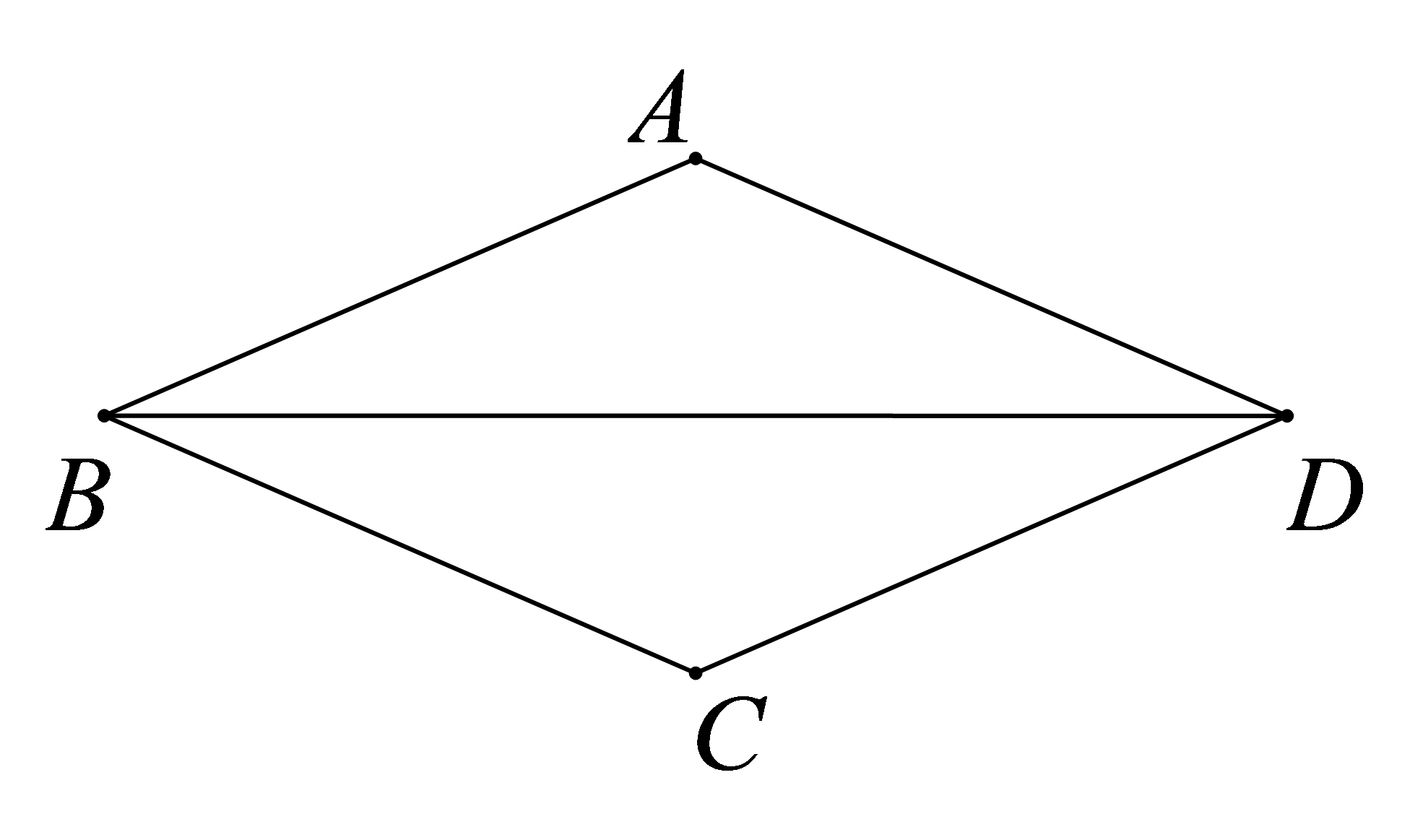
参考答案:证明:
\(\because BD\)平分\(\angle ABC\),
\(\therefore \angle ABD = \angle CBD\),
\(\because \)在\(\Delta ABD\)和\(\Delta CBD\)中\(\left\{ {\begin{array}{*{20}{l}}
{\angle ABD = \angle CBD} \\
{\angle A = \angle C} \\
{BD = BD}
\end{array}} \right.\),
\(\therefore \Delta ABD≌\Delta CBD(AAS)\),
\(\therefore AB = BC\),\(AD = DC\),
\(\because AB = AD\),
\(\therefore AB = BC = DC = AD\),
\(\therefore \)四边形\(ABCD\)是菱形。
参考答案:证明:\(\because AC\)是\(BD\)的垂直平分线,点\(F\)在\(AC\)上,
\(\therefore AB = AD\),\(BC = CD\),\(FD=FB\),
\(\because \)在\(\Delta ABF\)和\(\Delta ADF\)中,
\(\left\{ {\begin{array}{*{20}{l}} {AB = AD} \\ {FB = FD} \\ {AF = AF} \end{array}} \right.\),
\(\therefore \Delta ABF \cong \Delta ADF({\rm{SSS}})\),
\(\therefore \angle ABF = \angle ADF\),\(∠BAC=∠DAC\)
\(\because \angle BEC = \angle ADF\),
\(\therefore \angle BEC = \angle ABF\),
\(\therefore AB//CD\),
\(\therefore \angle BAC = \angle ACD\),
\(\therefore \angle DAC = \angle ACD\),
\(\therefore AD = CD\),
\(\because AB = AD\),\(BC = CD\),
\(\therefore AB = CB = CD = AD\),
\(\therefore \)四边形\(ABCD\)是菱形。
第370题
已知:如图,
A.\(120^\circ \)
B.\(135^\circ \)
C.\(145^\circ \)
D.\(150^\circ \)
参考答案:D
第371题
若正方形
A.\(\sqrt 2 \)
B.4
C.\(2\sqrt 2 \)
D.\(\frac{{\sqrt 2 }}{2}\)
参考答案:C
第372题
如图,四边形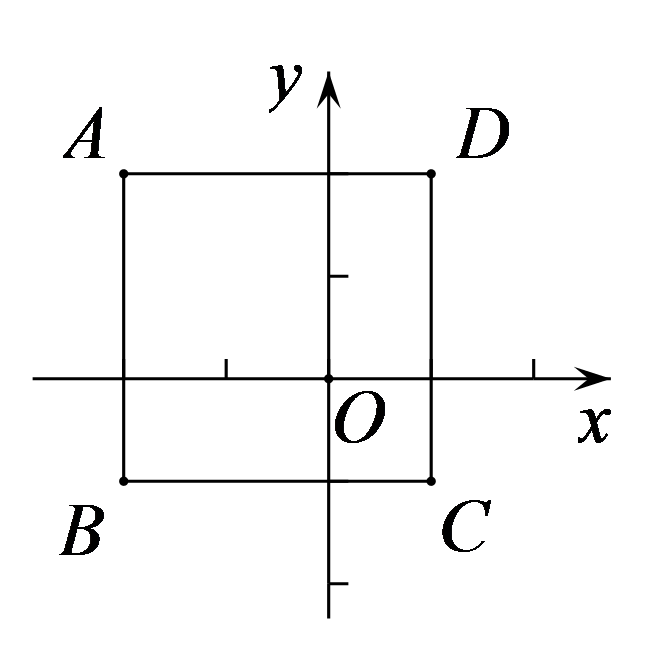
A.\(( - 1, - 2)\)
B.\(( - 1, - 3)\)
C.\(( - 2, - 1)\)
D.\(( - 3, - 1)\)
参考答案:C
第373题
如图,将正方形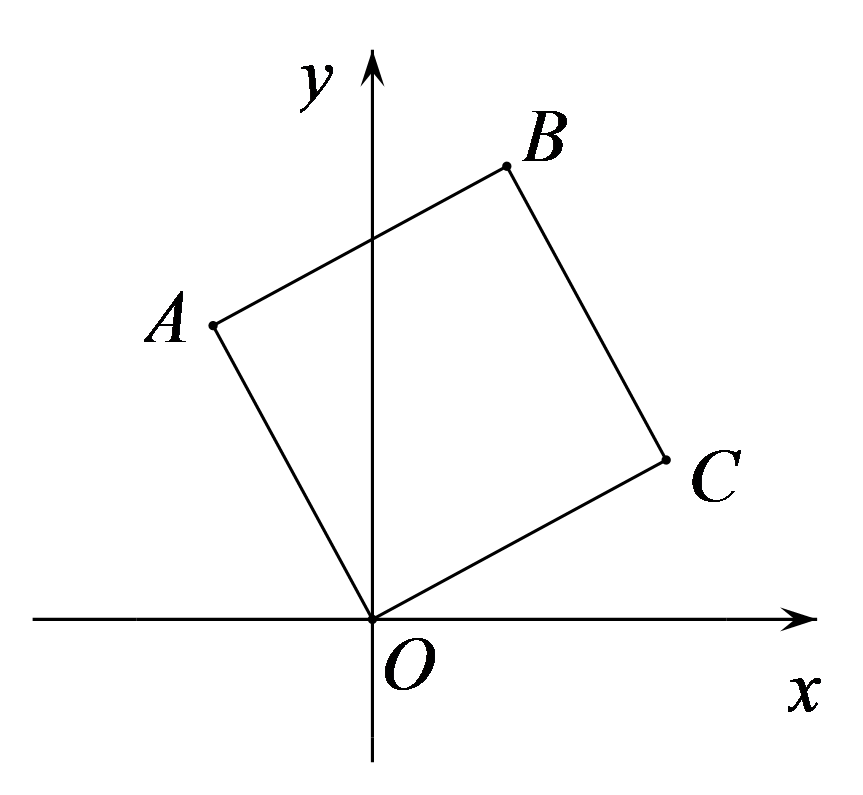
A.\((b,a)\)
B.\(( - b,a)\)
C.\((a, - b)\)
D.\(( - a,b)\)
参考答案:B
第375题
如图,正方形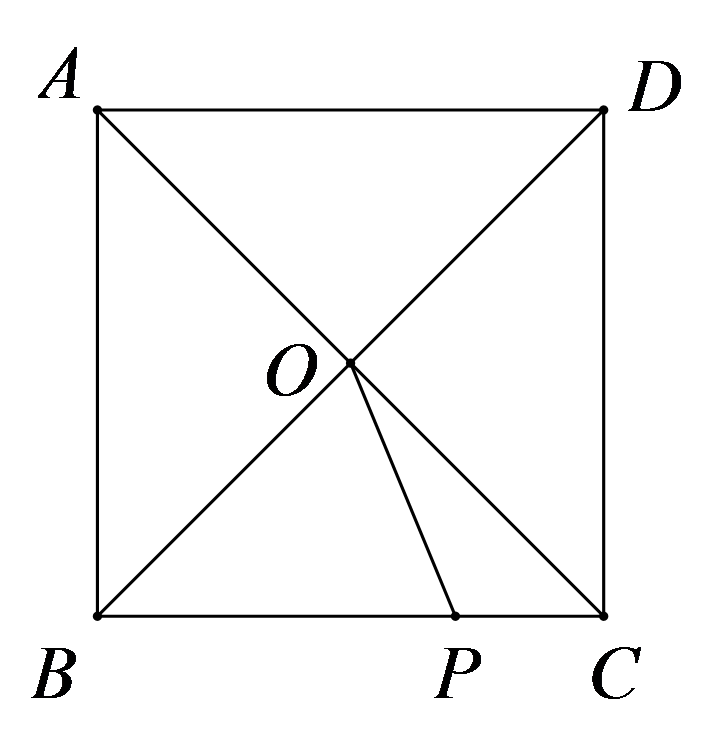
A.\(15^\circ \)
B.\(22.5^\circ \)
C.\(25^\circ \)
D.\(17.5^\circ \)
参考答案:B
第376题
如图,已知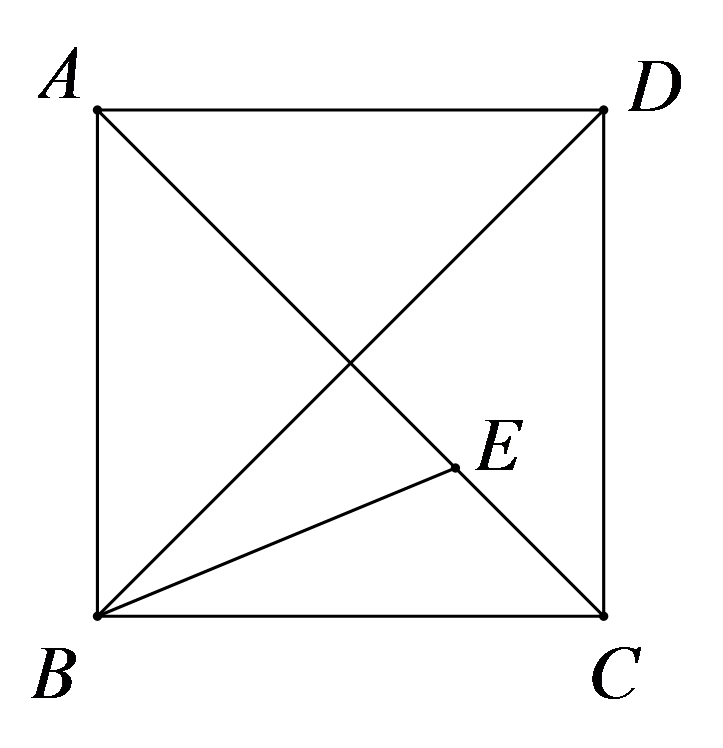
A.\(15^\circ \)
B.\(32.5^\circ \)
C.\(22.5^\circ \)
D.\(30^\circ \)
参考答案:C
A.\(2 + \sqrt 3 \)
B.\(2 + \frac{{\sqrt 3 }}{2}\)
C.\(\sqrt 3 + 1\)
D.\(2\sqrt 3 - 1\)
参考答案:C
第378题
如图,延长正方形\(ABCD\)的边\(BA\)至点\(E\),使\(AE = BD\),连接\(CE\),则\(\angle E\)为( )。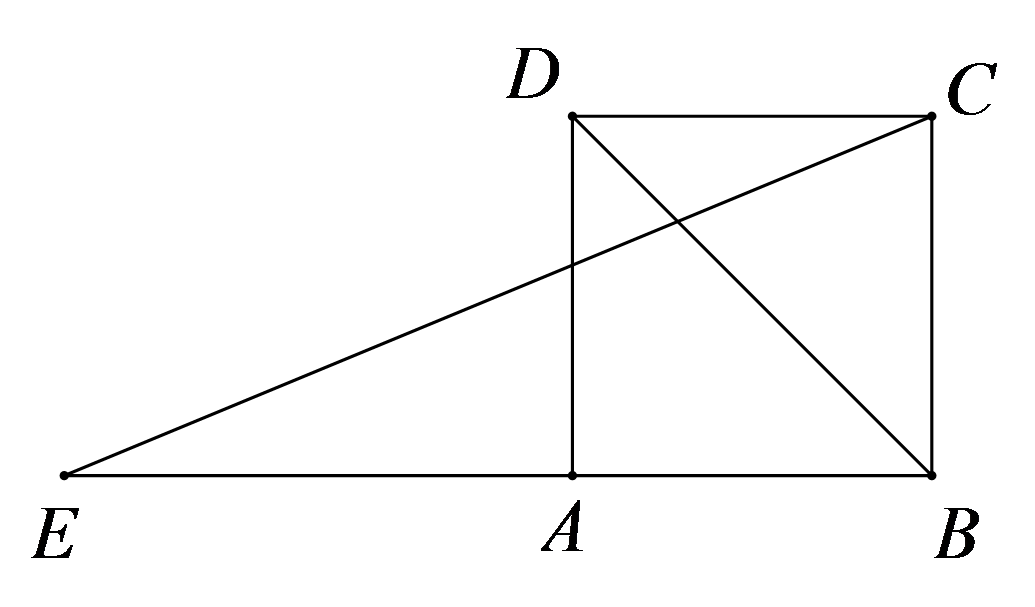
A.\(22.5^\circ \)
B.\(25^\circ \)
C.\(30^\circ \)
D.\(45^\circ \)
参考答案:A
A.\(30^\circ \)
B.\(79^\circ \)
C.\(22^\circ \)
D.\(81^\circ \)
参考答案:C
第380题
如图,正方形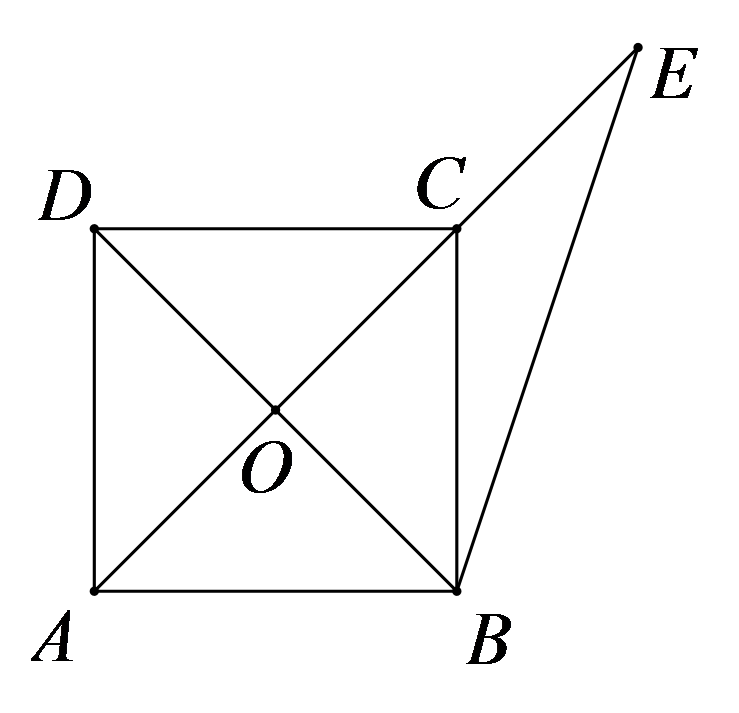
A.\(4\sqrt 2 \)
B.\(6\sqrt 2 \)
C.\(2\sqrt {10} \)
D.\(4\sqrt {10} \)
参考答案:C