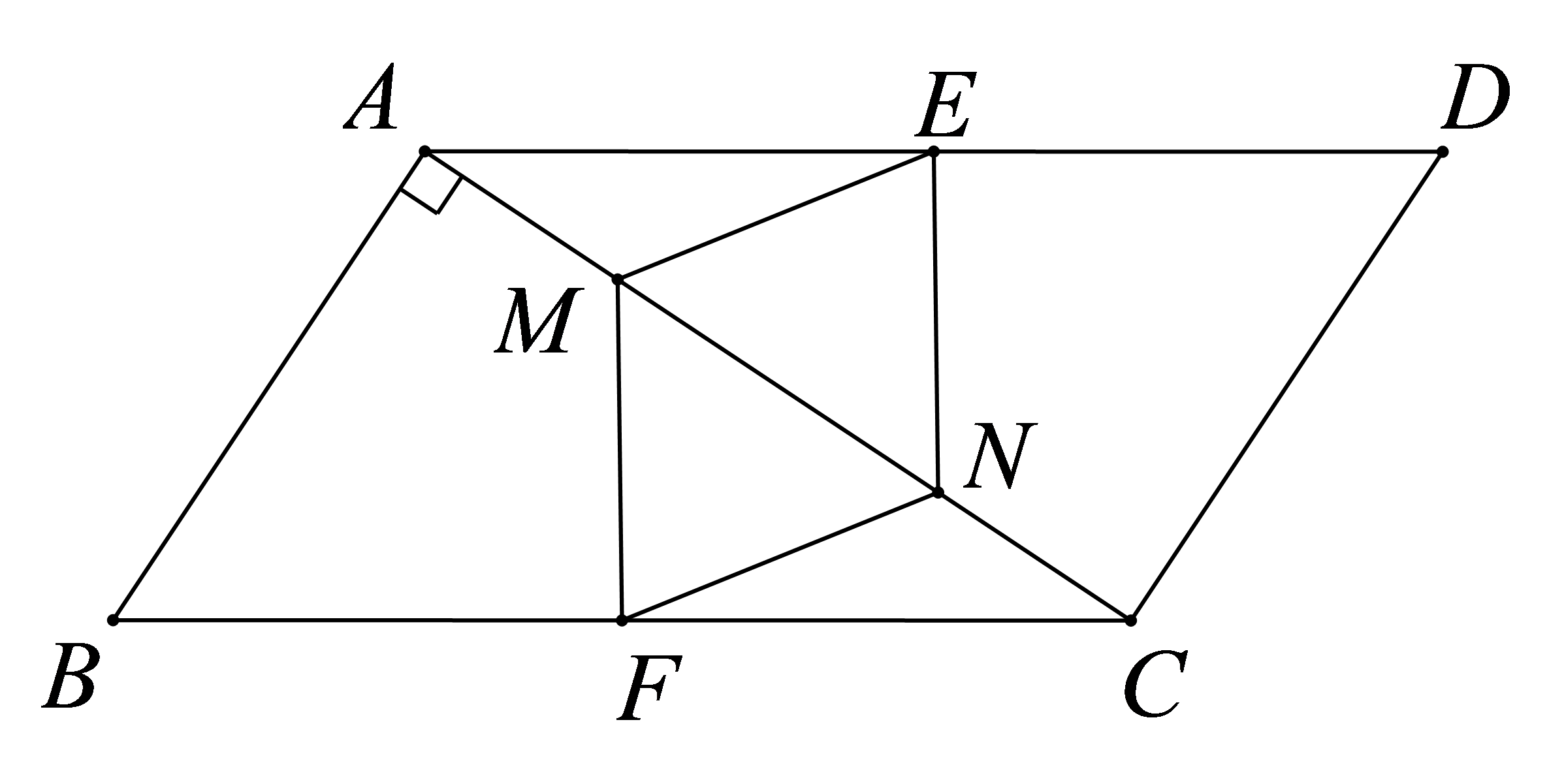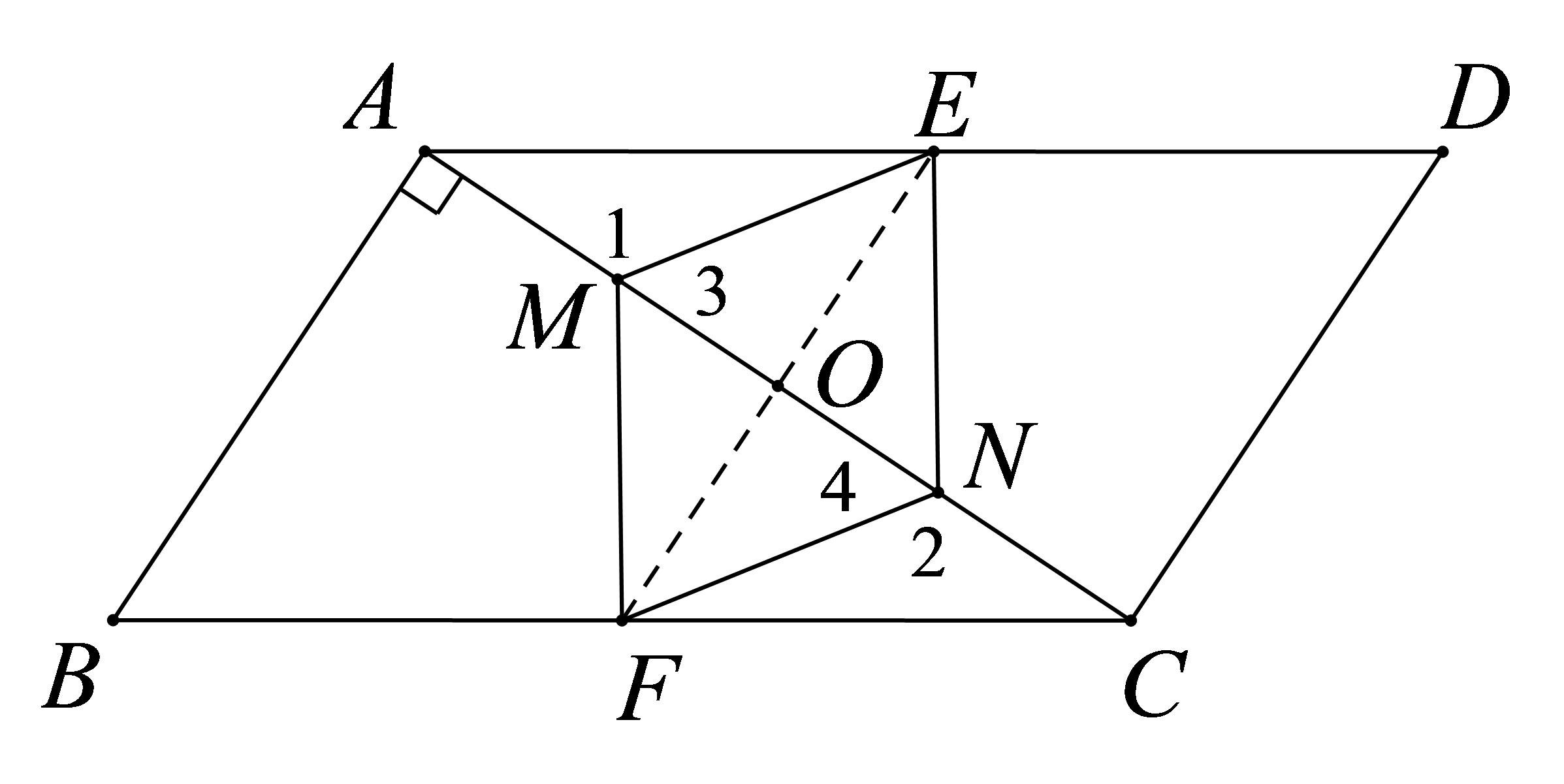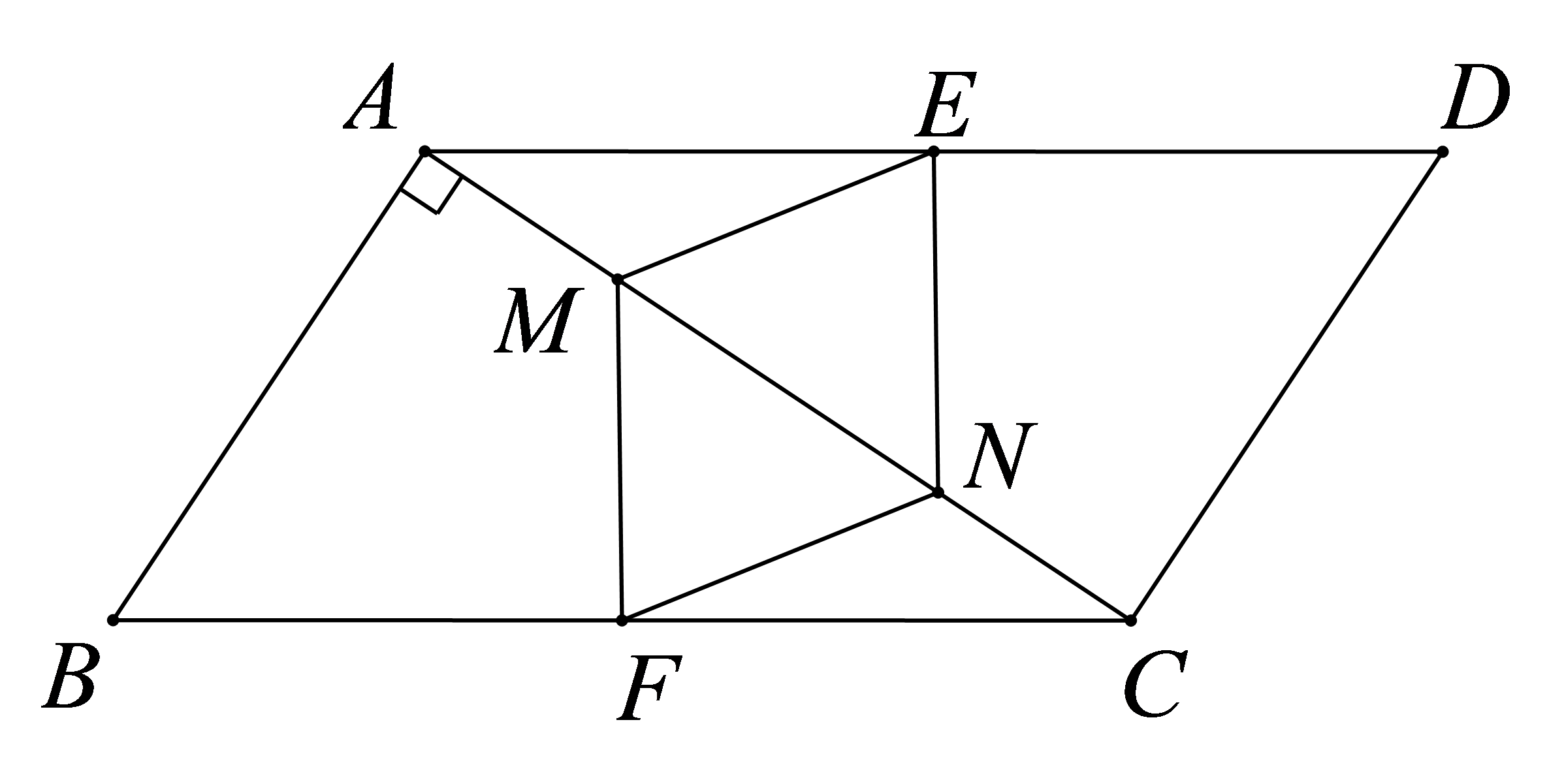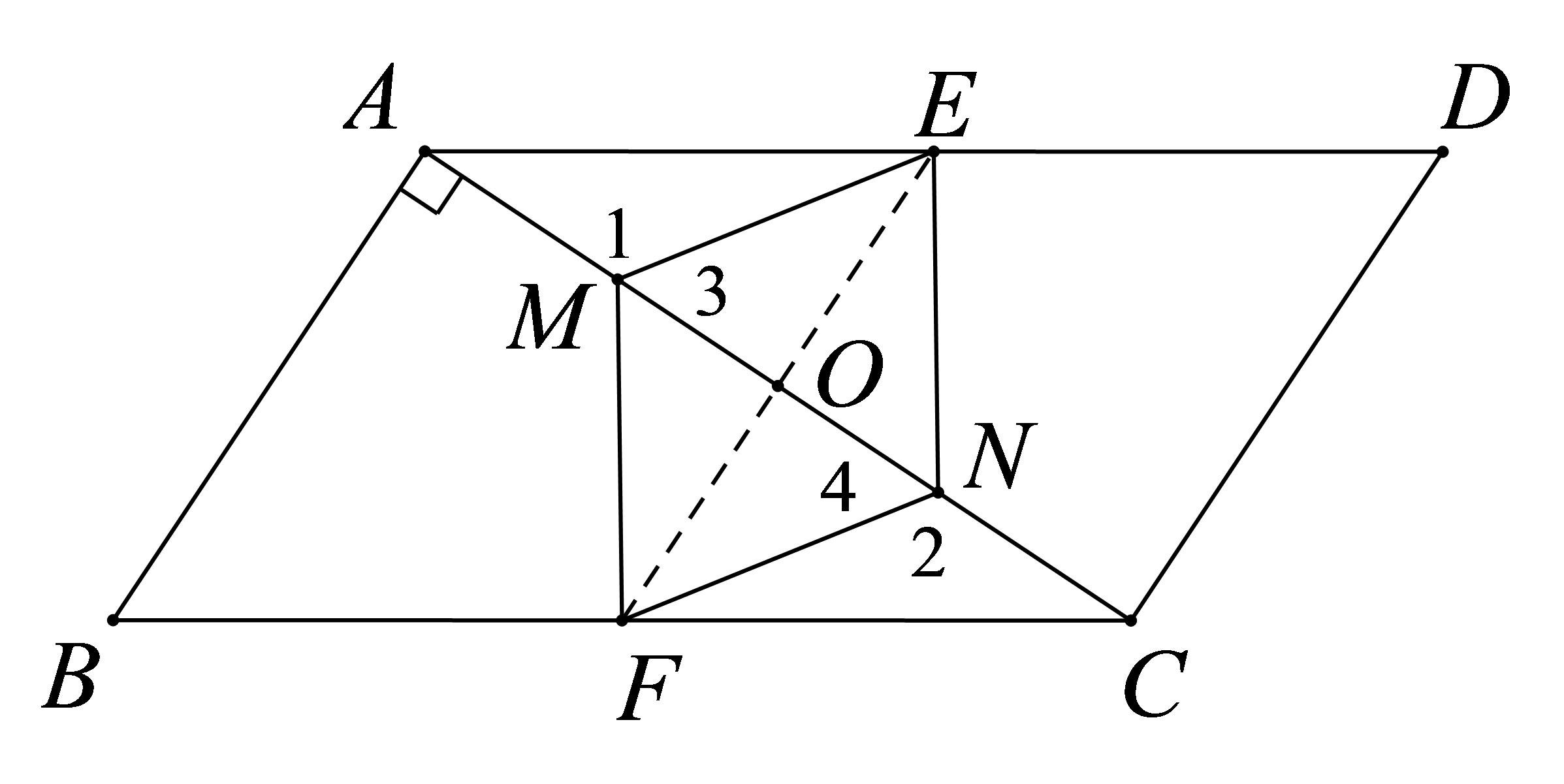证明：连接\(EF\)交\(AC\)于点\(O\)，

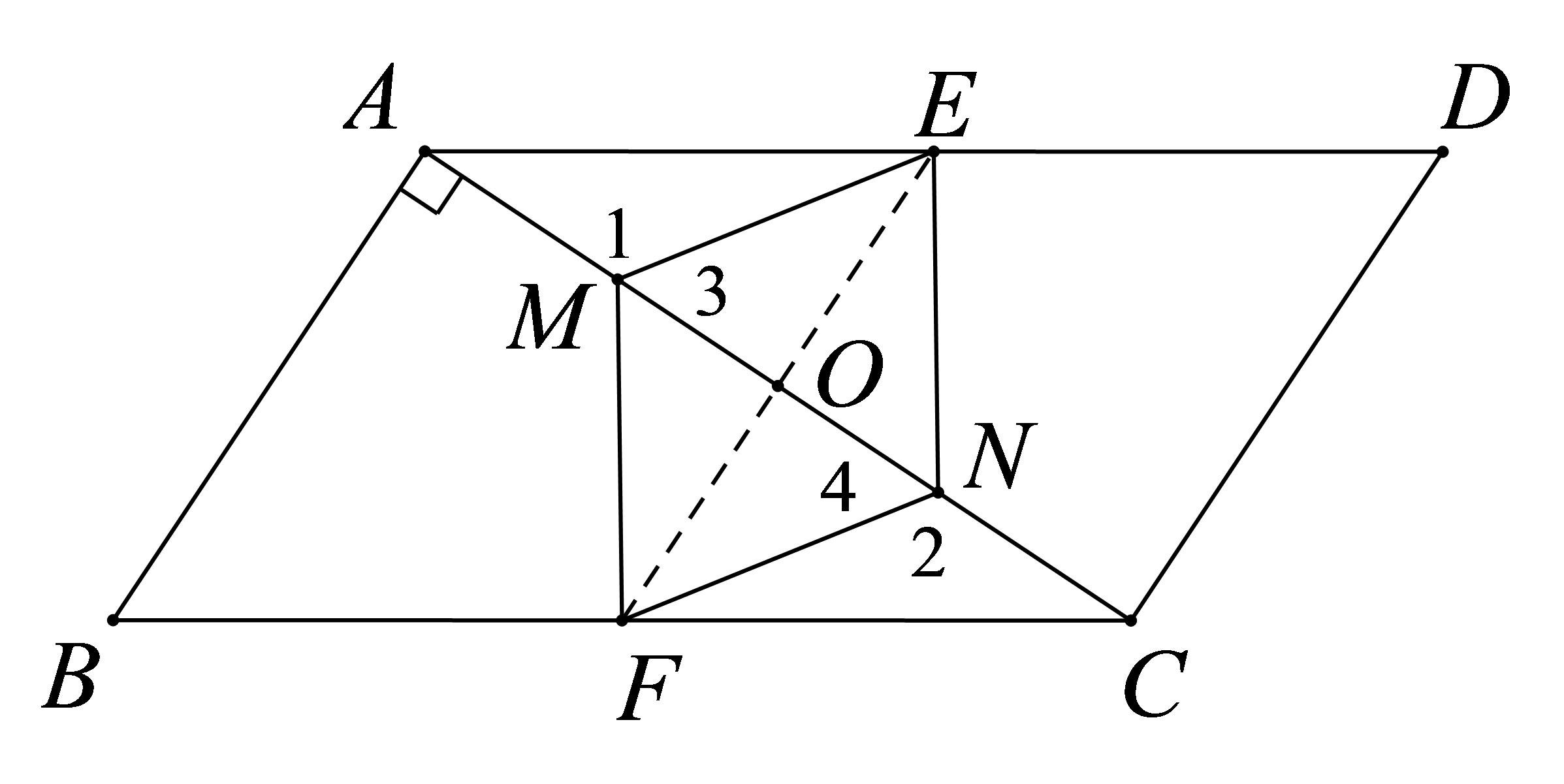
\(\because \)四边形\(ABCD\)是平行四边形，

\(\therefore AD//BC\)，\(AD = BC\)，

\(\therefore \angle EAM = \angle FCN\)，

\(\because E\)、\(F\)分别为\(AD\)、\(BC\)的中点，

\(\therefore AE = \frac{1}{2}AD,{\rm{ }}CF = BF = \frac{1}{2}BC\)，

\(\therefore AE=CF，AE=BF\)  

\(\because \)在\(\Delta AEM\)和\(\Delta CFN\)中，

\(\left\{ {\begin{array}{*{20}{l}} {AE = CF} \\ {\angle EAM = \angle FCN} \\ {AM = CN} \end{array}} \right.\)，

\(\therefore \Delta AEM \cong \Delta CFN(SAS)\)，

\(\therefore EM = FN\)，\(∠1=∠2\)，

\(\therefore ∠3=∠4\)，

\(\therefore EM//FN\)，

\(\therefore \)四边形\(EMFN\)是平行四边形；

\(\because \)\(AE//BF\)，\(AE = BF\)，

\(\therefore \)四边形\(AEFB\)是平行四边形，

\(\therefore AB//EF\)，

\(\because ∠BAC=90°\)，

\(\therefore \angle COF = \angle BAC = 90^\circ \)，

\(\therefore EF \bot MN\)，

\(\therefore \)平行四边形\(EMFN\)是菱形。

进入考试题库