初中数学八年级下册（648题）

---

如图，在\(\Delta ABC\)中，\(\angle BAC = 90^\circ \)，\(AD \bot BC\)于\(D\)，\(CE\)平分\(\angle ACB\)，交\(AB\)于点\(E\)，交\(AD\)于点\(G\)， \(EF \bot BC\)于点\(F\)，连接FG，求证：四边形\(AEFG\)是菱形。

    

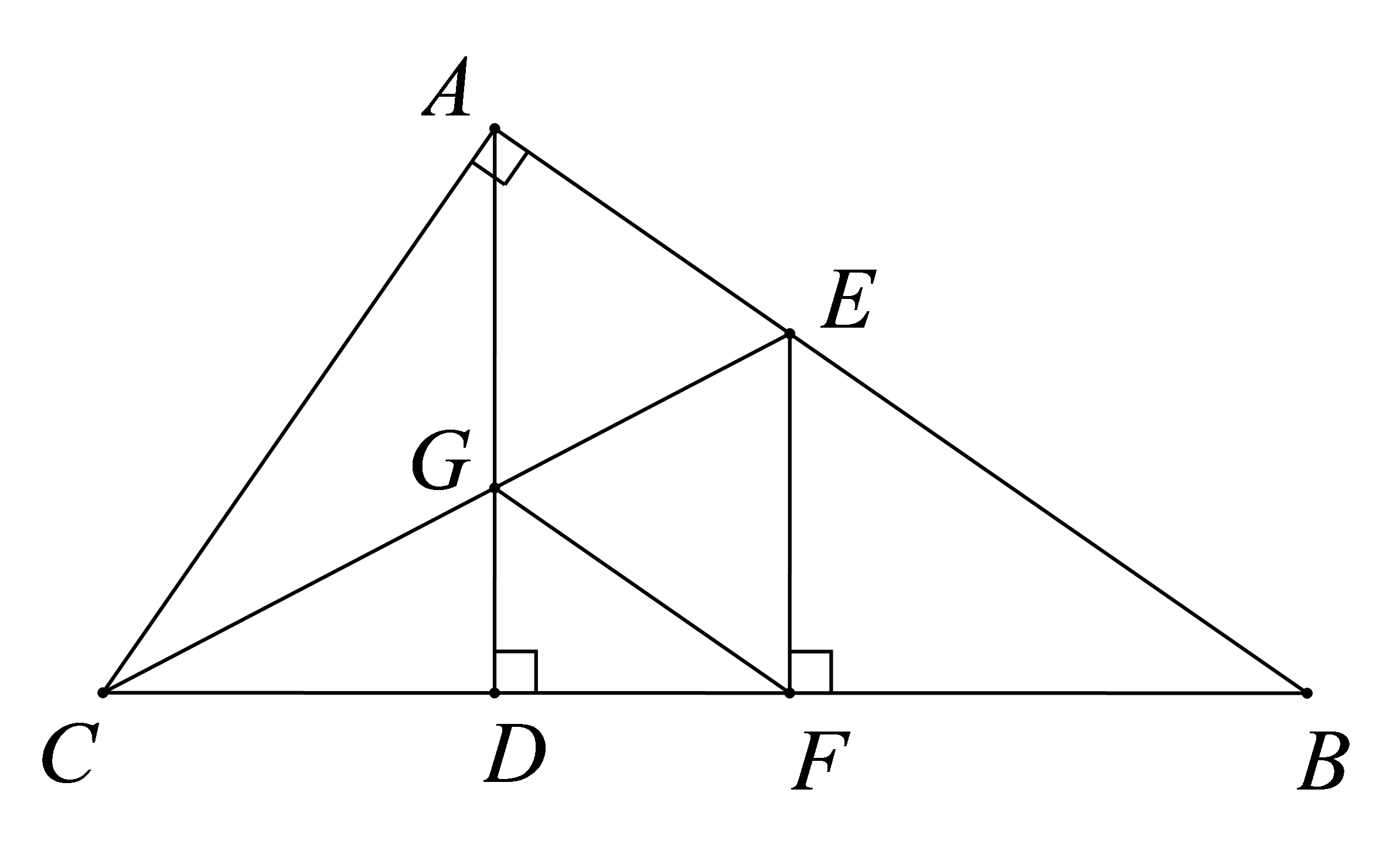
知识点：第十八章　平行四边形

参考答案：证明：\(\because CE\)平分\(\angle ACB\)，\(EF \bot BC\)，\(\angle BAC = 90^\circ (EA \bot CA)\)，

\(\therefore AE = EF\)，\(∠ACE=∠BCE\)

\(\because AD \bot BC\)，

\(\therefore \angle ADC = 90^\circ \)，

\(\because \angle BAC = 90^\circ \)，

\(\therefore \angle BCE + \angle CGD = 90^\circ \)，\(\angle ACE + \angle AEC = 90^\circ \)，

\(\therefore \angle CGD = \angle AEC\)，

\(\because ∠CGD=∠AGE\)，

\(\therefore \angle AGE = \angle AEC\)

\(\therefore AG=AE=EF\)

\(\because AD \bot BC\)，\(EF \bot BC\)，

\(\therefore AD//EF\)，

即\(AG//EF\)，\(AG = EF\)，

\(\therefore \)四边形\(AEFG\)是平行四边形，

\(\because AE = EF\)，

\(\therefore \)平行四边形\(AEFG\)是菱形。