初中数学八年级下册（648题）

---

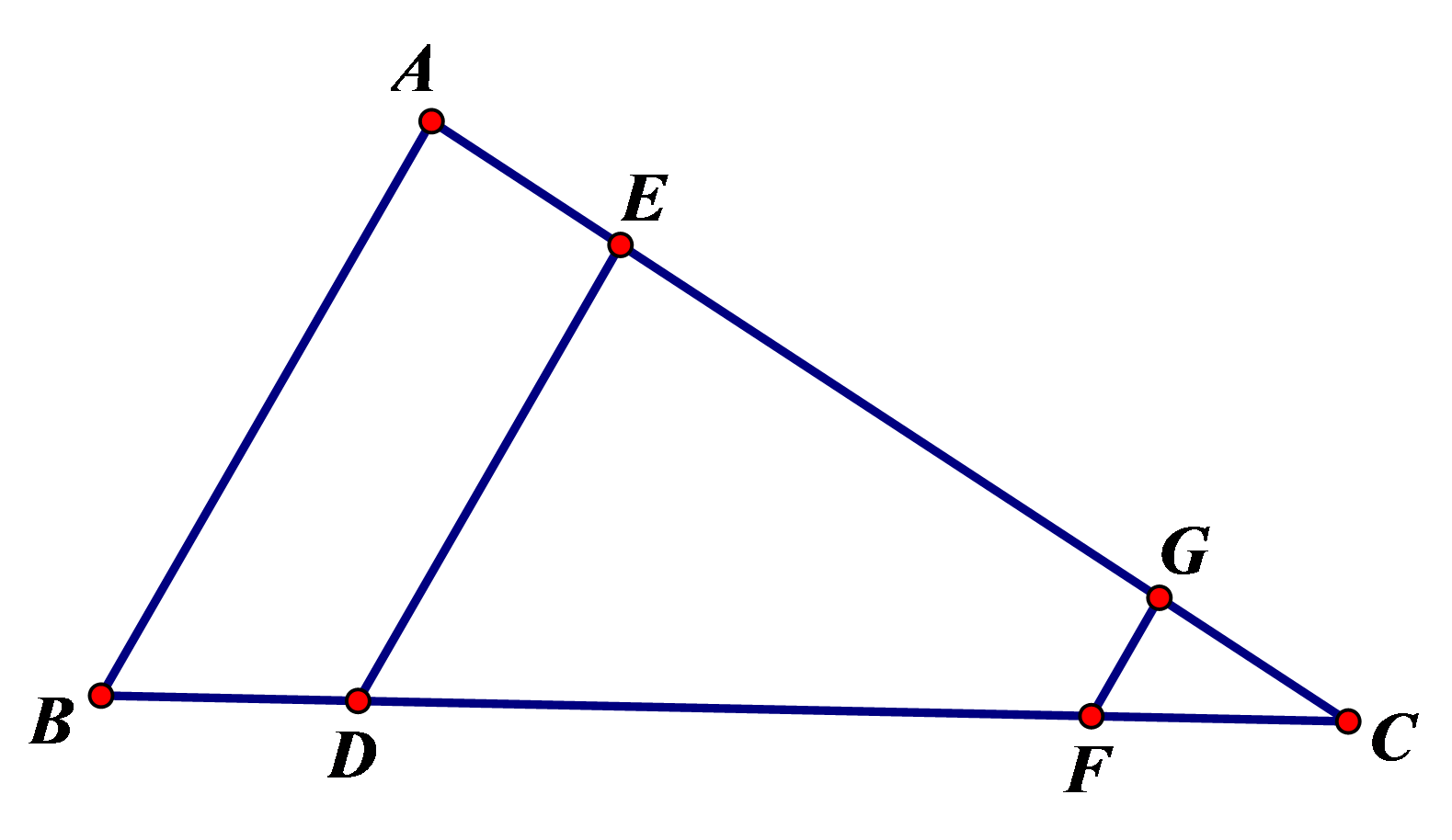
如图，在\( △ABC\)中，点\( E，G\)在\( AC\)边上，点\( D，F\)在\( BC\)边上，且\( BD=CF，\mathrm{ }AB//DE//FG\).

求证：\( AB=DE+FG\)。

    

知识点：第十八章　平行四边形

参考答案：

证明：如图，在\( AB\)上截取一点\( H\)，使\( AH=DE\)，连接\( DH\)。

\( \because AB//DE，\therefore AH//DE\)，又\( \because AH=DE\)，∴四边形\( HDEA\)为平行四边形，\( \therefore AE//DH，\therefore AC//DH\)。

\( \because AB//FG，\mathrm{ }\therefore \mathrm{\angle }GFC=\mathrm{\angle }B\)，又\( \because AC//DH，\therefore \mathrm{\angle }BDH=\mathrm{\angle }C\)。

在\( △BHD\)和\( △FGC\)中\( \mathrm{\angle }B=\mathrm{\angle }GFC，BD=CF，\mathrm{\angle }BDH=\mathrm{\angle }C，\)\(\therefore △BHD≌△FGC\mathrm{ }（\mathrm{A}\mathrm{S}\mathrm{A}）\)

\( \therefore BH=FG，\therefore AB=AH+BH=DE+FG\)。