初中数学八年级下册（648题）

---

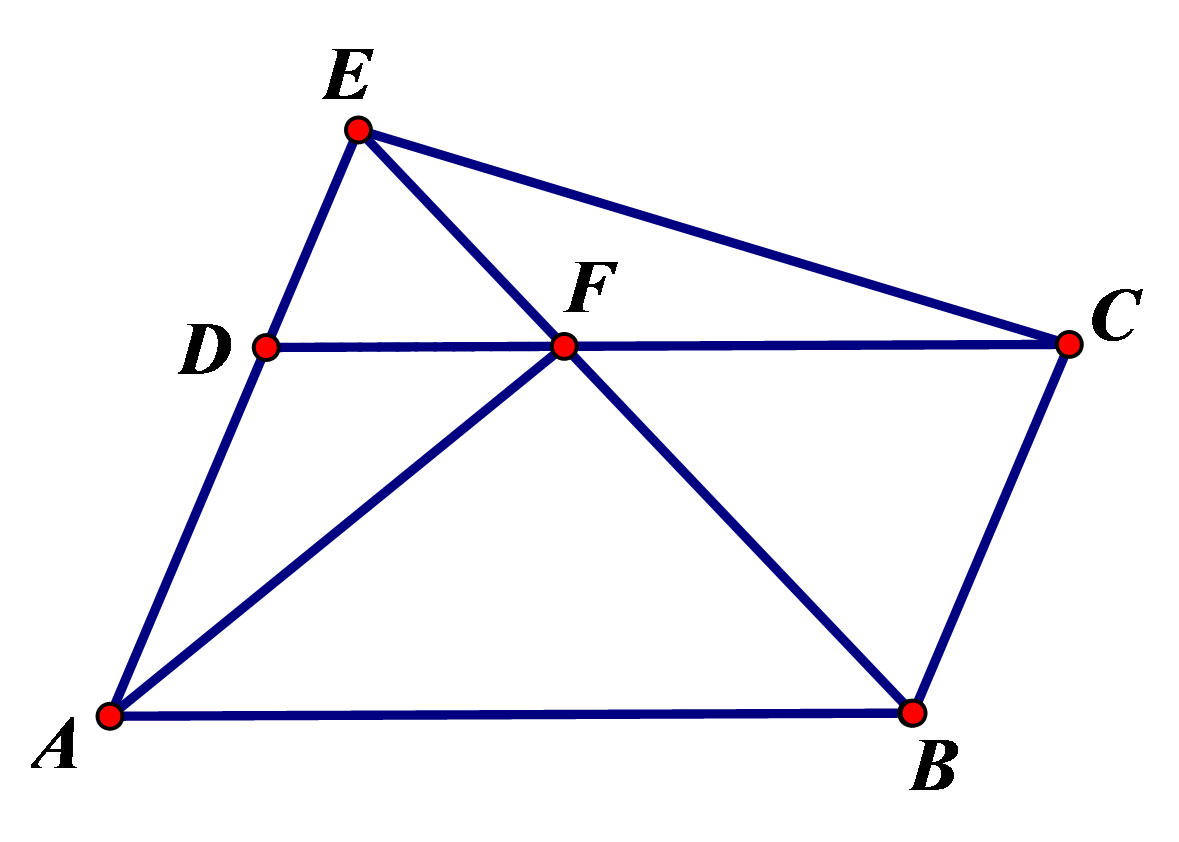
如图，\( E\)是\(▱ABCD\)的边\( AD\)延长线上一点，\( BE\)交\( DC\)于\( F\)。求证：\( {S}_{△ADF}＝{S}_{△EFC}\)。

知识点：第十八章　平行四边形

参考答案：\(\because ▱ABCD\mathrm{}，\)
\(\therefore AB//CD，AD//BC，\)
\(\therefore AB//CD，\mathrm{}AE//BC\mathrm{}\)

连接\( BD\)

\( \therefore {S}_{△BDF}＝{S}_{△ADF}，\)
\(\because {S}_{△BCE}＝{S}_{△BCD}，\)
\(\therefore {S}_{△CFE}＝{S}_{△BFD}，\)
\(\therefore {S}_{△FDB}＝{S}_{△FDA}\)。