第281题

参考答案：\(\frac{{\sqrt 2 }}{3}{\rm{\pi }}\)。

第282题

参考答案：证明：设\(AD = \sqrt 2 a\)，则\(AC = 2a\)，

\(\because \angle ACD = 45^\circ \)，

在\(\Delta ACD\)中，由余弦定理知，\(A{D^2} = A{C^2} + C{D^2} - 2AC \cdot CD\cos \angle ACD\)，

\(\therefore 2{a^2} = 4{a^2} + C{D^2} - 2 \cdot 2a \cdot CD \cdot \frac{{\sqrt 2 }}{2}\)，解得\(CD = \sqrt 2 a\)，

\(\therefore A{D^2} + C{D^2} = A{C^2}\)，即\(AD\bot CD\)，

又平面\(ACFD\bot 平面DBC\)，平面\(ACFD∩平面DBC=CD\)，\(AD\subset 平面ACFD，\)

∴\(AD⊥\)平面\(DBC\)，

\(\because BC \subset \)平面\(DBC\)，

\(\therefore AD \bot BC\)；

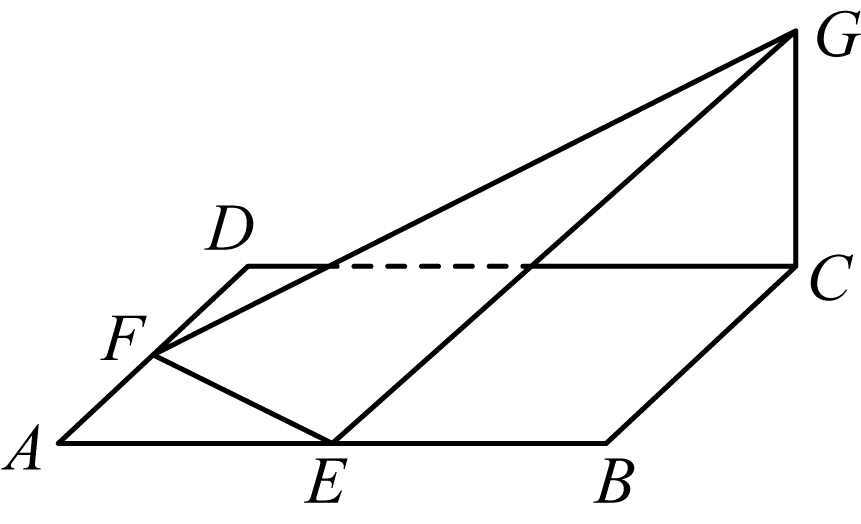
第283题

参考答案：解：由三棱台的性质知，\(DE\)||\(AB\)，

故直线\(DE\)与平面\(DBC\)所成角即为直线\(AB\)与平面\(DBC\)所成角．

由（1）知，\(AD \bot \)平面\(DBC\)，

\(\therefore \angle ABD\)即为所求．

\(\because AD = \sqrt 2 BC\)，\(AD = \sqrt 2 a\)，\(\therefore BC = a\)，

在\(\Delta ABC\)中，由余弦定理知，\(A{B^2} = A{C^2} + B{C^2} - 2AC\bullet BC\cos \angle ACB = 4{a^2} + {a^2} - 2\bullet 2a\bullet a\bullet \frac{1}{2} = 3{a^2}\)，\(\therefore AB = \sqrt 3 a\)，

在\({\rm{Rt}}\Delta {\rm{ABD}}\)中，\(\sin \angle ABD = \frac{{AD}}{{AB}} = \frac{{\sqrt 2 a}}{{\sqrt 3 a}} = \frac{{\sqrt 6 }}{3}\)．

故直线\(DE\)与平面\(DBC\)所成角的正弦值为\(\frac{{\sqrt 6 }}{3}\)．

`

第284题

参考答案：证明：由题意知，四边形\(ABCD\)为等腰梯形，

且\(AB = 2a\)，\(BC = a\)，\(\angle ABC = {60^0}\)，

由余弦定理，

\(AC = \sqrt {A{B^2} + B{C^2} - 2 \cdot AB \cdot BC \cdot \cos {{60}^0}} = \sqrt 3 a\)，

则\(A{B^2} + B{C^2} = A{B^2}\)，

所以\(AC \bot BC\)。

又因为平面\(ACEF \bot \)平面\(ABCD\)，\(BC \subset \)平面\(ABCD\)，平面\(ACEF \cap \)平面\(ABCD = AC\)，

所以\(BC \bot \)平面\(ACEF\)；

第285题

参考答案：存在，\(FM = \frac{{\sqrt 3 }}{3}a\)

第286题

参考答案：证明：
因为平面\(ABC \bot \)平面\(ABD\)，
平面\(ABC \cap \)平面\(ABD\)＝\(AB\)，
\(AD \bot AB\)，
所以\(AD \bot \)平面\(ABC\)，
因为\(BC \subset \)平面\(ABC\)，
所以\(AD \bot BC\)；

第287题

参考答案：\(\frac{{\sqrt {13} }}{{26}}\)

第288题

参考答案：证明：由题意，\(AB \bot BE\)，得\(AP \bot PE\)，同理，\(DP \bot PE\)。

又因为\(AP \cap DP = P\)，

所以\(PE \bot \)平面\(PAD\)。

又因为\(PE \subset \)平面\(PDE\)，

所以平面\(PDE \bot \)平面\(PAD\)。

第289题

参考答案：45°

第290题

参考答案：\(\frac{{2\sqrt {11} }}{{11}}\)

第291题

参考答案：证明：
因为\(AB = AD\)，\(O\)为\(BD\)的中点，
所以\(AO \bot BD\)。
因为平面\(ABD \cap \)平面\(BCD = BD\)，
平面\(ABD \bot \)平面\(BCD\)，
\(AO \subset \)平面\(ABD\)，
所以\(AO \bot \)平面\(BCD\)，
因为\(CD \subset \)平面\(BCD\)，
所以\(OA \bot CD\)；

第292题

参考答案：\(\frac{{\sqrt 3 }}{6}\)

第293题

A.三个点确定一个平面

B.一条直线和一个点确定一个平面

C.圆心和圆上两点可确定一个平面

D.梯形可确定一个平面

参考答案：D

第294题

参考答案：平行或相交。

第295题

A.内心

B.外心

C.重心

D.垂心

参考答案：B

第296题

参考答案：证明：
∵D，E分别是AB，PB的中点，
∴DE||PA．
又∵DE\( \not\subset \)平面PAC，PA\( \subset \)平面PAC，
∴DE||平面PAC；

解析：

请查看本题第一问视频解析

第297题

参考答案：证明：
∵PC⊥平面ABC，AB\( \subset \)平面ABC，
∴PC⊥AB．

∵AB⊥BC，PC\( \cap \)BC=C，PC\( \subset \)平面PBC，BC\( \subset \)平面PBC，
∴AB⊥平面PBC．

又∵PB\( \subset \)平面PBC，
∴AB⊥PB．

第298题

参考答案：证明：∵M是PD的中点，△PAD为正三角形，∴AM⊥PD．

又∵侧面PAD⊥底面ABCD，底面ABCD为正方形，∴CD⊥AD，CD⊥平面PAD，AM\( \subset \)平面PAD，∴CD⊥AM．

CD\( \cap \)PD=D，CD\( \subset \)平面PCD，PD\( \subset \)平面PCD，∴AM⊥平面PCD；

第299题

参考答案：

第300题

参考答案：用抽签法抽取10名文科生:
①将80名文科学生依次编号为：1，2，3，\( \cdot \cdot \cdot \)80；
②将号码分别写在形状、大小均相同的纸片上，制成号签；
③把80个号签放入一个不透明的容器 ，搅拌均匀，每次从中不放回地抽取一个号签，连续抽取10次；
④与号签上号码相对应的10名学生的考试情况就构成一个容量为10的样本.
(2)用随机数法抽取50名理科学生：
①将300名学生进行编号：001，002，003，\( \cdot \cdot \cdot \)299，300；
②利用随机数工具产生001\( \sim \)300范围内的整数随机数；
③把产生的随机数作为抽中的编号，使与编号对应的学生进入样本，直到抽足样本所需的50人。