
“微信扫一扫”进入题库练习及模拟考试
高中数学 必修 第二册(415题)
如图,在三棱台
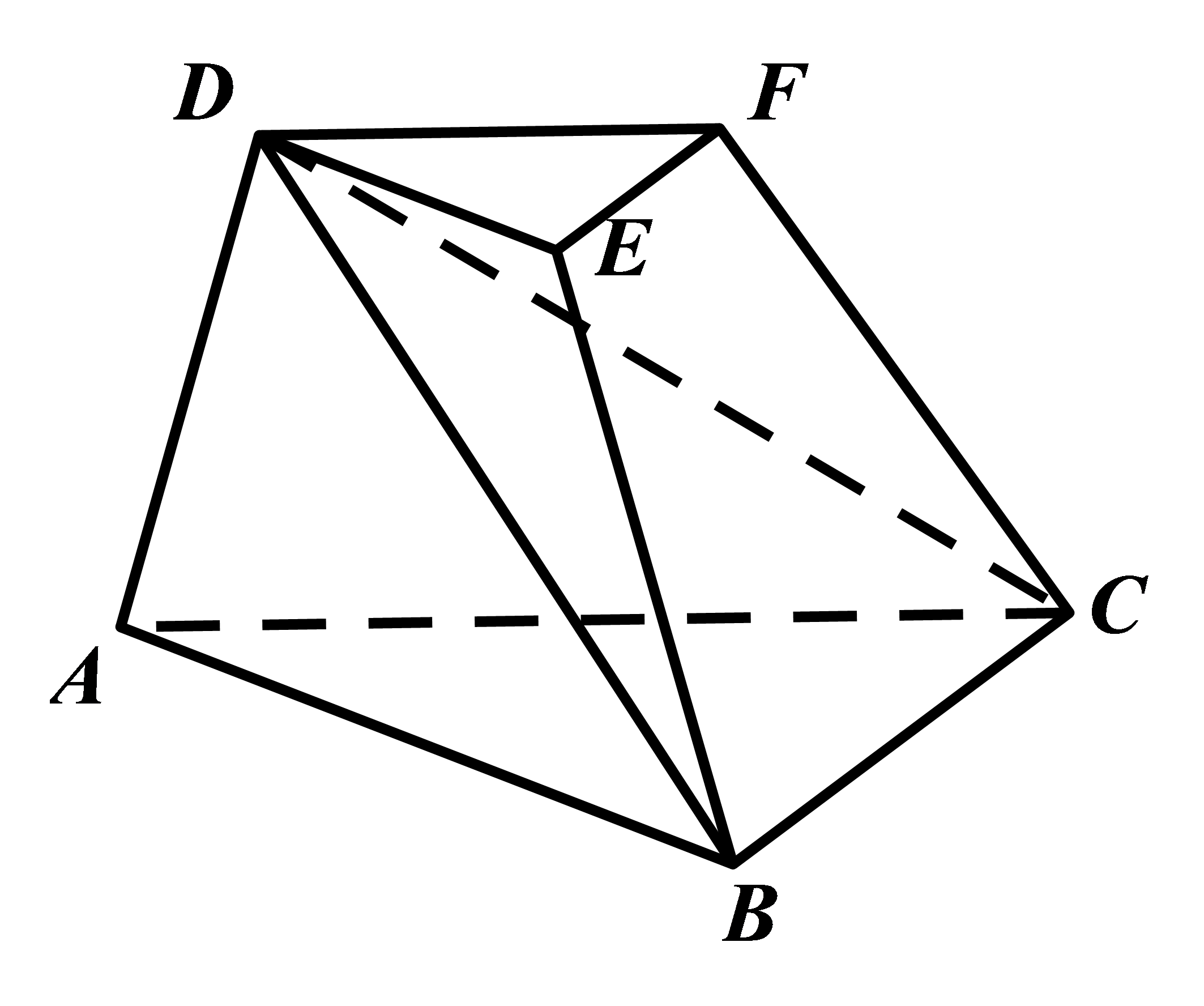
证明:
知识点:第八章 立体几何初步
参考答案:证明:设\(AD = \sqrt 2 a\),则\(AC = 2a\),
\(\because \angle ACD = 45^\circ \),
在\(\Delta ACD\)中,由余弦定理知,\(A{D^2} = A{C^2} + C{D^2} - 2AC \cdot CD\cos \angle ACD\),
\(\therefore 2{a^2} = 4{a^2} + C{D^2} - 2 \cdot 2a \cdot CD \cdot \frac{{\sqrt 2 }}{2}\),解得\(CD = \sqrt 2 a\),
\(\therefore A{D^2} + C{D^2} = A{C^2}\),即\(AD\bot CD\),
又平面\(ACFD\bot 平面DBC\),平面\(ACFD∩平面DBC=CD\),\(AD\subset 平面ACFD,\)
∴\(AD⊥\)平面\(DBC\),
\(\because BC \subset \)平面\(DBC\),
\(\therefore AD \bot BC\);