
“微信扫一扫”进入题库练习及模拟考试
高中数学 必修 第二册(415题)
如图,在矩形
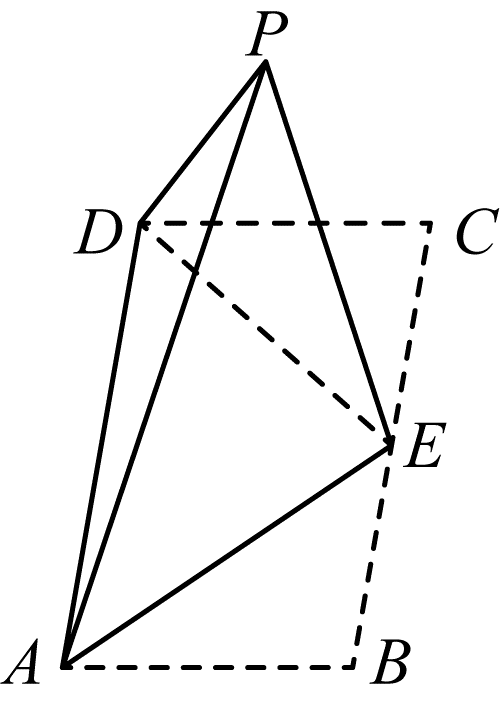
求证:平面
知识点:第八章 立体几何初步
参考答案:证明:由题意,\(AB \bot BE\),得\(AP \bot PE\),同理,\(DP \bot PE\)。
又因为\(AP \cap DP = P\),
所以\(PE \bot \)平面\(PAD\)。
又因为\(PE \subset \)平面\(PDE\),
所以平面\(PDE \bot \)平面\(PAD\)。