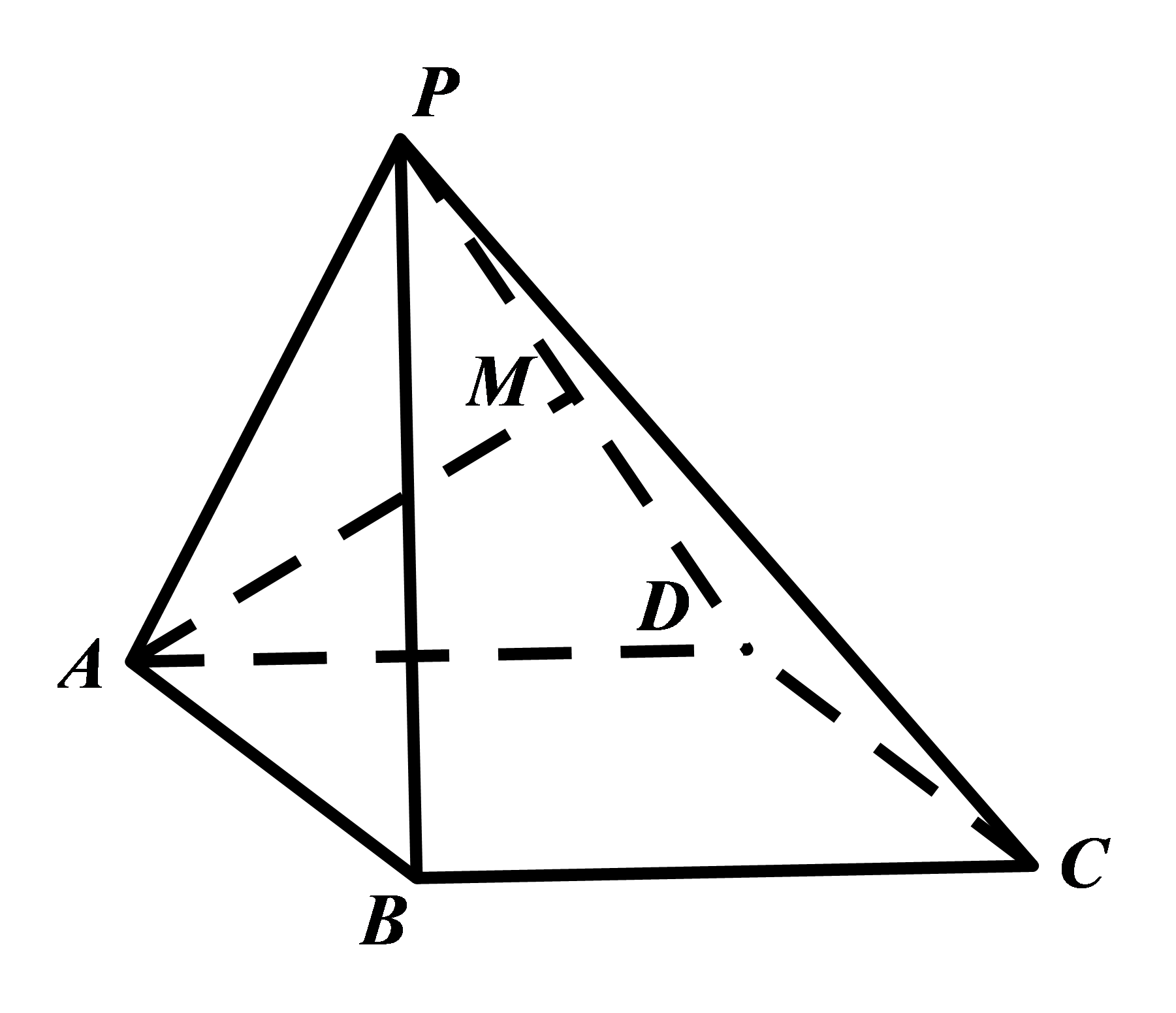
求侧面PBC与底面ABCD所成二面角的余弦值。

取AD的中点O，BC的中点N，

∵PO⊥AD，ON⊥AD，∴AD⊥平面PON，

又∵BC||AD，∴BC⊥平面PON，故BC⊥PN，

∵BC⊥PN，ON⊥BC，∴∠PNO是所求二面角的平面角．

设PA=a，∵△PAD为正三角形，底面ABCD为正方形，∴PO=\(\frac{{\sqrt 3 }}{2}a\)，ON=a．

∵PO⊥AD，侧面PAD⊥底面ABCD，∴PO⊥底面ABCD，PO⊥ON．

在Rt△PON中，\(P{N^2} = P{O^2} + O{N^2}\)，∴\(PN = \frac{{\sqrt 7 }}{2}a\)．

∴\(\cos \angle PNO = \frac{{ON}}{{PN}} = \frac{a}{{\frac{{\sqrt 7 }}{2}a}} = \frac{{2\sqrt 7 }}{7}\)

故侧面PBC与底面ABCD所成二面角的余弦值为\(\frac{{2\sqrt 7 }}{7}\)．

进入考试题库