
“微信扫一扫”进入题库练习及模拟考试
高中数学 必修 第二册(415题)
如图,在三棱台
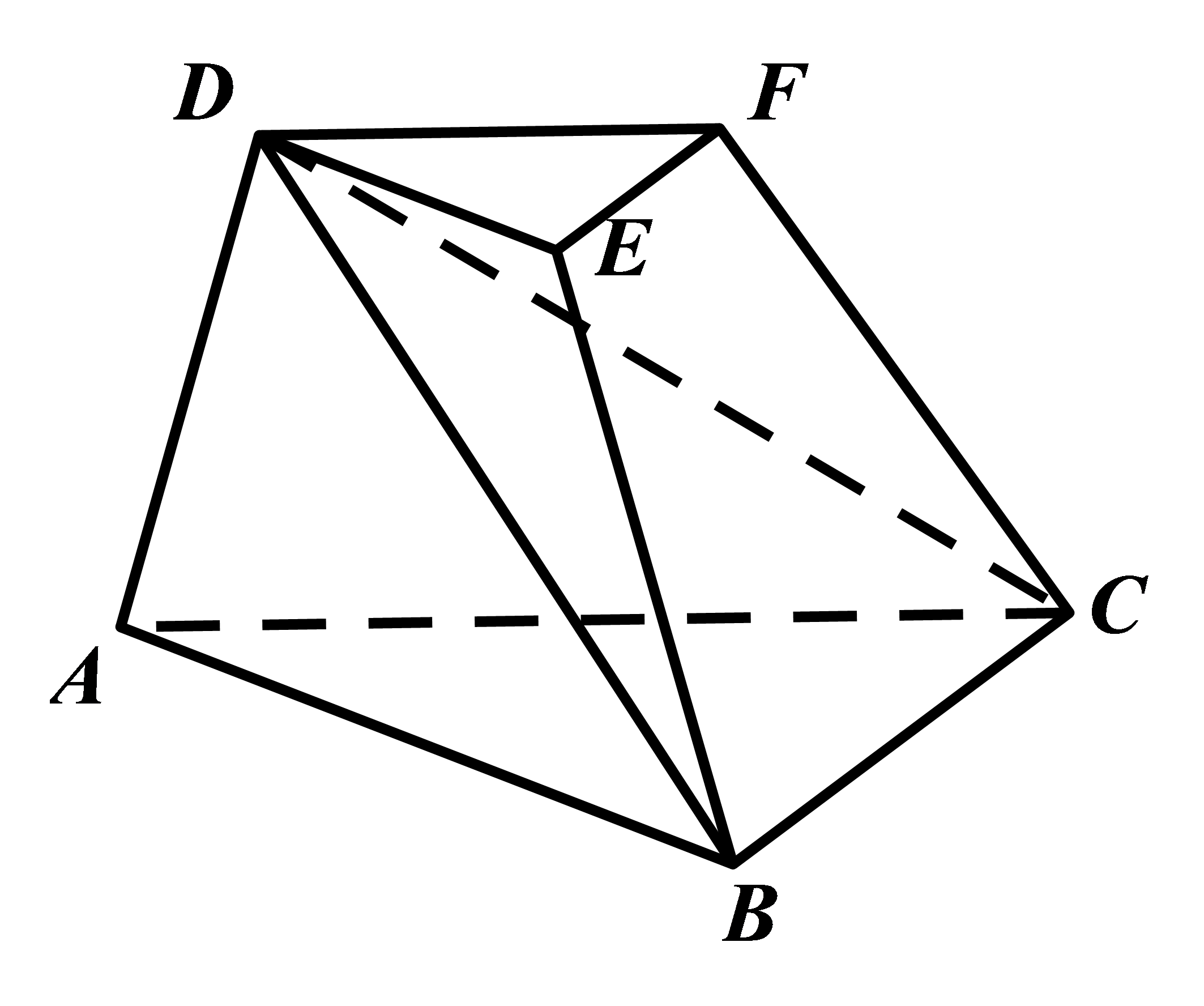
若
知识点:第八章 立体几何初步
参考答案:解:由三棱台的性质知,\(DE\)||\(AB\),
故直线\(DE\)与平面\(DBC\)所成角即为直线\(AB\)与平面\(DBC\)所成角.
由(1)知,\(AD \bot \)平面\(DBC\),
\(\therefore \angle ABD\)即为所求.
\(\because AD = \sqrt 2 BC\),\(AD = \sqrt 2 a\),\(\therefore BC = a\),
在\(\Delta ABC\)中,由余弦定理知,\(A{B^2} = A{C^2} + B{C^2} - 2AC\bullet BC\cos \angle ACB = 4{a^2} + {a^2} - 2\bullet 2a\bullet a\bullet \frac{1}{2} = 3{a^2}\),\(\therefore AB = \sqrt 3 a\),
在\({\rm{Rt}}\Delta {\rm{ABD}}\)中,\(\sin \angle ABD = \frac{{AD}}{{AB}} = \frac{{\sqrt 2 a}}{{\sqrt 3 a}} = \frac{{\sqrt 6 }}{3}\).
故直线\(DE\)与平面\(DBC\)所成角的正弦值为\(\frac{{\sqrt 6 }}{3}\).
`