第81题

将抛物线y=x²﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（　　）

A.y=（x﹣1）²+4

B.y=（x﹣4）²+4

C.y=（x+2）²+6

D.y=（x﹣4）²+6

参考答案：B

解析：

【考点】二次函数图象与几何变换．

【分析】根据函数图象向上平移加，向右平移减，可得函数解析式．

【解答】解：将y=x²﹣2x+3化为顶点式，得y=（x﹣1）²+2．

将抛物线y=x²﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为y=（x﹣4）²+4，

故选：B．

【点评】本题考查了二次函数图象与几何变换，函数图象的平移规律是：左加右减，上加下减．

第82题

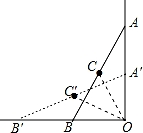
如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（　　）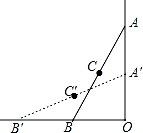

A.直线的一部分

B.圆的一部分

C.双曲线的一部分

D.抛物线的一部分

参考答案：B

解析：

【考点】轨迹；直角三角形斜边上的中线．

【分析】根据直角三角形斜边上的中线等于斜边的一半得到OC=AB=A′B′=OC′，从而得出滑动杆的中点C所经过的路径是一段圆弧．

【解答】解：连接OC、OC′，如图，

∵∠AOB=90°，C为AB中点，

∴OC=AB=A′B′=OC′，

∴当端点A沿直线AO向下滑动时，AB的中点C到O的距离始终为定长，

∴滑动杆的中点C所经过的路径是一段圆弧．

故选B．

【点评】本题考查了轨迹，圆的定义与性质，掌握直角三角形斜边上的中线等于斜边的一半是解题的关键．

第83题

如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（　　）

A.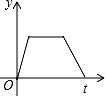

B.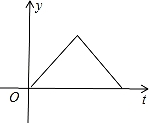

C.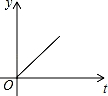

D.

参考答案：B

解析：

【考点】动点问题的函数图象．

【专题】数形结合．

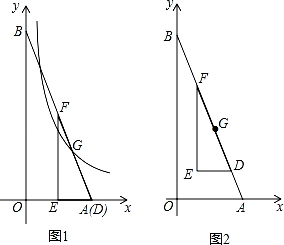
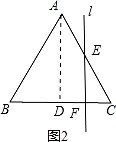
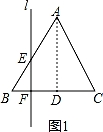
【分析】作AD⊥BC于D，如图，设点F运动的速度为1，BD=m，根据等腰三角形的性质得∠B=∠C，BD=CD=m，当点F从点B运动到D时，如图1，利用正切定义即可得到y=tanB•t（0≤t≤m）；当点F从点D运动到C时，如图2，利用正切定义可得y=tanC•CF=﹣tanB•t+2mtanB（m≤t≤2m），即y与t的函数关系为两个一次函数关系式，于是可对四个选项进行判断．

【解答】解：作AD⊥BC于D，如图，设点F运动的速度为1，BD=m，

∵△ABC为等腰三角形，

∴∠B=∠C，BD=CD，

当点F从点B运动到D时，如图1，

在Rt△BEF中，∵tanB=，

∴y=tanB•t（0≤t≤m）；

当点F从点D运动到C时，如图2，

在Rt△CEF中，∵tanC=，

∴y=tanC•CF

=tanC•（2m﹣t）

=﹣tanB•t+2mtanB（m≤t≤2m）．

故选B．

【点评】本题考查了动点问题的函数图象：利用三角函数关系得到两变量的函数关系，再利用函数关系式画出对应的函数图象．注意自变量的取值范围．

第84题

如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得扇形DAB的面积为（　　）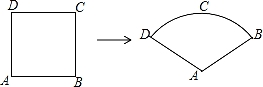

A.6

B.7

C.8

D.9

参考答案：D

解析：

【考点】扇形面积的计算．

【分析】由正方形的边长为3，可得弧BD的弧长为6，然后利用扇形的面积公式：S_扇形DAB=，计算即可．

【解答】解：∵正方形的边长为3，

∴弧BD的弧长=6，

∴S_扇形DAB==×6×3=9．

故选D．

【点评】此题考查了扇形的面积公式，解题的关键是：熟记扇形的面积公式S_扇形DAB=．

第85题

多项式a²﹣4因式分解的结果是　　．

参考答案：（a+2）（a﹣2）

解析：

【考点】因式分解-运用公式法．

【分析】直接利用平方差公式分解因式得出即可．

【解答】解：a²﹣4=（a+2）（a﹣2）．

故答案为：（a+2）（a﹣2）．

【点评】此题主要考查了公式法分解因式，熟练应用平方差公式是解题关键．

第86题

使式子1+有意义的x的取值范围是　　．

参考答案：x≥0

解析：

【考点】二次根式有意义的条件．

【分析】根据被开方数大于等于0列式即可．

【解答】解：由题意得，x≥0．

故答案为：x≥0．

【点评】本题考查的知识点为：二次根式的被开方数是非负数．

第87题

2014年南京青奥会某项目6名礼仪小姐的身高如下（单位：cm）：168，166，168，167，169，168，则她们身高的众数是　　cm．

参考答案：168

解析：

【考点】众数．

【分析】根据众数的定义找出这组数据中出现次数最多的数即可得出答案．

【解答】解：168出现了3次，出现的次数最多，则她们身高的众数是168cm；

故答案为：168；

【点评】此题考查了众数众数是一组数据中出现次数最多的数，属于基础题，难度不大．

第88题

化简： =　　．

参考答案：

解析：

【考点】分式的加减法．

【专题】计算题；压轴题．

【分析】先将x²﹣4分解为（x+2）（x﹣2），然后通分，再进行计算．

【解答】解： ===．

【点评】本题考查了分式的计算和化简．解决这类题关键是把握好通分与约分．分式加减的本质是通分，乘除的本质是约分．

第89题

已知如图所示的图形的面积为24，根据图中的条件，可列出方程：　　．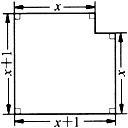

参考答案：（x+1）^2=25

解析：

【考点】由实际问题抽象出一元二次方程．

【专题】几何图形问题．

【分析】此图形的面积等于两个正方形的面积的差，据此可以列出方程．

【解答】解：根据题意得：（x+1）²﹣1=24，

即：（x+1）²=25．

故答案为：（x+1）²=25．

【点评】本题考查了由实际问题抽象出一元二次方程，解题的关键是明确题目中的不规则图形的面积计算方法．

第90题

取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．最少经过下面5步运算可得1，即：5168421，如果自然数m最少经过7步运算可得到1，则所有符合条件的m的最小值为　　．

参考答案：3

解析：

【考点】规律型：数字的变化类．

【分析】利用列举法，尝试最小的几个非0自然数，再结合“自然数5．最少经过5步运算可得1”，即可得出结论．

【解答】解：利用列举法进行尝试，

1（不用运算）；

21（1步运算）；

3105，结合已知给定案例可知，5再经过5步运算可得1，

故3要经过7步运算可得1．

故答案为：3．

【点评】本题考查了数字的变换类，解题的关键是：利用列举法，尝试几个最小的非0自然数．

第91题

计算：﹣2³÷|﹣2|×cos45°．

参考答案：见解析

解析：

【考点】实数的运算；特殊角的三角函数值．

【专题】计算题；实数．

【分析】原式第一项利用算术平方根定义计算，第二项利用乘方的意义，绝对值的代数意义，以及特殊角的三角函数值计算即可得到结果．

【解答】解：原式=2﹣8÷2×=2﹣2．

【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

第92题

解不等式，并把解在数轴上表示出来．

参考答案：见解析

解析：

【考点】解一元一次不等式；不等式的性质；在数轴上表示不等式的解集．

【专题】计算题；数形结合．

【分析】根据不等式的性质得到3（x﹣1）≤1+x，推出2x≤4，即可求出不等式的解集．

【解答】解：去分母，得3（x﹣1）≤1+x，

整理，得2x≤4，

∴x≤2．

在数轴上表示为：．

【点评】本题主要考查对解一元一次不等式，在数轴上表示不等式的解集，不等式的性质等知识点的理解和掌握，能根据不等式的性质正确解不等式是解此题的关键．

第93题

研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？

操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，放回盒中，再继续．

参考答案：见解析

解析：

【考点】模拟实验；利用频率估计概率．

【专题】应用题；压轴题．

【分析】（1）根据表格数据可以得到50次摸球实验活动中，出现红球20次，黄球30次，由此即可求出盒中红球、黄球各占总球数的百分比；

（2）由题意可知50次摸球实验活动中，出现有记号的球4次，由此可以求出总球数，然后利用（1）的结论即可求出盒中红球．

【解答】解：（1）由题意可知，50次摸球实验活动中，出现红球20次，黄球30次，

∴红球所占百分比为20÷50=40%，

黄球所占百分比为30÷50=60%，

答：红球占40%，黄球占60%；

（2）由题意可知，50次摸球实验活动中，出现有记号的球4次，

∴总球数为8÷=100，

∴红球数为100×40%=40，

答：盒中红球有40个．

【点评】此题主要考查了利用频率估计概率的问题，首先利用模拟实验得到盒中红球、黄球各占总球数的百分比，然后利用百分比即可求出盒中红球个数．

第94题

如图，⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D．

（1）求的长．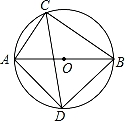

参考答案：见解析

解析：

【考点】圆周角定理；含30度角的直角三角形；等腰直角三角形；弧长的计算．

【分析】（1）首先根据AB是⊙O的直径，可得∠ACB=∠ADB=90°，然后在Rt△ABC中，求出∠BAC的度数，即可求出∠BOC的度数；最后根据弧长公式，求出的长即可．

（2）首先根据CD平分∠ACB，可得∠ACD=∠BCD；然后根据圆周角定理，可得∠AOD=∠BOD，所以AD=BD，∠ABD=∠BAD=45°；最后在Rt△ABD中，求出弦BD的长是多少即可．

【解答】解：（1）如图，连接OC，OD，，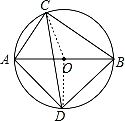

∵AB是⊙O的直径，

∴∠ACB=∠ADB=90°，

在Rt△ABC中，

∵，

∴∠BAC=60°，

∴∠BOC=2∠BAC=2×60°=120°，

∴的长=．

（2）∵CD平分∠ACB，

∴∠ACD=∠BCD，

∴∠AOD=∠BOD，

∴AD=BD，

∴∠ABD=∠BAD=45°，

在Rt△ABD中，

BD=AB×sin45°=10×．

【点评】（1）此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，要熟练掌握．

（2）此题还考查了含30度角的直角三角形，以及等腰直角三角形的性质和应用，要熟练掌握．

（3）此题还考查了弧长的求法，要熟练掌握，解答此题的关键是要明确：①弧长公式：l=（弧长为l，圆心角度数为n，圆的半径为R）．②在弧长的计算公式中，n是表示1°的圆心角的倍数，n和180都不要带单位．

第95题

某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．

（1）该商家购进的第一批衬衫是多少件？

参考答案：见解析

解析：

【考点】分式方程的应用；一元一次不等式的应用．

【分析】（1）可设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，根据第二批这种衬衫单价贵了10元，列出方程求解即可；

（2）设每件衬衫的标价y元，求出利润表达式，然后列不等式解答．

【解答】解：（1）设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，依题意有

+10=，

解得x=120，

经检验，x=120是原方程的解，且符合题意．

答：该商家购进的第一批衬衫是120件．

（2）3x=3×120=360，

设每件衬衫的标价y元，依题意有

（360﹣50）y+50×0.8y≥（13200+28800）×（1+25%），

解得y≥150．

答：每件衬衫的标价至少是150元．

【点评】本题考查了分式方程的应用和一元一次不等式的应用，弄清题意并找出题中的数量关系并列出方程是解题的关键．

第96题

如图，已知点A（4，0），B（0，4），把一个直角三角尺DEF放在△OAB内，使其斜边FD在线段AB上，三角尺可沿着线段AB上下滑动．其中∠EFD=30°，ED=2，点G为边FD的中点．

（1）求直线AB的解析式；

参考答案：见解析

解析：

【考点】反比例函数综合题．

【分析】（1）设直线AB的解析式为y=kx+b，把点A、B的坐标代入，组成方程组，解方程组求出k、b的值即可；

（2）由Rt△DEF中，求出EF、DF，在求出点D坐标，得出点F、G坐标，把点G坐标代入反比例函数求出k即可；

（3）设F（t，﹣t+4），得出D、G坐标，设过点G和F的反比例函数解析式为y=，用待定系数法求出t、m，即可得出反比例函数解析式．

【解答】解：（1）设直线AB的解析式为y=kx+b，

∵A（4，0），B（0，4），

∴，

解得：，

∴直线AB的解析式为：y=﹣x+4；

（2）∵在Rt△DEF中，∠EFD=30°，ED=2，

∴EF=2，DF=4，

∵点D与点A重合，

∴D（4，0），

∴F（2，2），

∴G（3，），

∵反比例函数y=经过点G，

∴k=3，

∴反比例函数的解析式为：y=；

（3）经过点G的反比例函数的图象能同时经过点F；理由如下：

∵点F在直线AB上，

∴设F（t，﹣t+4），

又∵ED=2，

∴D（t+2，﹣t+2），

∵点G为边FD的中点．

∴G（t+1，﹣t+3），

若过点G的反比例函数的图象也经过点F，

设解析式为y=，

则，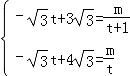

整理得：（﹣t+3）（t+1）=（﹣t+4）t，

解得：t=，

∴m=，

∴经过点G的反比例函数的图象能同时经过点F，这个反比例函数解析式为：y=．

【点评】本题是反比例函数综合题目，考查了用待定系数法求一次函数的解析式、求反比例函数的解析式、坐标与图形特征、解直角三角形、解方程组等知识；本题难度较大，综合性强，用待定系数法确定一次函数和反比例函数的解析式是解决问题的关键．

第97题

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D、E分别是边BC、AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．

参考答案：见解析

解析：

【考点】几何变换综合题．

【专题】压轴题．

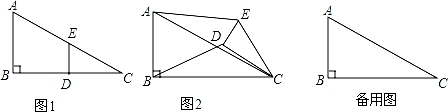
【分析】（1）①当α=0°时，在Rt△ABC中，由勾股定理，求出AC的值是多少；然后根据点D、E分别是边BC、AC的中点，分别求出AE、BD的大小，即可求出的值是多少．

②α=180°时，可得AB∥DE，然后根据，求出的值是多少即可．

（2）首先判断出∠ECA=∠DCB，再根据，判断出△ECA∽△DCB，即可求出的值是多少，进而判断出的大小没有变化即可．

（3）根据题意，分两种情况：①点A，D，E所在的直线和BC平行时；②点A，D，E所在的直线和BC相交时；然后分类讨论，求出线段BD的长各是多少即可．

【解答】解：（1）①当α=0°时，

∵Rt△ABC中，∠B=90°，

∴AC=，

∵点D、E分别是边BC、AC的中点，

∴，

∴．

②如图1，，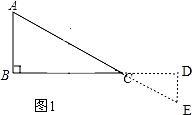

当α=180°时，

可得AB∥DE，

∵，

∴=．

故答案为：．

（2）如图2，，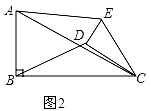

当0°≤α＜360°时，的大小没有变化，

∵∠ECD=∠ACB，

∴∠ECA=∠DCB，

又∵，

∴△ECA∽△DCB，

∴．

（3）①如图3，，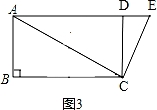

∵AC=4，CD=4，CD⊥AD，

∴AD==，

∵AD=BC，AB=DC，∠B=90°，

∴四边形ABCD是矩形，

∴．

②如图4，连接BD，过点D作AC的垂线交AC于点Q，过点B作AC的垂线交AC于点P，

，

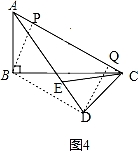∵AC=4，CD=4，CD⊥AD，

∴AD==，

∵点D、E分别是边BC、AC的中点，

∴DE==2，

∴AE=AD﹣DE=8﹣2=6，

由（2），可得

，

∴BD==．

综上所述，BD的长为4或．

【点评】（1）此题主要考查了几何变换综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，要熟练掌握．

（2）此题还考查了相似三角形、全等三角形的判定和性质的应用，要熟练掌握．

（3）此题还考查了线段长度的求法，以及矩形的判定和性质的应用，要熟练掌握．

第98题

如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

参考答案：见解析

解析：

【考点】二次函数综合题．

【专题】压轴题．

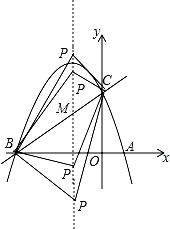
【分析】（1）先把点A，C的坐标分别代入抛物线解析式得到a和b，c的关系式，再根据抛物线的对称轴方程可得a和b的关系，再联立得到方程组，解方程组，求出a，b，c的值即可得到抛物线解析式；把B、C两点的坐标代入直线y=mx+n，解方程组求出m和n的值即可得到直线解析式；

（2）设直线BC与对称轴x=﹣1的交点为M，则此时MA+MC的值最小．把x=﹣1代入直线y=x+3得y的值，即可求出点M坐标；

（3）设P（﹣1，t），又因为B（﹣3，0），C（0，3），所以可得BC²=18，PB²=（﹣1+3）²+t²=4+t²，PC²=（﹣1）²+（t﹣3）²=t²﹣6t+10，再分三种情况分别讨论求出符合题意t值即可求出点P的坐标．

【解答】解：（1）依题意得：，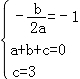

解之得：，

∴抛物线解析式为y=﹣x²﹣2x+3

∵对称轴为x=﹣1，且抛物线经过A（1，0），

∴把B（﹣3，0）、C（0，3）分别代入直线y=mx+n，

得，

解之得：，

∴直线y=mx+n的解析式为y=x+3；

（2）设直线BC与对称轴x=﹣1的交点为M，则此时MA+MC的值最小．

把x=﹣1代入直线y=x+3得，y=2，

∴M（﹣1，2），

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（﹣1，2）；

（3）设P（﹣1，t），

又∵B（﹣3，0），C（0，3），

∴BC²=18，PB²=（﹣1+3）²+t²=4+t²，PC²=（﹣1）²+（t﹣3）²=t²﹣6t+10，

①若点B为直角顶点，则BC²+PB²=PC²即：18+4+t²=t²﹣6t+10解之得：t=﹣2；

②若点C为直角顶点，则BC²+PC²=PB²即：18+t²﹣6t+10=4+t²解之得：t=4，

③若点P为直角顶点，则PB²+PC²=BC²即：4+t²+t²﹣6t+10=18解之得：t₁=，t₂=；

综上所述P的坐标为（﹣1，﹣2）或（﹣1，4）或（﹣1，） 或（﹣1，）．

【点评】本题综合考查了二次函数的图象与性质、待定系数法求函数（二次函数和一次函数）的解析式、利用轴对称性质确定线段的最小长度、难度不是很大，是一道不错的中考压轴题．

第99题

在﹣2，0，2，﹣3这四个数中，最小的数是（　　）

A.2

B.0

C.﹣2

D.﹣3

参考答案：D

解析：

【考点】有理数大小比较．

【专题】计算题．

【分析】根据有理数的大小比较法则（正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小比较即可．

【解答】解：∵﹣3＜﹣2＜0＜2，

∴最小的数是﹣3，

故选D．

【点评】本题考查了有理数的大小比较法则，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．

第100题

一元二次方程（x+6）²=16可转化为两个一元一次方程，其中一个一元一次方程是x+6=4，则另一个一元一次方程是（　　）

A.x﹣6=﹣4

B.x﹣6=4

C.x+6=4

D.x+6=﹣4

参考答案：D

解析：

【考点】解一元二次方程-直接开平方法．

【分析】方程两边直接开平方可达到降次的目的，进而可直接得到答案．

【解答】解：（x+6）²=16，

两边直接开平方得：x+6=±4，

则：x+6=4，x+6=﹣4，

故选：D．

【点评】本题主要考查了直接开平方法解一元二次方程，关键是将方程右侧看做一个非负已知数，根据法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”来求解．