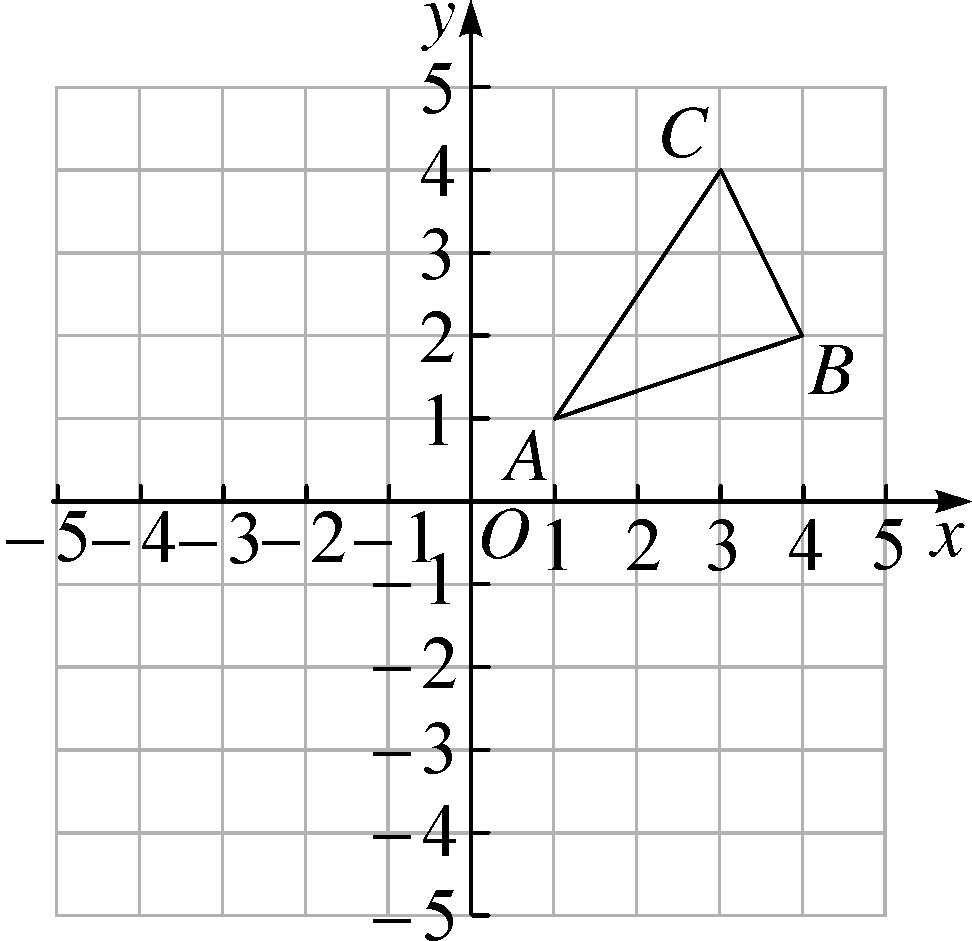第321题

如图，在平面直角坐标系中，已知点A(1，0)，B(1－a，0)，C(1＋a，0)(a＞0)，点P在以D(4，4)为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则a的最大值是______.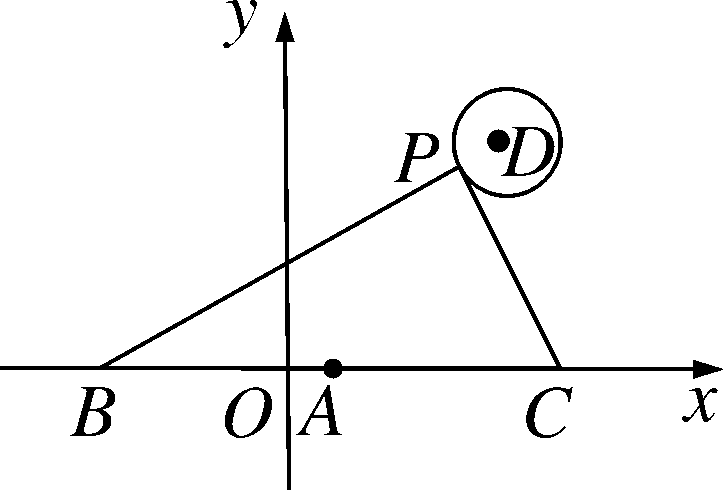

参考答案：6

解析：

解析：∵A（1，0），B（1－a，0），C（1＋a，0）（a＞0），∴AB＝1－（1－a）＝a，CA＝a＋1－1＝a，∴AB＝AC.∵∠BPC＝90°，∴PA＝AB＝AC＝a.如图，延长AD交⊙D于P′，此时AP′最大.∵A（1，0），D（4，4），∴AD＝5，∴AP′＝5＋1＝6，∴a的最大值为6.

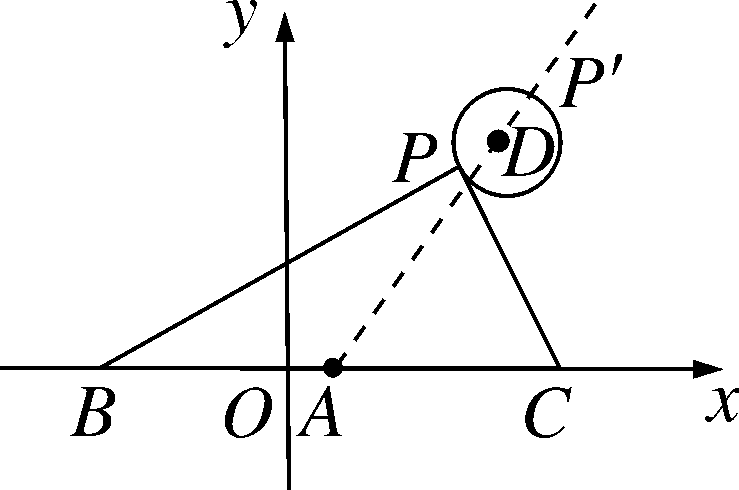
第322题

(8分)用适当的方法解下列方程：

(1)3x(x＋3)＝2(x＋3);

参考答案：见解析

解析：

解：（1）x₁＝，x₂＝－3；（4分）

（2）x₁＝1＋，x₂＝1－.（8分）

第323题

(8分)已知抛物线y＝－x²＋bx＋c与直线y＝－4x＋m相交于第一象限内不同的两点A(5，n)，B(3，9)，求此抛物线的解析式．

参考答案：见解析

解析：

解：∵直线y＝－4x＋m过点B（3，9），∴9＝－4×3＋m，解得m＝21，∴直线的解析式为y＝－4x＋21.（2分）∵点A（5，n）在直线y＝－4x＋21上，∴n＝－4×5＋21＝1，

∴点A（5，1）.（4分）将点A（5，1），B（3，9）代入y＝－x²＋bx＋c中，

得)

∴此抛物线的解析式为y＝－x²＋4x＋6.（8分）

第324题

(8分)如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．

(1)请画出△ABC向左平移5个单位长度后得到的△A₁B₁C₁；

参考答案：见解析

解析：

解：（1）△A₁B₁C₁如图所示；（2分）

（2）△A₂B₂C₂如图所示；（4分）

（3）△PAB如图所示，P（2，0）.（8分）

第325题

(10分)在⊙O中，AB为直径，C为⊙O上一点．

(1)如图①，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB＝27°，求∠P的大小；

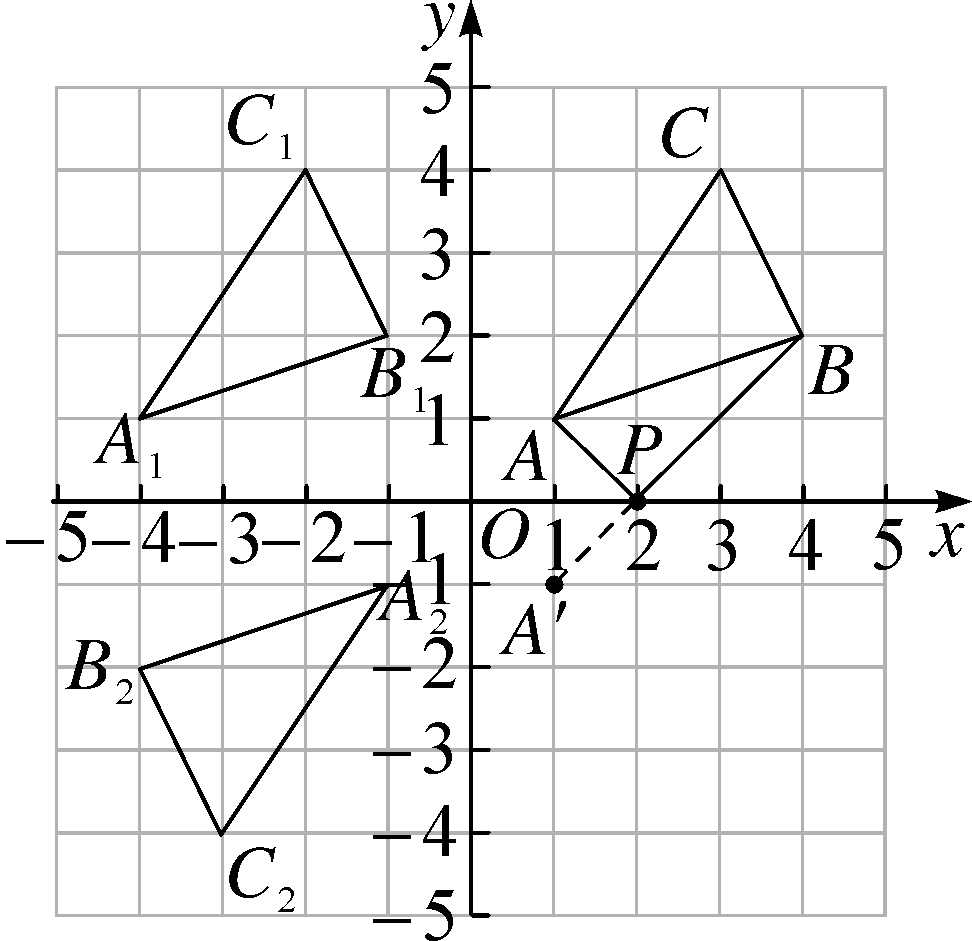
参考答案：见解析

解析：

解：（1）连接OC，∵⊙O与PC相切于点C，∴OC⊥PC，即∠OCP＝90°.（2分）∵OA＝OC，∴∠OCA＝∠CAB＝27°，∴∠COB＝2∠CAB＝54°.在Rt△COP中，∠P＋∠COP＝90°，∴∠P＝90°－∠COP＝36°；（5分）

（2）∵E为AC的中点，∴OD⊥AC，即∠AEO＝90°.（6分）在Rt△AOE中，由∠EAO＝10°，得∠AOE＝90°－∠EAO＝80°，∴∠ACD＝∠AOD＝40°.（8分）∵∠ACD是△ACP的一个外角，∴∠P＝∠ACD－∠A＝40°－10°＝30°.（10分）

第326题

(10分)某中学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放(发放的食品价格一样)，食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．

(1)按约定，“小李同学在该天早餐得到两个油饼”是_______事件(填“可能”“必然”或“不可能”)；

参考答案：见解析

解析：

解：（1）不可能（4分）

（2）画树状图如下：（8分）

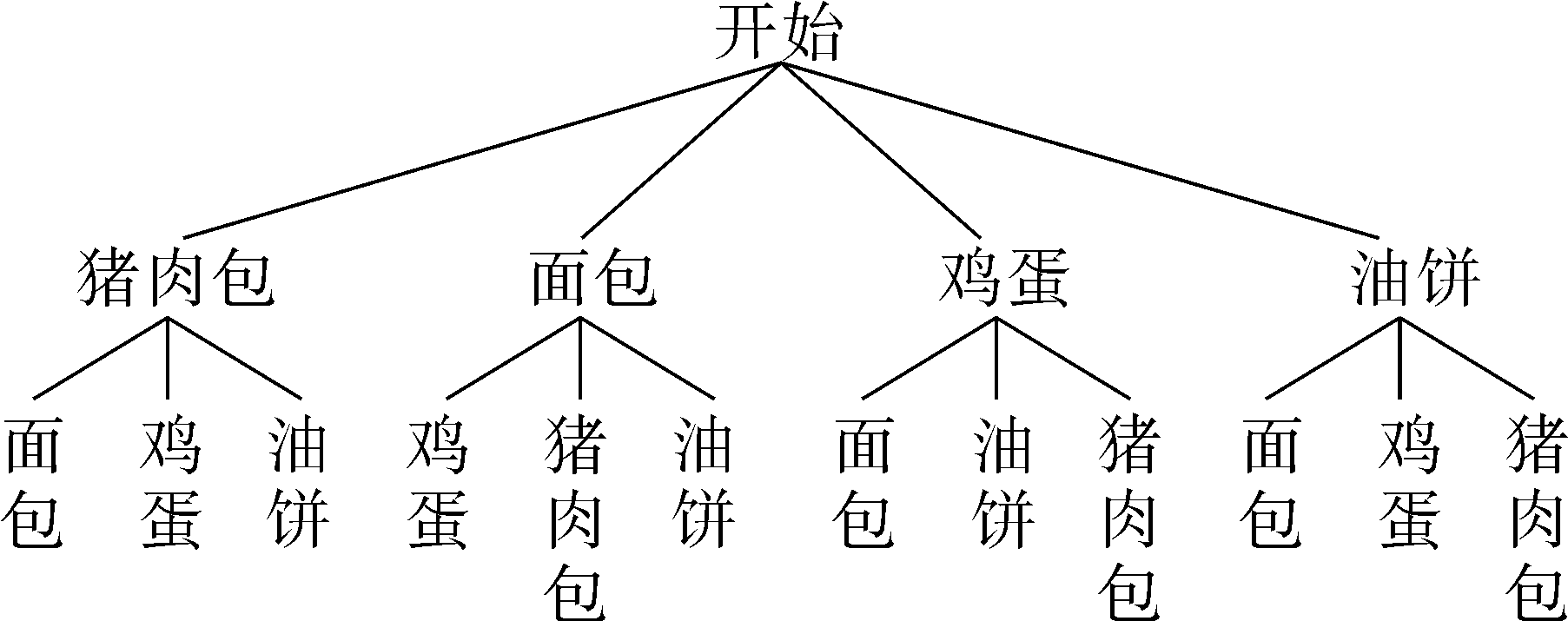
共有12种等可能的结果，刚好得到猪肉包和油饼的有2种情况，∴小张同学得到猪肉包和油饼的概率为12(2)＝6(1).（10分）

第327题

(10分)如图，在四边形ABCD中，AD∥BC，AD＝2，AB＝2√2，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F.

(1)求∠ABE的大小及DEF(︵)的长度；

参考答案：见解析

解析：

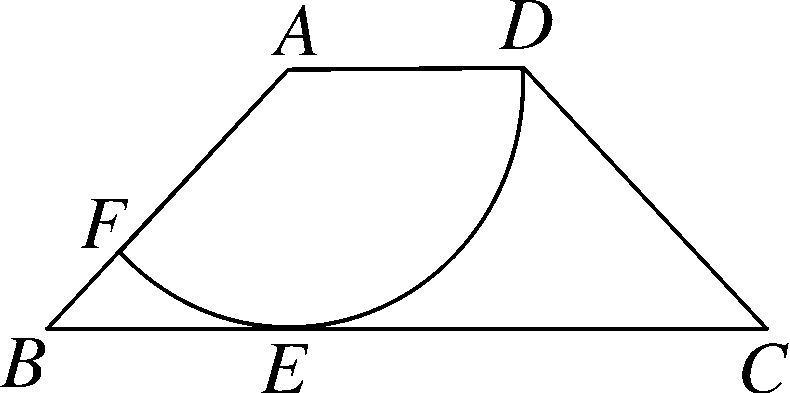
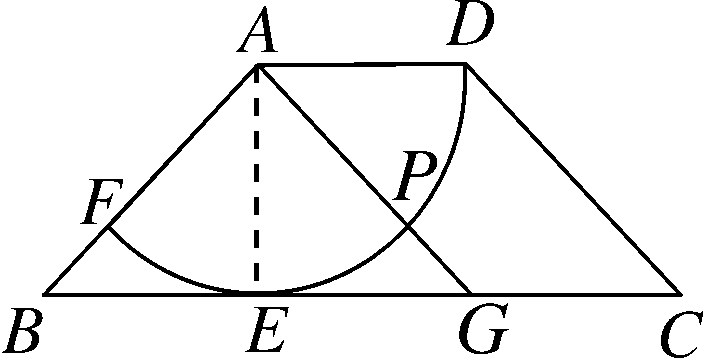
解：（1）连接AE，如图，∵以AD为半径的圆与BC相切于点E，∴AE⊥BC，AE＝AD＝2.（1分）在Rt△AEB中，AE＝2，AB＝2√2，∴BE＝2，即△ABE是等腰直角三角形，∴∠ABE＝45°.（3分）∵AD∥BC，∴∠DAB＋∠ABE＝180°，∴∠DAB＝135°，∴DEF(︵)的长度为；（5分）

（2）如图，根据两点之间线段最短，可得当A，P，G三点共线时PG最短，（7分）此时AG＝AP＋PG＝2＋2√2－2＝2√2，∴AG＝AB.（9分）∵AE⊥BG，∴BE＝EG.∴BG＝2BE＝4.（10分）

第328题

(12分)如图，在平面直角坐标系中，抛物线y＝ax²＋bx＋c的顶点坐标为(2，9)，与y轴交于点A(0，5)，与x轴交于点E，B.

(1)求二次函数y＝ax²＋bx＋c的表达式；

参考答案：见解析

解析：

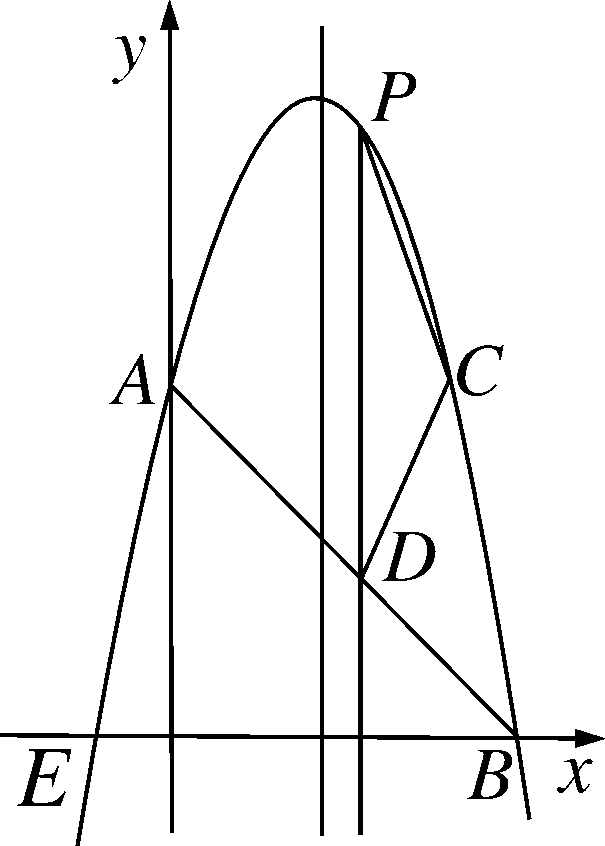
解：（1）设抛物线解析式为y＝a（x－2）²＋9，（1分）∵抛物线与y轴交于点A（0，5），∴4a＋9＝5，∴a＝－1，∴y＝－（x－2）²＋9＝－x²＋4x＋5；（3分）

（2）当y＝0时，－x²＋4x＋5＝0，∴x₁＝－1，x₂＝5，∴E（－1，0），B（5，0）.（4分）设直线AB的解析式为y＝mx＋n，∵A（0，5），B（5，0），∴m＝－1，n＝5，∴直线AB的解析式为y＝－x＋5.设P（x，－x²＋4x＋5），∴D（x，－x＋5），∴PD＝－x²＋4x＋5＋x－5＝－x²＋5x.（5分）∵AC∥x轴，∴点A，C关于对称轴对称，AC＝4.∵AC⊥PD，∴S_{四边形APCD}＝×AC×PD＝2（－x²＋5x）＝－2x²＋10x，

∴当时，即点P的坐标为时，S_{四边形APCD最大}＝；（7分）

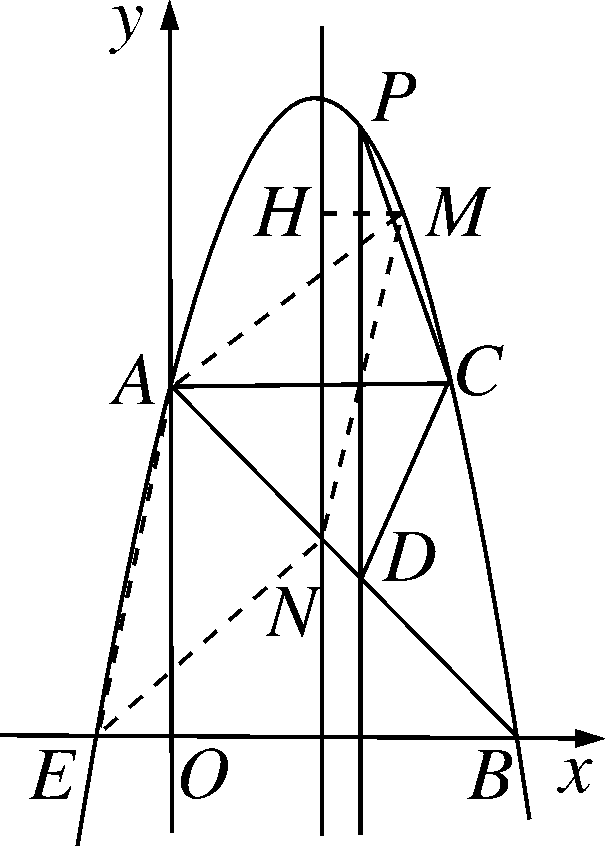
（3）如图，过M作MH垂直于对称轴，垂足为H.∵MN∥AE，MN＝AE，∴△HMN≌△OEA，∴HM＝OE＝1，∴M点的横坐标为3或1.当横坐标1时，M点纵坐标为8，当横坐标为3时，M点纵坐标为8，∴M点的坐标为M₁（1，8）或M₂（3，8）.（9分）∵A（0，5），E（－1，0），∴直线AE的解析式为y＝5x＋5.∵MN∥AE，∴MN的解析式为y＝5x＋b.∵点N在抛物线对称轴x＝2上，∴N（2，10＋b）.∵AE²＝OA²＋OE²＝26＝MN²，∴MN2＝（2－1）²＋[8－（10＋b）]²＝1＋（b＋2）².∵M点的坐标为M₁（1，8）或M₂（3，8），∴点M₁，M₂关于抛物线对称轴x＝2对称.∵点N在抛物线对称轴上，∴M₁N＝M₂N.∴1＋（b＋2）²＝26，∴b＝3或b＝－7，∴10＋b＝13或10＋b＝3.∴当M点的坐标为（1，8）时，N点坐标为（2，13），当M点的坐标为（3，8）时，N点坐标为（2，3）.（12分）