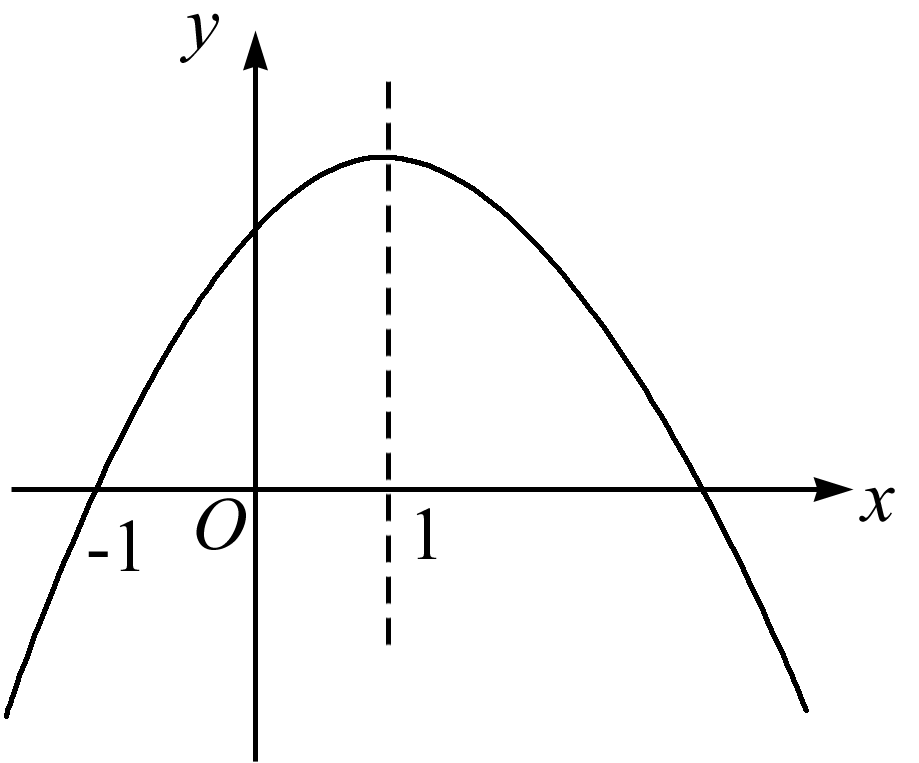第201题

学校实施新课程改革以来，学生的学习能力有了很大提高，王老师为进一步了解本班学生自主学习、合作交流的现状，对该班部分学生进行调查，把调查结果分成四类(A：特别好，B：好，C：一般，D：较差)后，再将调查结果绘制成两幅不完整的统计图(如图①②)．请根据统计图解答下列问题：

(1)本次调查中，王老师一共调查了________名学生；

参考答案：见解析

解析：

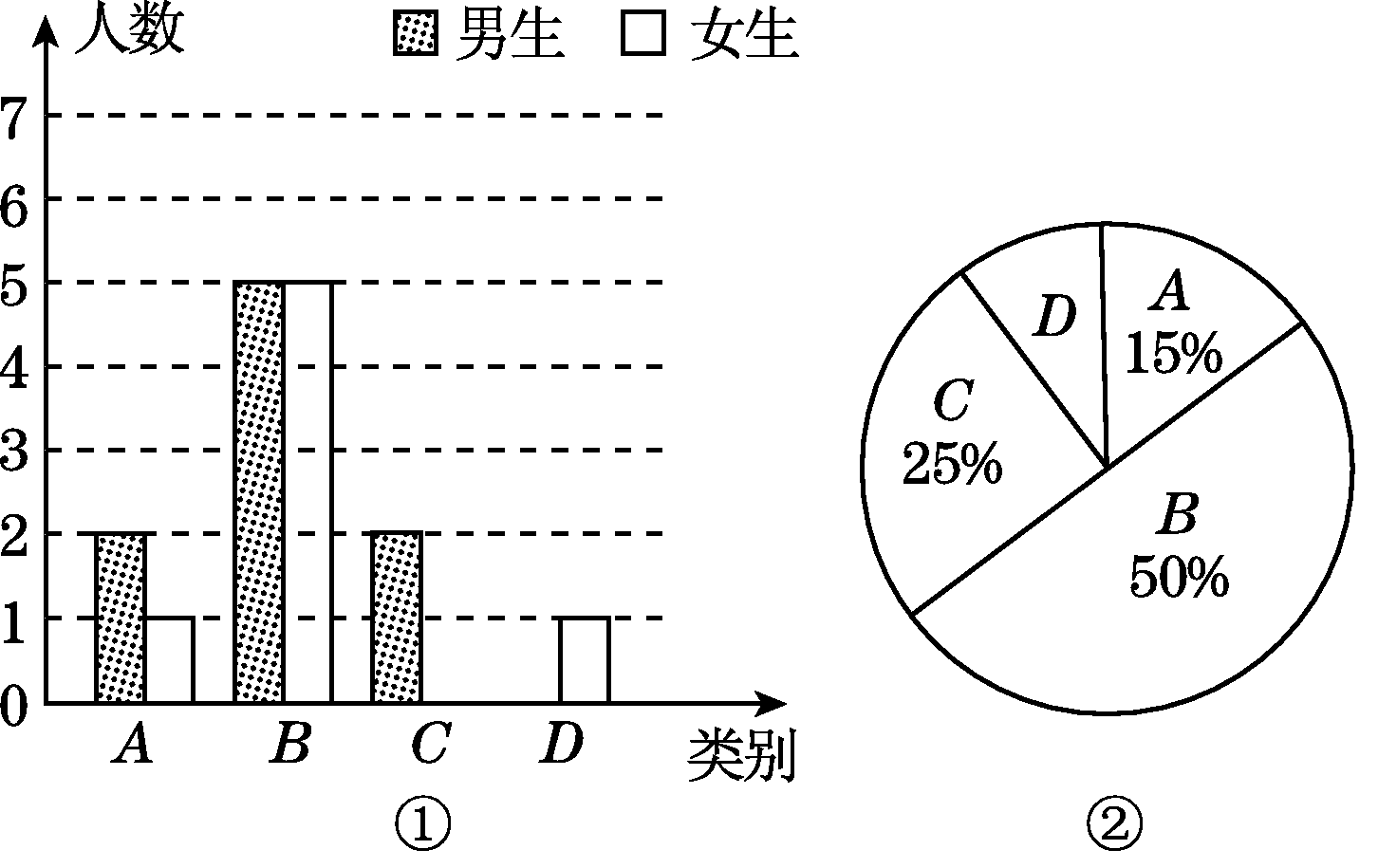
解：(1)20

(2)如图：

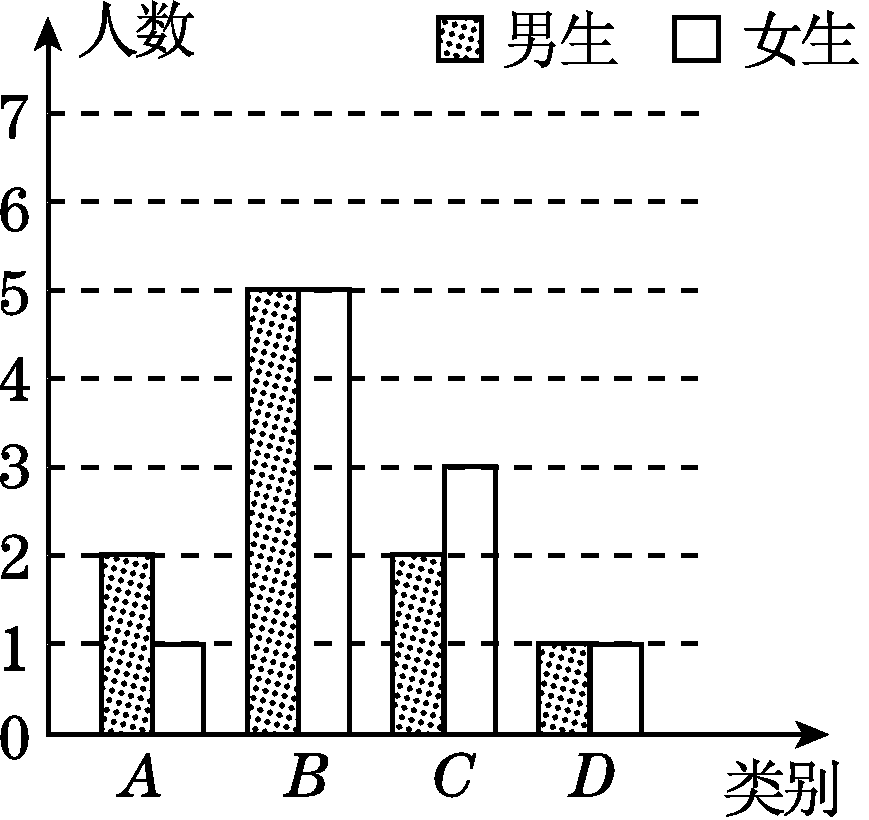
(3)列表如下，A类学生中的两名男生分别记为男A₁和男A₂，

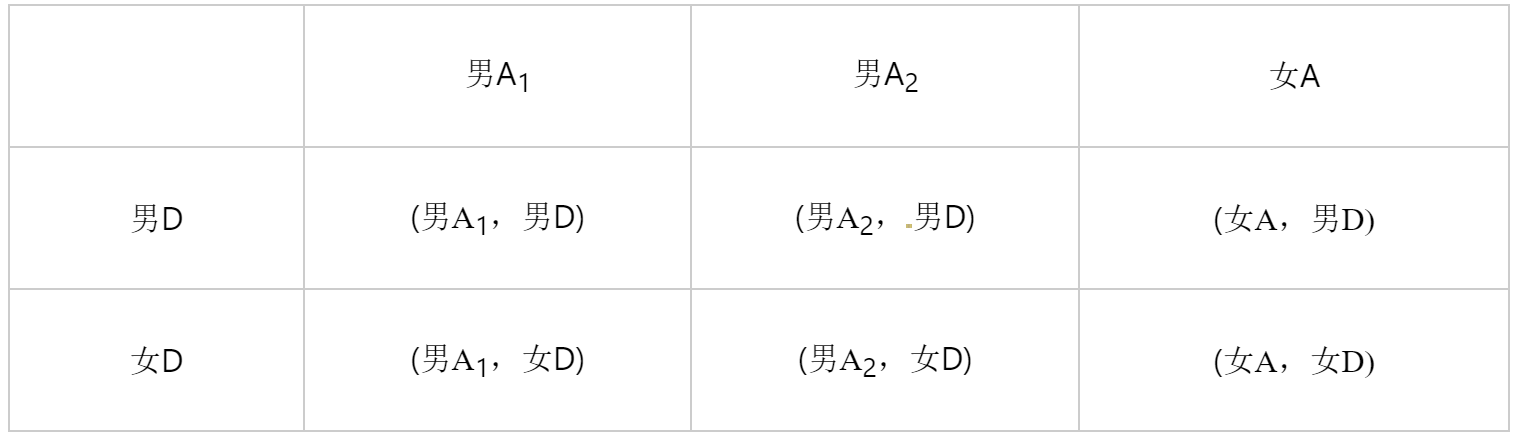
共有6种等可能的结果，其中，一男一女的有3种，所以所选两名学生恰好是一名男生和一名女生的概率为6(3)＝2(1).

第202题

某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．

(1)写出商场销售这种文具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；

参考答案：见解析

解析：

解：(1)由题意得，销售量为250－10(x－25)＝－10x＋500，

则w＝(x－20)(－10x＋500)＝－10x²＋700x－10 000.

(2)w＝－10x²＋700x－10 000＝－10(x－35)²＋2 250.

∵－10<0，∴函数图象开口向下，w有最大值．

当x＝35时，w_最大＝2 250.

故当销售单价为35元时，该文具每天的销售利润最大．

(3)A方案的最大利润更高，理由如下：

A方案中：20<x≤30，

∵函数w＝－10(x－35)²＋2 250的图象开口向下，对称轴为直线x＝35，∴当x＝30时，w有最大值，此时w_A最大＝2 000；

B方案中：)

故x的取值范围为45≤x≤49.

∵函数w＝－10(x－35)²＋2 250的图象开口向下，对称轴为直线x＝35，

∴当x＝45时，w有最大值，此时w_B最大＝1 250.

∵w_A最大>w_B最大，∴A方案的最大利润更高．

第203题

如图，在直角坐标系xOy中，二次函数y＝x²＋(2k－1)x＋k＋1的图象与x轴相交于O，A两点．

(1)求这个二次函数的解析式；

参考答案：见解析

解析：

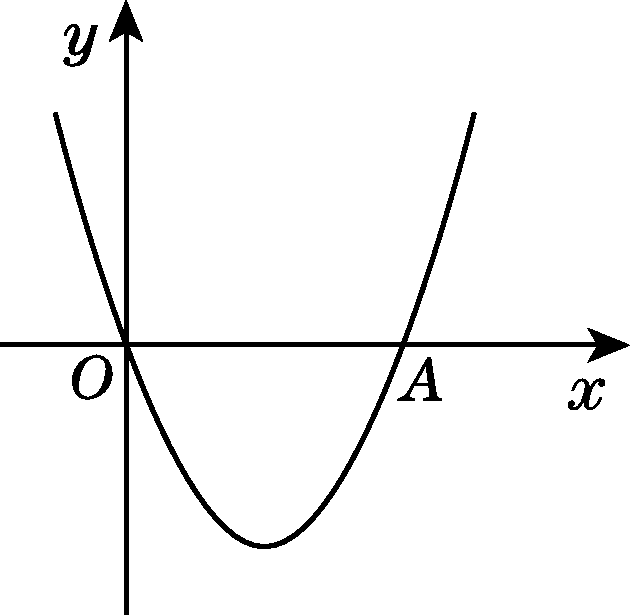
解：(1)∵函数的图象与x轴相交于O，

∴0＝k＋1.

∴k＝－1.

∴y＝x²－3x.

(2)设B点的坐标为(x₀，y₀)．

∵△AOB的面积等于6，

∴2(1)AO·|y₀|＝6.

当x²－3x＝0时，即x(x－3)＝0，解得x＝0或3.

∴AO＝3.

∴|y₀|＝4，即|x₀²－3x₀|＝4.化简得(舍去)．

解得x₀＝4或x₀＝－1(舍去)．

当x₀＝4时，y₀＝x₀²－3x₀＝4，∴点B的坐标为(4，4)．

(3)假设存在点P.设符合条件的点P的坐标为(x₁，x₁²－3x₁)

∵点B的坐标为(4，4)，

∴∠BOA＝45°，BO＝

当∠POB＝90°时，易得点P在直线y＝－x上，

∴x₁²－3x₁＝－x₁.

解得x₁＝2或x₁＝0(舍去)．

∴x₁²－3x₁＝－2.

∴在抛物线上存在点P，使∠POB＝90°，且点P的坐标为(2，－2)．

∴OP＝

∴△POB的面积为2(1)PO·BO＝＝8.

第204题

方程x²－2x＝0的根是(　　)

A.x₁＝x₂＝0

B.x₁＝x₂＝2

C.x₁＝0，x₂＝2

D.x₁＝0，x₂＝－2

参考答案：C

第205题

下列图形中是中心对称图形的有(　　)个．

A.1

B.2

C.3

D.4

参考答案：B

第206题

抛物线y＝x²＋2x＋3的对称轴是(　　)

A.直线x＝1

B.直线x＝－1

C.直线x＝－2

D.直线x＝2

参考答案：B

第207题

如图，△ABC的顶点均在⊙O上，若∠A＝36°，则∠OBC的度数为(　　)

A.18°

B.36°

C.60°

D.54°

参考答案：D

第208题

下列一元二次方程中有两个相等实数根的是(　　)

A.2x²－6x＋1＝0

B.3x²－x－5＝0

C.x²＋x＝0

D.x²－4x＋4＝0

参考答案：D

第209题

如图，在Rt△ABC中，∠BAC＝90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为(　　)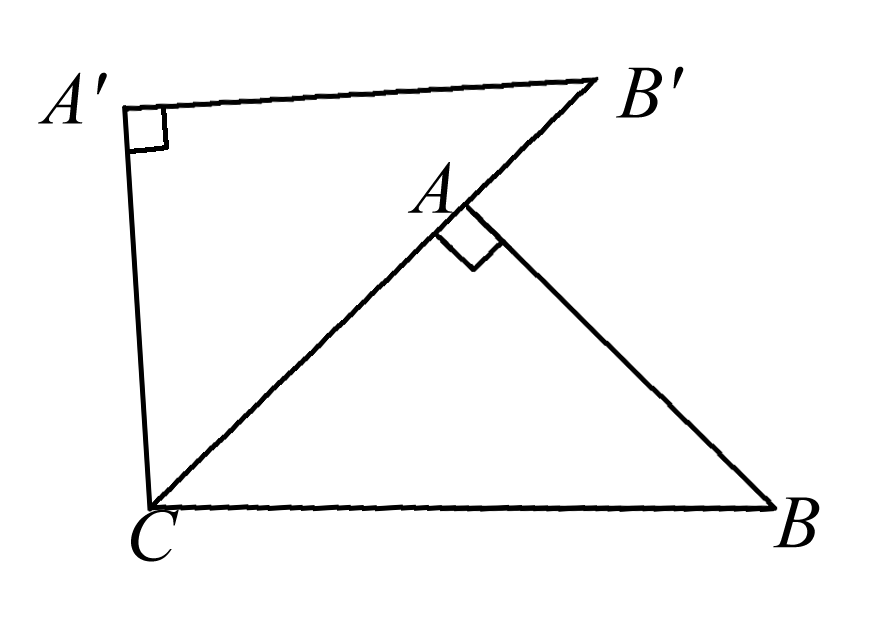

A.42°

B.48°

C.52°

D.58°

参考答案：A

第210题

一个不透明的布袋里装有5个只有颜色不同的球，其中2个红球，3个白球，从布袋中随机摸出一个球，摸出红球的概率是(　　)

A.  

B.  

C.  

D.

参考答案：C

第211题

如图，用一个半径为5 cm的定滑轮带动重物上升，滑轮上一点P旋转了108°，假设绳索(粗细不计)与滑轮之间没有滑动，则重物上升了(　　)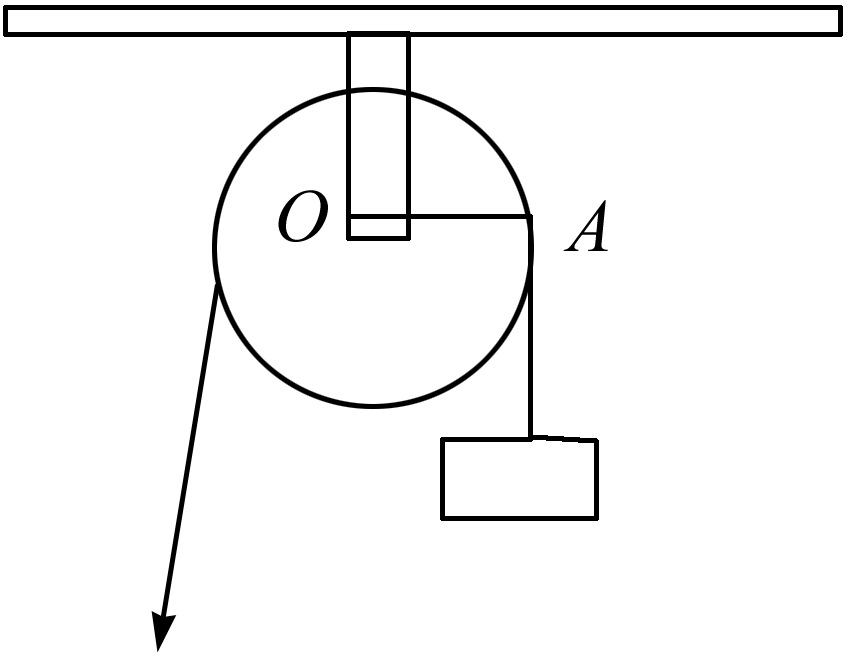

A.π cm

B.2π cm

C.3π cm

D.5π cm

参考答案：C

第212题

如图，在Rt△ABC中，∠ACB＝90°，AC＝2√3，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是(　　)

A.

B.

C.

D.

参考答案：A

第213题

如图是二次函数y＝ax²＋bx＋c的图象，其对称轴为x＝1，下列结论：①abc＞0；②2a＋b＝0；③4a＋2b＋c＜0；④若(－2(3)，y₁)，(3(10)，y₂)是抛物线上两点，则y₁＜y₂，其中结论正确的是(　　)

A.①②

B.②③

C.②④

D.①③④

参考答案：C

第214题

关于x的方程2x²－ax＋1＝0一个根是1，则它的另一个根为________．

参考答案：1/2

解析：

第215题

若一个圆锥的底面圆半径为3 cm，其侧面展开图的圆心角为120°，则圆锥的母线长是______cm.

参考答案：9

第216题

一个不透明的袋子中装有黑、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球都是白球的概率为________．

参考答案：1/4

第217题

如图，在△ACB中，∠BAC＝50°，AC＝2，AB＝3，现将△ACB绕点A逆时针旋转50°得到△AC₁B₁，则阴影部分的面积为______．

参考答案：(5/4)π

解析：

第218题

若二次函数y＝2x²－4x－1的图象与x轴交于A(x₁，0)，B(x₂，0)两点，则的值为________．

参考答案：－4

第219题

《九章算术》是东方数学思想之源，该书中记载：“今有勾八步，股一十五步，问勾中容圆径几何．”其意思为：“今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形内切圆的直径是多少步．”该问题的答案是________步．

参考答案：6

第220题

已知当x₁＝a，x₂＝b，x₃＝c时，二次函数y＝2(1)x²＋mx对应的函数值分别为y₁，y₂，y₃，若正整数a，b，c恰好是一个三角形的三边长，且当a＜b＜c时，都有y₁＜y₂＜y₃，则实数m的取值范围是________．

参考答案：m>-(5/2)

解析：

m>－2(5)　点拨：方法一：∵正整数a，b，c恰好是一个三角形的三边长，且a＜b＜c，∴a最小是2，∵y₁＜y₂＜y₃，∴－＜2.5，解得m＞－2.5.方法二：当a＜b＜c时，都有y₁＜y₂＜y₃，

即)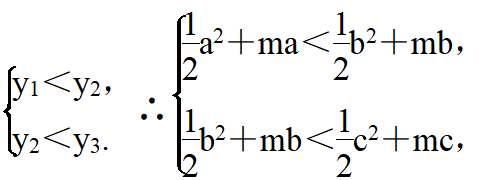

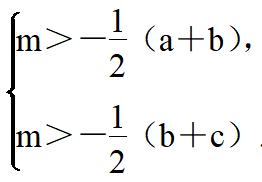∴∵a，b，c恰好是一个三角形的三边长，a＜b＜c，∴a＋b＜b＋c，∴m＞－2(1)(a＋b)，∵a，b，c为正整数，∴a，b，c的最小值分别为2，3，4，∴m＞－2(1)(a＋b)≥－2(1)(2＋3)＝－2(5)，∴m＞－2(5)，故答案为m＞－2(5).

)