“微信扫一扫”进入考试题库练习及模拟考试
九年级（上）期末数学试卷集(328题)
无解，则m的值为（ ）
参考答案：见解析
解析：
（1）∵AD⊥BC，CE⊥AB ∴∠AEF=∠CEB=90° 即∠AFE+∠EAF=∠CFD+∠ECB=90°
又∵∠AEF=∠CFD ∴∠EAF=∠ECB
在△AEF和△CEB中，∠AEF=∠CEB，AE=CE，∠EAF=∠ECB
∴△AEF≌△CEB （6分）
（2）由△AEF≌△CEB得：AF=BC 在△ABC中，AB=AC，AD⊥BC
∴CD=BD，BC=2CD
∴AF=2CD. （4分）
第251题
（10分）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE． 求证：（1）△AEF≌△CEB； （2）AF=2CD．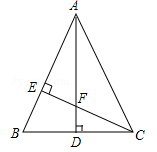
参考答案：见解析
解析：
（1） 画图 3分 A1（2,3） （2分）
（2） （-2，-3） （2分）
（3） （-5,3） （-5，-3） （-2，-3） （3分）
第252题
（10分）．有两块面积相同的试验田，分别收获蔬菜900kg和1500kg，已知第一块试验田每亩收获蔬菜比第二块少300kg，求第一块试验田每亩收获蔬菜多少千克？
参考答案：见解析
解析：
解：设第一块试验田每亩收获蔬菜x千克，由题意得：（1分）
， （4分）
解得：x=450， （2分）
经检验：x=450是原分式方程的解， （2分）
答：第一块试验田每亩收获蔬菜450千克． （1分）
参考答案：见解析
解析：
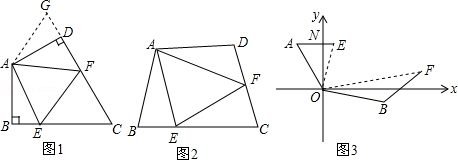
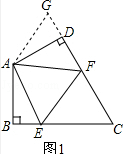
（1）EF=BE+DF；（2分）
（2）EF=BE+DF仍然成立．（1分）
证明：如图2，延长FD到G，使DG=BE，连接AG， ∵∠B+∠ADC=180°，∠ADC+∠ADG=180°，
∴∠B=∠ADG，在△ABE和△ADG中，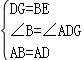 
， ∴△ABE≌△ADG（SAS）， （2分）
∴AE=AG，∠BAE=∠DAG，
∵∠EAF=
∠BAD， ∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF， ∴∠EAF=∠GAF，
在△AEF和△GAF中，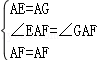 
， ∴△AEF≌△GAF（SAS）， （2分）
∴EF=FG， ∵FG=DG+DF=BE+DF，
∴EF=BE+DF； （1分）
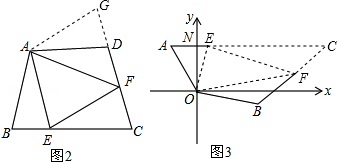
（3）E、F之间的距离是583米。 （1分）
如图3，连接EF，延长AE、BF相交于点C，
∵∠AOB=（90°﹣70°）°+90°+（90°﹣60°）=140°，∠EOF=70°，
∴∠EOF=∠AOB，
又∵OA=OB， ∠OAC+∠OBC=（90°﹣20°+50°）+60°=180°，
∴符合探索延伸中的条件， ∴结论EF=AE+BF成立， 即EF=583米． （3分）
第255题 一个不透明的袋子中装有5个黑球和3个白球，这些球的大小、质地完全相同，随机从袋子中摸出4个球，则下列事件是必然事件的是
A.摸出的四个球中至少有一个球是黑球
B.摸出的四个球中至少有一个球是白球
C.摸出的四个球中至少有两个球是黑球
D.摸出的四个球中至少有两个球是白球
参考答案：A
