第261题

如图，在Rt△ABC中，∠BAC=90°．如果将该三角形绕点A按顺时针方向旋转到△AB₁C₁的位置，点B₁恰好落在边BC的中点处．那么旋转的角度等于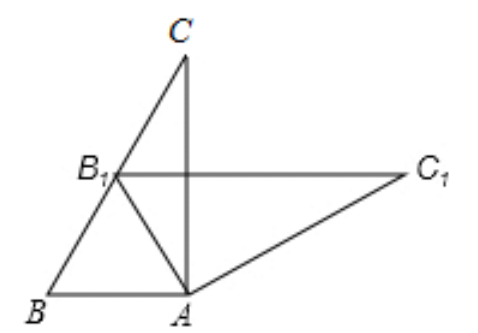

A.80°

B.65°

C.60°

D.55°

参考答案：C

第262题

一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此圆锥的底面半径为

A.cm

B.cm

C.3cm

D.cm

参考答案：A

第263题

甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是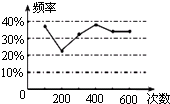

A.掷一枚正六面体的骰子，出现1点的概率

B.从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率

C.抛一枚硬币，出现正面的概率

D.任意写一个整数，它能被2整除的概率

参考答案：B

第264题

某方便面厂10月份生产方便面100吨，这样1至10月份生产量恰好完成全年的生产任务，为了满足市场需要，计划到年底再生产231吨方便面，则11、12月的月平均增长率为

A.10%

B.31%

C.13%

D.11%

参考答案：A

第265题

如图，在菱形ABCD中，DE⊥AB，cosA＝，BE=2，则BD的值

A.2

B.√5

C.2√5

D.5

参考答案：C

第266题

已知函数y=的图象如图，以下结论：①m＜0；②在每个分支上y随x的增大而增大；③若点A（-1，a）、点B（2，b）在图象上，则a＜b；④若点P（m，n）在图象上，则点P₁（-m，-n）也在图象上．其中正确的个数是

A.4个

B.3个

C.2个

D.1个

参考答案：B

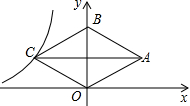
第267题

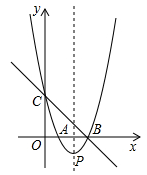
如图，Rt△OAB的顶点A（-2，4）在抛物线y=ax²上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为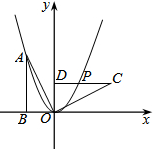

A.（√2，√2）

B.（2，2）

C.（√2，2）

D.（2，√2）

参考答案：C

第268题

计算：sin30°+cos30°•tan60°=               ．

参考答案：2

第269题

从地面竖直向上抛出一个小球，小球的高度h（米）与运动时间t（秒）之间的关系式为h=30t-5t²，那么小球抛出           秒后达到最高点．

参考答案：3

第270题

边长为1的正六边形的边心距是           ．

参考答案：√(3)/2

解析：

第271题

如图，菱形OABC的顶点O是原点，顶点B在y轴上，菱形的两条对角线的长分别是6和4，反比例函数y＝(x＜0)的图象经过点C，则k的值为       ．

参考答案：-6

第272题

如图，在等边△ABC中，D为BC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的边长为          ．

参考答案：9

第273题

已知x=-2是关于x的方程2x²+ax-a²=0的一个根，求a的值．

参考答案：见解析

解析：

解：当x=-2时，8-2a-a²=0，...........................................2分

即：a²+2a-8=0，.................................................................3分

∴，...........................5分

∴a₁=2，a₂=-4．........................................................................7分

第274题

经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．

（1）请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果；

参考答案：见解析

解析：

解：（1）（5分）两辆汽车所有9种可能的行驶方向如下：

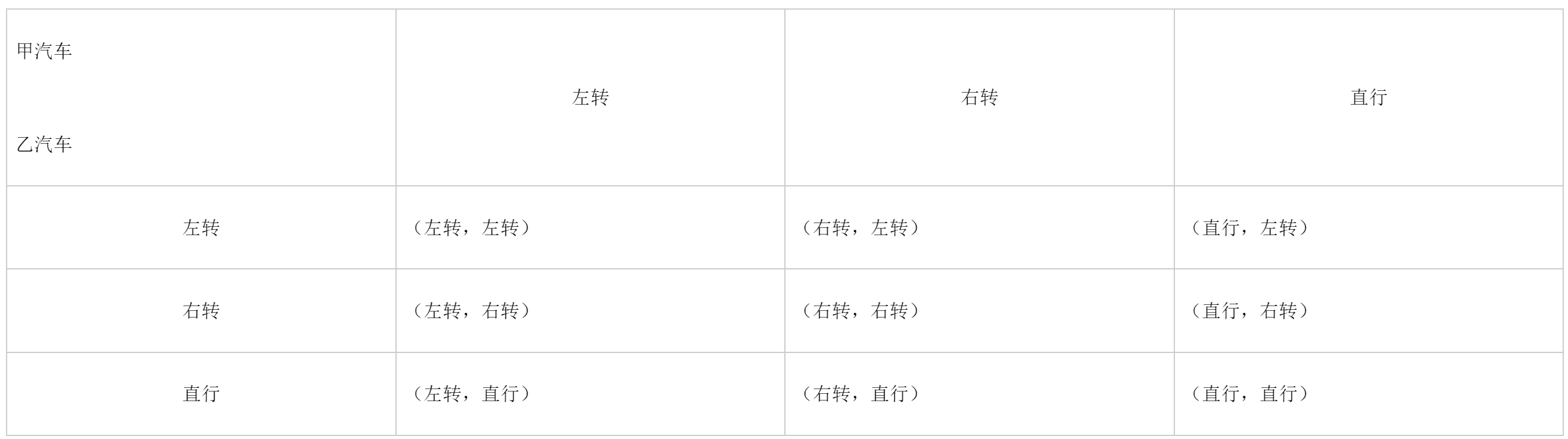
（2）（3分）由上表知：两辆汽车都向左转的概率是：．

第275题

如图是一次“测量旗杆高度”的活动场景抽象出的平面几何图形．活动中测得的数据如下：

参考答案：见解析

解析：

解：解法一，选用①②④，...............................................................................3分

∵AB⊥FC，CD⊥FC，

∴∠ABF=∠DCE=90°，..................................................................................4分

又∵AF∥DE，

∴∠AFB=∠DEC，.........................................................................................5分

∴△ABF∽△DCE，........................................................................................6分

∴，...............................................................................................7分

又∵DC=1.5m，FB=7.6m，EC=1.7m，

∴AB=6.7m．

即旗杆高度是6.7m．......................................................................................8分

解法二，选①③⑤．............................................................................................3分

过点D作DG⊥AB于点G．

∵AB⊥FC，DC⊥FC，

∴四边形BCDG是矩形，................................................................................4分

∴CD=BG=1.5m，DG=BC=9m，.....................................................................5分

在直角△AGD中，∠ADG=30°，

∴tan30°=，................................................................................................6分

∴AG=，.....................................................................................................7分

又∵AB=AG+GB，

∴AB=≈6.7m．

即旗杆高度是6.7m．.........................................................................................8分

第276题

在平面直角坐标系中，已知反比例函数y=的图象经过点A，点O是坐标原点，OA=2且OA与x轴的夹角是60°．

（1）试确定此反比例函数的解析式；

参考答案：见解析

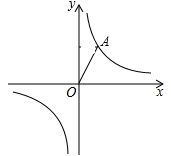
解析：

解：（1）（4分）由题意的点A的坐标是（1，），....................2分

把A（1，）代入y=，

得k=1×=，.............................................................. ...3分

∴反比例函数的解析式为y=；.......................................4分

（2）（5分）点B在此反比例函数的图象上．..............................1分

理由如下：过点B作x轴的垂线交x轴于点D，

∵线段OA绕O点顺时针旋转30°得到线段OB，

∴∠AOB=30°，OB=OA=2，∴∠BOD=30°，.......................2分

在Rt△BOD中，BD=OB=1，OD=BD=，............3分

∴B点坐标为（，1），.....................................................4分

∵当x=时，y==1，

∴点B（，1）在反比例函数y＝的图象上．.................5分

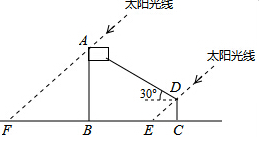
第277题

如图是某超市地下停车场入口的设计图，请根据图中数据计算CE的长度．（结果保留小数点后两位；参考数据：sin22°=0.3746，cos22°=0.9272，tan22°=0.4040）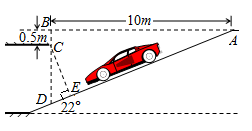

参考答案：见解析

解析：

解：由已知有：∠BAE=22°，∠ABC=90°，∠CED=∠AEC=90°

∴∠BCE=158°，∴∠DCE=22°，...............................................................2分

又∵tan∠BAE=，

∴BD=AB•tan∠BAE，...............................................................................4分

又∵cos∠BAE=cos∠DCE=，..........................................................5分

∴CE=CD•cos∠BAE

=（BD-BC）•cos∠BAE.................................................................6分

=（ AB•tan∠BAE-BC）•cos∠BAE...............................................7分

=（10×0.4040-0.5）×0.9272

≈3.28（m）．..................................................................................8分

第278题

如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=2，ED=4，

（1）求证：△ABE∽△ADB，并求阴影部分的面积；

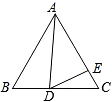
参考答案：见解析

解析：

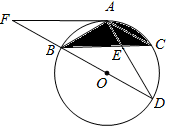
（1）（7分）证明：∵AB=AC，∴∠ABC=∠C，

∵∠C=∠D，∴∠ABC=∠D，

又∵∠BAE=∠EAB，

∴△ABE∽△ADB，...........................................................2分

∴，

∴AB²=AD•AE=（AE+ED）•AE=（2+4）×2=12，

∴AB=．....................................................................3分

∵BD为⊙O的直径，∴∠BAD=90°

∴

∴∠ABE=30°..................................................................5分

∴∠ADB=30°

∴∠CBD=30°，∴AC//BD.......................................6分

连接OA，OB，∴OA=，∠AOC=60°

∴........................7分

（2）（4分）直线FA与⊙O相切，.........................................................1分

理由如下：

∵∠ABC=30°，AB=AC，

∴∠C=30°，∴∠AOB=60°，

∴.是等边三角形..............................................................2分

∴AB=BO，∠BAO=∠ABO=60°，

∴∠FAB=∠ABO=30°，∴∠OAF=90°，........................................3分

∴直线FA与⊙O相切．..............................................................................4分

第279题

如图，直线y=-x+3与x轴、y轴分别交于点

B、点C，经过B、C两点的抛物线y=x²+bx+c与x轴的另一个交点为A，顶点为P．

参考答案：见解析

解析：

解：（1）（6分）由已知，得B（3，0），C（0，3），..............2分

∴，..................................................................4分

解得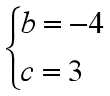，..........................................................................5分

∴抛物线解析式为y=x²-4x+3；....................................................6分

（2）由（1），得A（1，0），连接BP，................................1分

∵∠CBA=∠ABP=45°，

∴当时，△ABC∽△PBQ，

∴BQ=3，∴Q₁（0，0），.........................................................3分

∴当时，△ABC∽△QBP，

∴BQ=，∴Q₂（，0）；..................................................5分

∴Q点的坐标是（0，0）或（，0）．..............................6分

第280题

下列手机软件图标中，既是轴对称图形又是中心对称图形的是(　　)

A.A

B.B

C.C

D.D

参考答案：D