“微信扫一扫”进入题库练习及模拟考试
九年级（上）期末数学试卷集（328题）
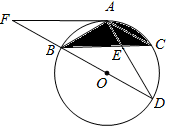
如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=2，ED=4，
（1）求证：△ABE∽△ADB，并求阴影部分的面积；
（2）延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．
知识点：试卷11
参考答案：见解析
解析：
（1）（7分）证明：∵AB=AC，∴∠ABC=∠C，
∵∠C=∠D，∴∠ABC=∠D，
又∵∠BAE=∠EAB，
∴△ABE∽△ADB，...........................................................2分
∴
，
∴AB2=AD•AE=（AE+ED）•AE=（2+4）×2=12，
∴AB=
．....................................................................3分
∵BD为⊙O的直径，∴∠BAD=90°
∴
∴∠ABE=30°..................................................................5分
∴∠ADB=30°
∴∠CBD=30°，∴AC//BD.......................................6分
连接OA，OB，∴OA=，∠AOC=60°
∴
........................7分
（2）（4分）直线FA与⊙O相切，.........................................................1分
理由如下：
∵∠ABC=30°，AB=AC，
∴∠C=30°，∴∠AOB=60°，
∴
.是等边三角形..............................................................2分
∴AB=BO，∠BAO=∠ABO=60°，
∴∠FAB=
∠ABO=30°，∴∠OAF=90°，........................................3分
∴直线FA与⊙O相切．..............................................................................4分