“微信扫一扫”进入考试题库练习及模拟考试
九年级(上)期末数学试卷集(328题)
第223题
(7分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. (1)求证:△BDE≌△BCE; (2)试判断四边形ABED的形状,并说明理由.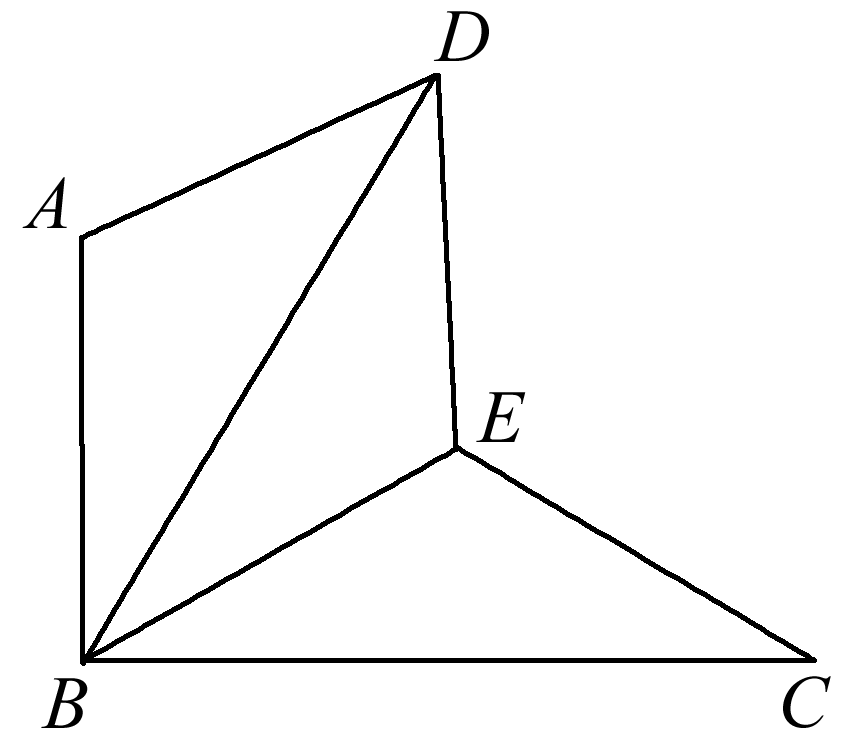
参考答案:见解析
解析:
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,∴DB=CB,∠ABD=∠EBC,∠ABE=60°,∵AB⊥BC,∴∠ABC=90°,
∴∠DBE=∠CBE=30°,在△BDE和△BCE中,
∵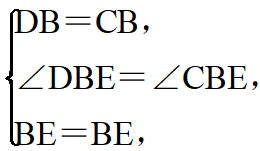
∴△BDE≌△BCE.
(2)四边形ABED为菱形.理由如下:由(1)得△BDE≌△BCE,∵△BAD是由△BEC旋转而得,∴△BAD≌△BEC,∴BA=BE,AD=EC=ED,又∵BE=CE,∴BE=ED,∴四边形ABED为菱形.
参考答案:见解析
解析:
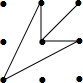
(1)画树状图为:
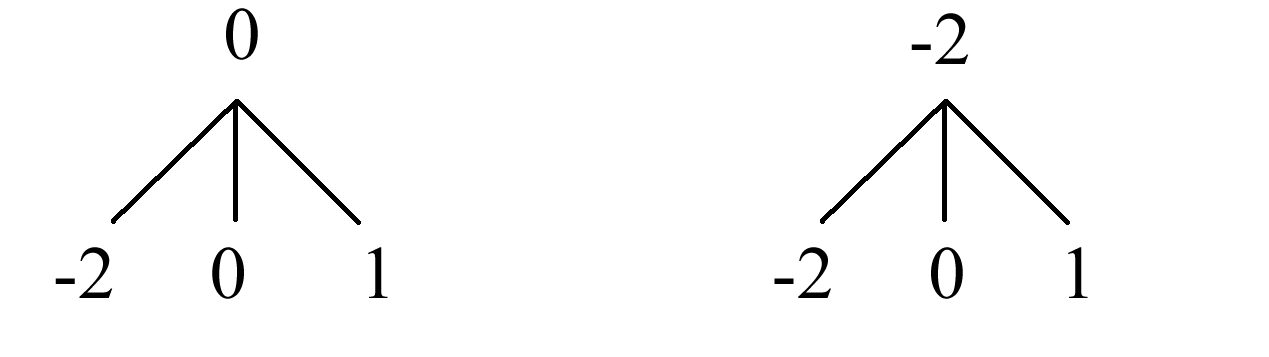
共有6种等可能的结果数,它们为(0,-2),(0,0),(0,1),(-2,-2),(-2,0),(-2,1).(2)点Q在x轴上的结果数为2,所以点Q在x轴上的概率为6=3.
参考答案:见解析
解析:
(1)∵原方程有两个实数根,
∴[-(2k+1)]2-4(k2+2k)≥0,∴k≤4,
∴当k≤4时,原方程有两个实数根.
(2)不存在实数k,使得x1·x2-x12-x22≥0成立.理由如下:
假设存在实数k,使得x1·x2-x12-x22≥0成立.
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1·x2=k2+2k.由x1·x2-x12-x22≥0,得3x1·x2-(x1+x2)2≥0,∴3(k2+2k)-(2k+1)2≥0,整理得-(k-1)2≥0,
∴只有当k=1时,不等式才能成立.又∵由(1)知k≤4,
∴不存在实数k,使得x1·x2-x12-x22≥0成立.
参考答案:见解析
解析:
(1)设围成的矩形一边长为x米,则矩形的另一边长为(16-x)米.依题意得y=x(16-x)=-x2+16x,故y关于x的函数解析式是y=-x2+16x.
(2)由(1)知,y=-x2+16x.当y=60时,-x2+16x=60,解得x1=6,x2=10,即当x是6或10时,围成的养鸡场面积为60平方米.
(3)不能围成面积为70平方米的养鸡场.理由如下:由(1)知,y=-x2+16x.当y=70时,-x2+16x=70,即x2-16x+70=0,因为Δ=(-16)2-4×1×70=-24<0,所以该方程无实数解.故不能围成面积为70平方米的养鸡场.
第227题
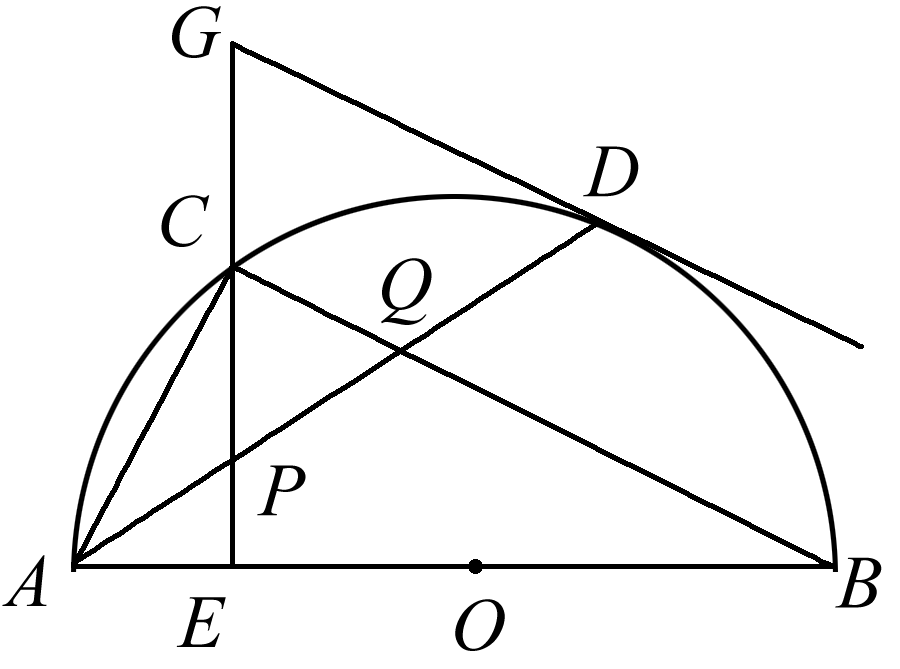
(9分)如图,AB是⊙O的直径,ED=BD,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C. (1)若OA=CD=2√2,求阴影部分的面积; (2)求证:DE=DM.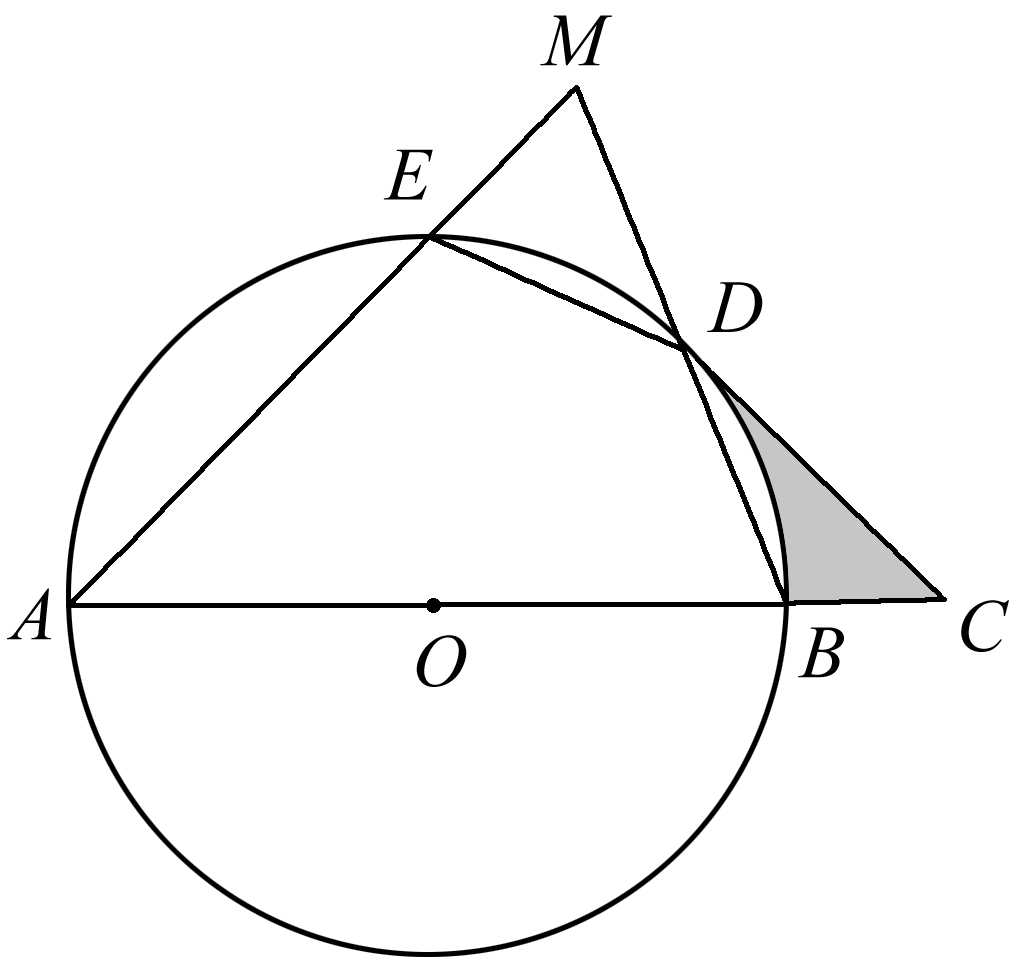
参考答案:见解析
解析:
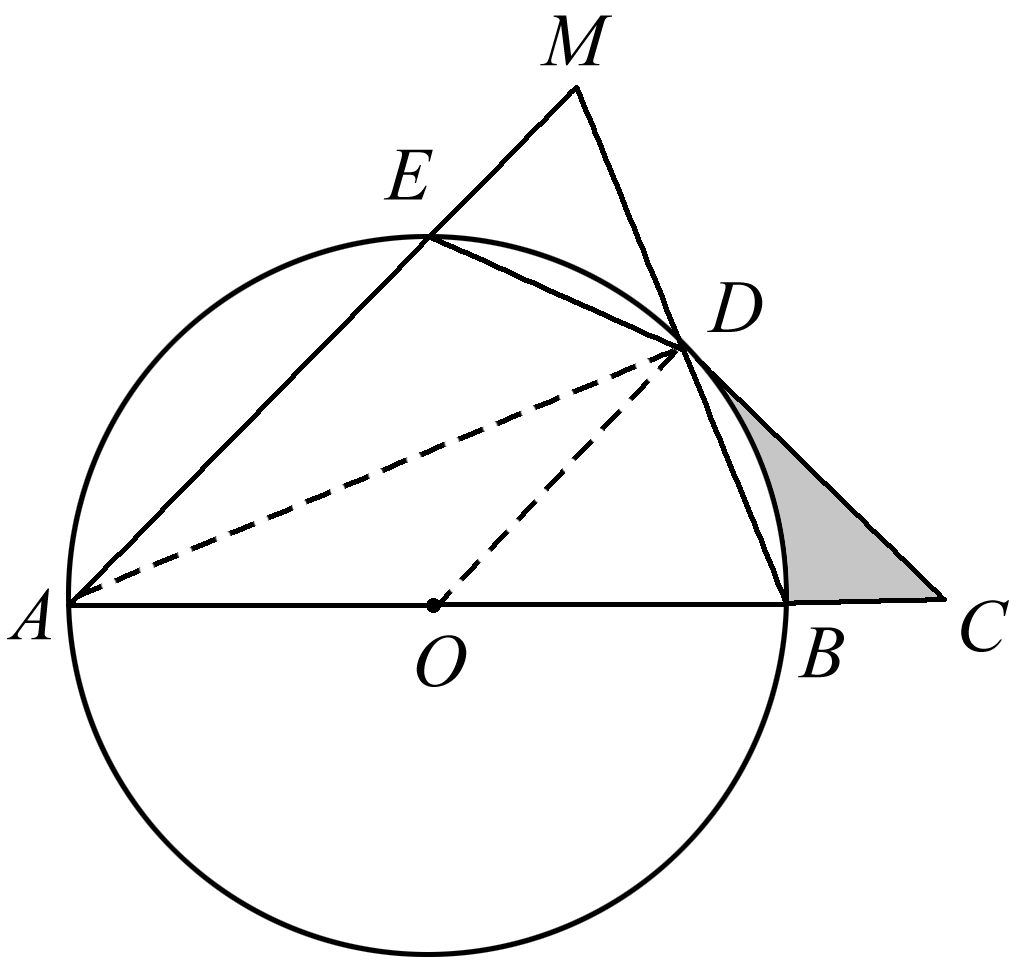
(1)如图,连接OD,∵CD是⊙O切线,∴OD⊥CD,∵OA=CD=2√2,OA=OD,∴OD=CD=2√2,∴△OCD为等腰直角三角形,∴∠DOC=∠C=45°,
∴S阴影=S△OCD-S扇形OBD=
![]() =4-π.
=4-π.
(2)证明:如图,连接AD,∵AB是⊙O直径,∴∠ADB=∠ADM=90°,
又∵ED=BD,∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
∴△AMD≌△ABD,∴DM=BD,∴DE=DM.
参考答案:见解析
解析:
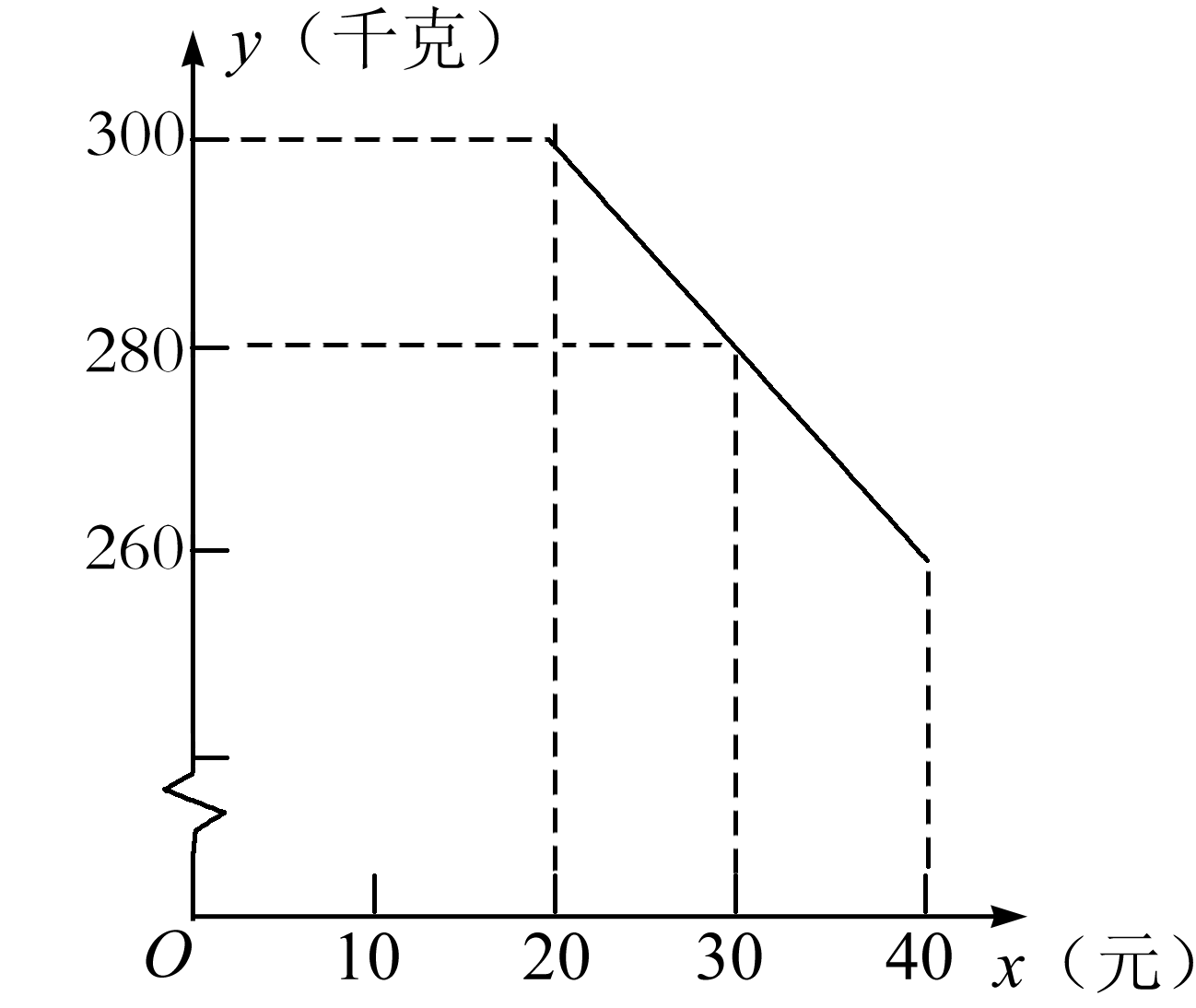
(1)设y与x的函数解析式为y=kx+b,根据题意,
得![]() 解得
解得![]()
∴y与x的函数解析式为y=-2x+340(20≤x≤40).
(2)由已知得W=(x-20)(-2x+340)=-2x2+380x-6 800=-2(x-95)2+11 250,
∵-2<0,
∴当x≤95时,W随x的增大而增大,∵20≤x≤40,
∴当x=40时,W最大,最大值为-2(40-95)2+11 250=5 200(元).
参考答案:见解析
解析:
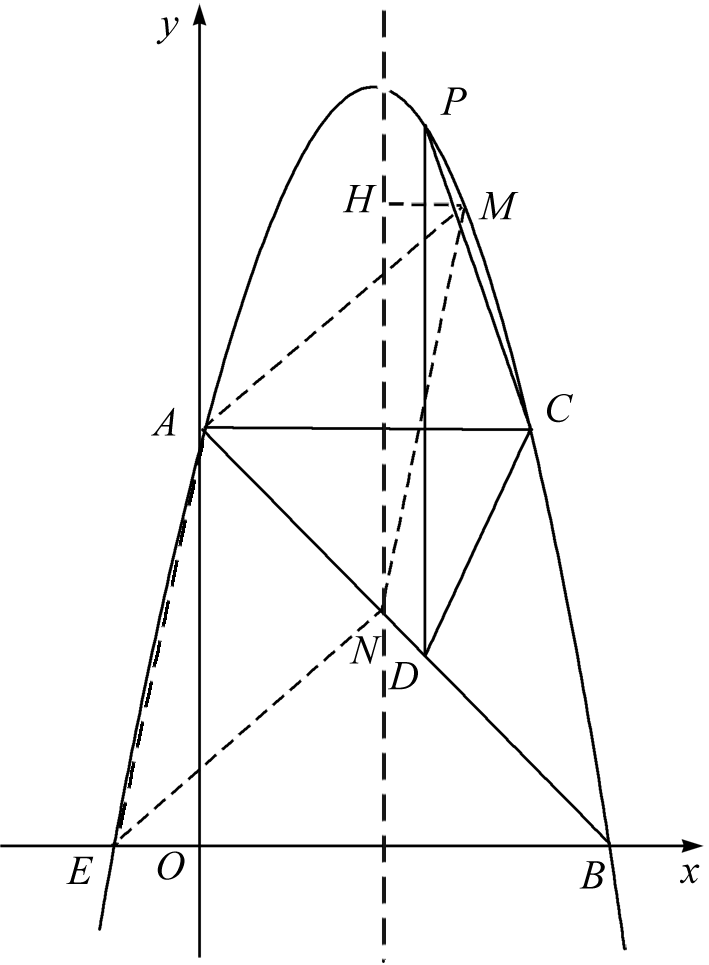
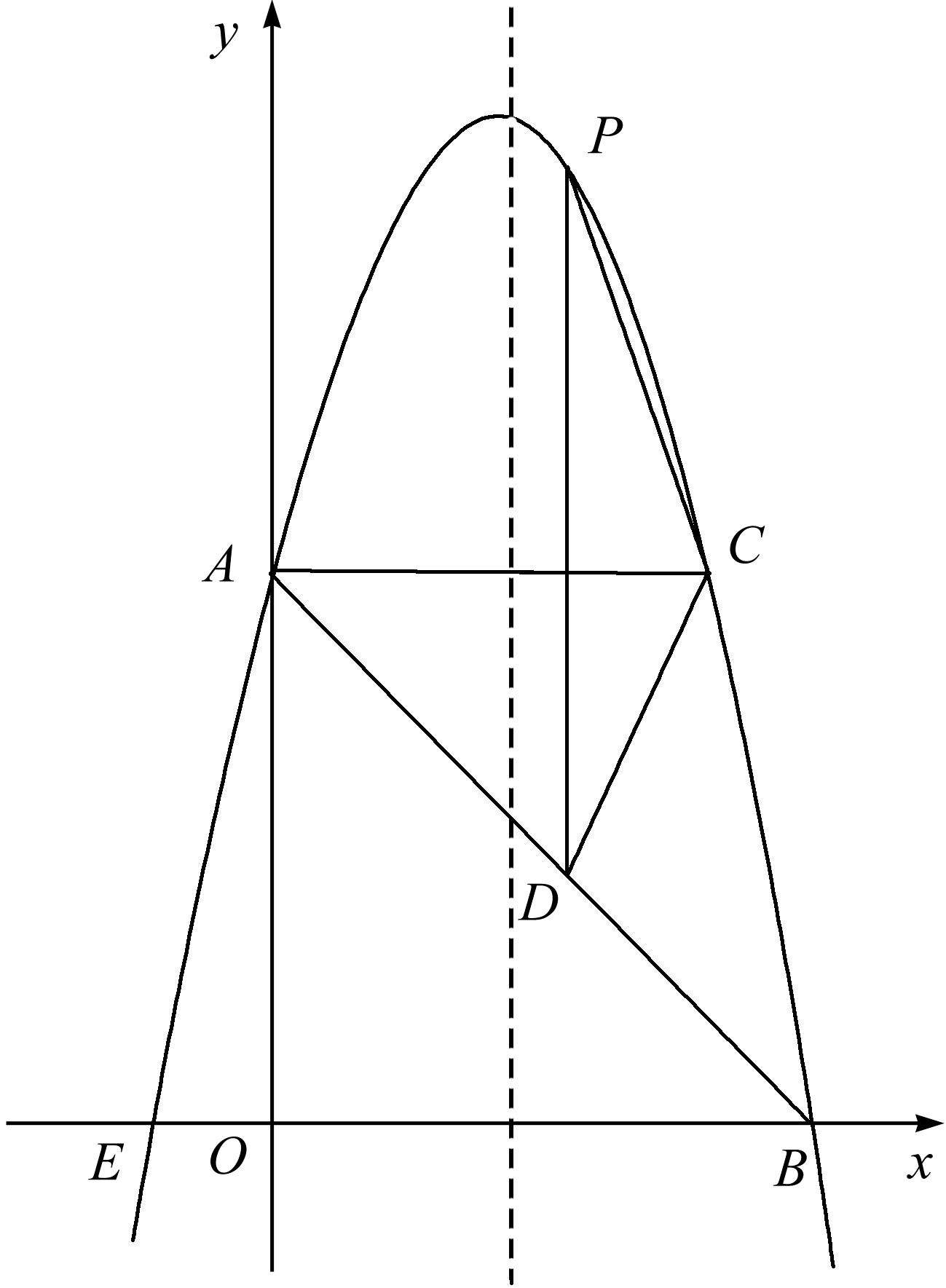
(1)设抛物线解析式为y=a(x-2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=-1,y=-(x-2)2+9=-x2+4x+5.
(2)当y=0时,-x2+4x+5=0,
∴x1=-1,x2=5,
∴E(-1,0),B(5,0),设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=-1,n=5,
∴直线AB的解析式为y=-x+5.设P(x,-x2+4x+5),
∴D(x,-x+5),
∴PD=-x2+4x+5+x-5=-x2+5x,
∵AC=4,
∴S四边形APCD=2×AC×PD=2(-x2+5x)=-2x2+10x,
∴当x=![]() 时,
时,
∴即点![]() 时,S四边形APCD最大=2.
时,S四边形APCD最大=2.
(3)如图,过点M作MH垂直于对称轴,垂足为点H,
∵四边形AENM是平行四边形,
∴MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1.
∴M点的横坐标为x=3或x=1.当x=1时,M点纵坐标为8,当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(-1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴可设直线MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),∵AE2=OA2+OE2=26,
∵MN=AE,∴MN2=AE2,
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴MN2=(1-2)2+[8-(10+b)]2=1+(b+2)2=26,
∴b=3或b=-7,∴10+b=13或10+b=3.
∴当M点的坐标为(1,8)时,N点坐标为(2,13),当M点的坐标为(3,8)时,N点坐标为(2,3).
第233题
根据下列已知条件,能唯一画出△ABC的是( )
A.AB=2,BC=4,AC=7
B.AB=5,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AC=4
D.∠C=90°,AB=6
参考答案:C