九年级（上）期末数学试卷集（328题）

---

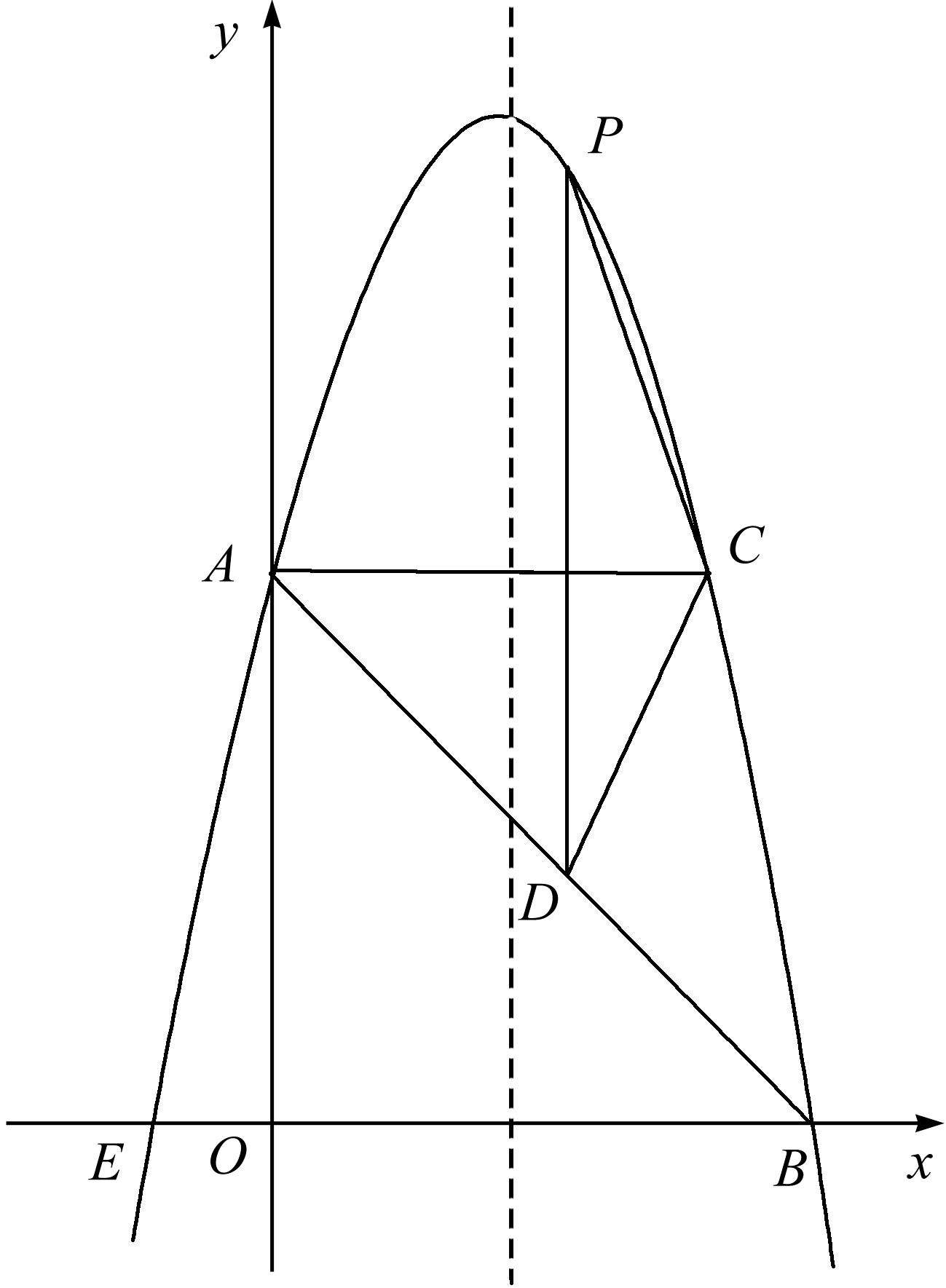
(11分)(2016·泰安)如图，在平面直角坐标系中，抛物线y＝ax²＋bx＋c的顶点坐标为(2，9)，与y轴交于点A(0，5)，与x轴交于点E，B.

(1)求二次函数y＝ax²＋bx＋c的解析式；

(2)过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点(点P在AC上方)，作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；

(3)若点M在抛物线上，点N在其对称轴上，使得以A，E，N，M为顶点的四边形是平行四边形，且AE为其一边，求点M，N的坐标．

知识点：试卷09

参考答案：见解析

解析：

(1)设抛物线解析式为y＝a(x－2)²＋9，

∵抛物线与y轴交于点A(0，5)，

∴4a＋9＝5，

∴a＝－1，y＝－(x－2)²＋9＝－x²＋4x＋5.

(2)当y＝0时，－x²＋4x＋5＝0，

∴x₁＝－1，x₂＝5，

∴E(－1，0)，B(5，0)，设直线AB的解析式为y＝mx＋n，

∵A(0，5)，B(5，0)，

∴m＝－1，n＝5，

∴直线AB的解析式为y＝－x＋5.设P(x，－x²＋4x＋5)，

∴D(x，－x＋5)，

∴PD＝－x²＋4x＋5＋x－5＝－x²＋5x，

∵AC＝4，

∴S_{四边形APCD}＝2(1)×AC×PD＝2(－x²＋5x)＝－2x²＋10x，

∴当x＝时，

∴即点时，S_{四边形APCD最大}＝2(25).

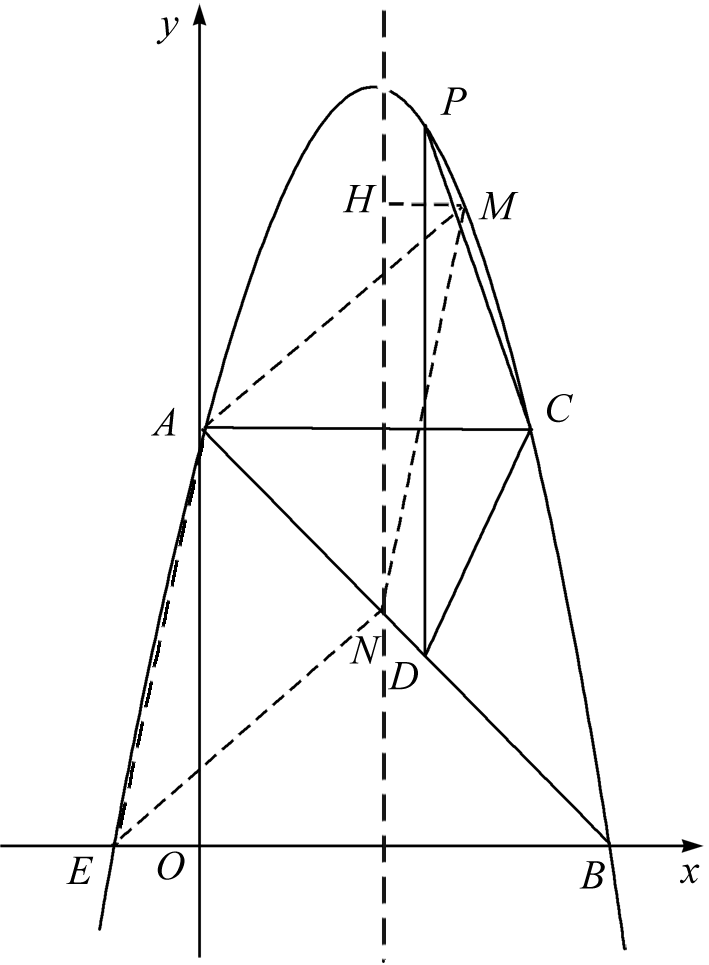
(3)如图，过点M作MH垂直于对称轴，垂足为点H，

∵四边形AENM是平行四边形，

∴MN∥AE，MN＝AE，

∴△HMN≌△AOE，

∴HM＝OE＝1.

∴M点的横坐标为x＝3或x＝1.当x＝1时，M点纵坐标为8，当x＝3时，M点纵坐标为8，

∴M点的坐标为M₁(1，8)或M₂(3，8)，

∵A(0，5)，E(－1，0)，

∴直线AE解析式为y＝5x＋5，

∵MN∥AE，

∴可设直线MN的解析式为y＝5x＋b，

∵点N在抛物线对称轴x＝2上，

∴N(2，10＋b)，∵AE²＝OA²＋OE²＝26，

∵MN＝AE，∴MN²＝AE²，

∵M点的坐标为M₁(1，8)或M₂(3，8)，

∴点M₁，M₂关于抛物线对称轴x＝2对称，

∵点N在抛物线对称轴上，

∴M₁N＝M₂N，

∴MN²＝(1－2)²＋[8－(10＋b)]²＝1＋(b＋2)²＝26，

∴b＝3或b＝－7，∴10＋b＝13或10＋b＝3.

∴当M点的坐标为(1，8)时，N点坐标为(2，13)，当M点的坐标为(3，8)时，N点坐标为(2，3)．