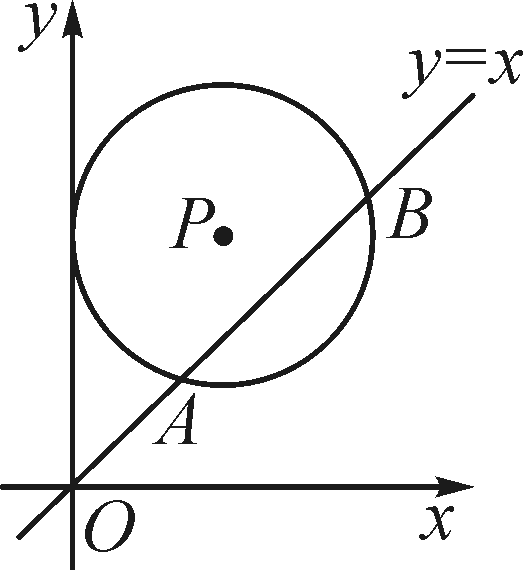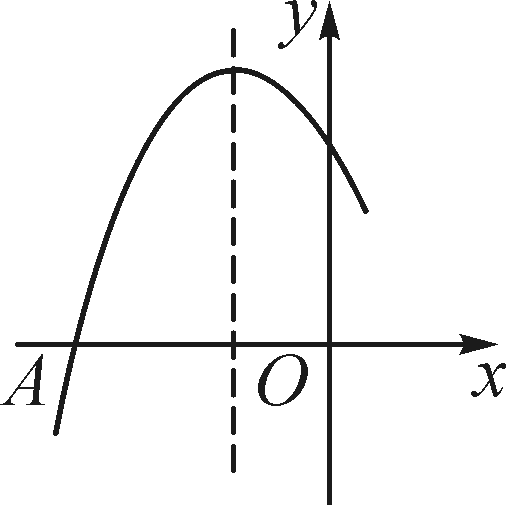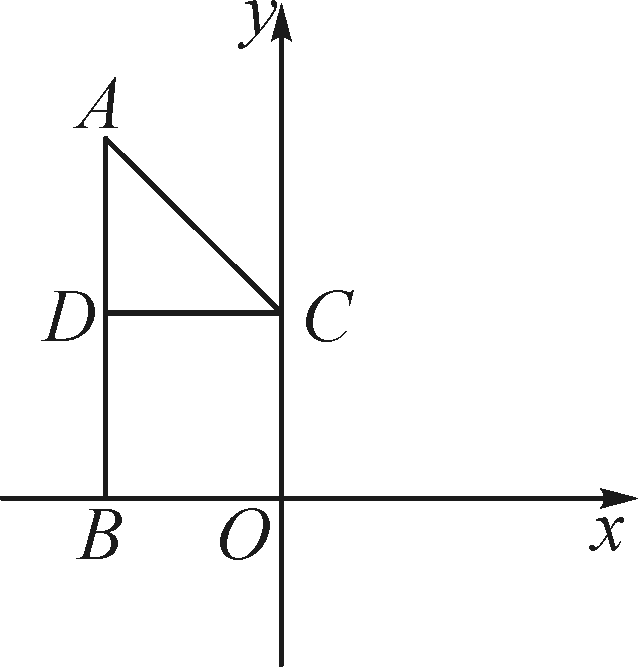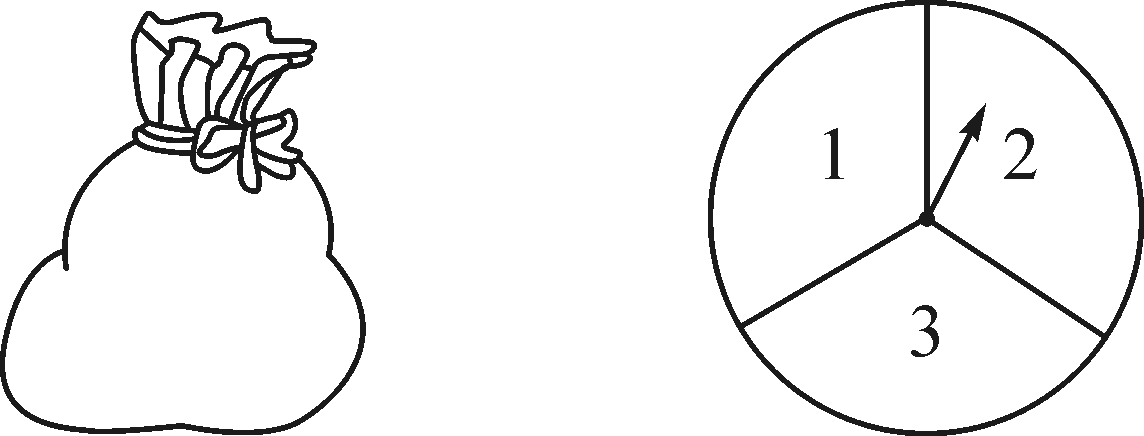第161题

如图，△ABC中，∠BAC＝33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为____．

参考答案：17°

第162题

若实数a，b满足(4a＋4b)(4a＋4b－2)－8＝0，则a＋b＝____．

参考答案：－1/2或1

第163题

若|b－1|＋＝0，且一元二次方程kx²＋ax＋b＝0有两个实数根，则k的取值范围是____.

参考答案：k≤4且k≠0

第164题

如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON＝90°,OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为___．

参考答案：1/4

第165题

如图，已知圆锥的高为√3，高所在直线与母线的夹角为30°，则圆锥的侧面积为____.

参考答案：2π

第166题

公路上行驶的汽车急刹车时，刹车距离s(m)与时间t(s)的函数关系式为s＝20t－5t²，当遇到紧急情况时，司机急刹车，但由于惯性汽车要滑行____m才能停下来．

参考答案：20

第167题

如图，在平面直角坐标系中，⊙P的圆心是(2，a)(a＞2)，半径为2，函数y＝x的图象被⊙P截得的弦AB的长为2√3，则a的值是____．

参考答案：2＋√2

第168题

如图是二次函数y＝ax²＋bx＋c图象的一部分，图象过点A(－3，0)，对称轴为直线x＝－1，给出以下结论：

①abc<0；

参考答案：②③⑤

第169题

(6分)先化简，再求值：，其中x满足x²－3x＋2＝0.

参考答案：见解析

解析：

解：原式==x，∵x2－3x＋2＝0，∴(x－2)(x－1)＝0，∴x＝1或x＝2，当x＝1时，(x－1)2＝0，分式无意义，∴x＝2，原式＝2

第170题

关于x的一元二次方程x²＋(2k＋1)x＋k²＋1＝0有两个不等实根x₁，x₂.

(1)求实数k的取值范围；

参考答案：见解析

解析：

解：(1)∵原方程有两个不相等的实数根，∴Δ＝(2k＋1)2－4(k2＋1)>0，解得k>4(3)

(2)根据根与系数的关系得x1＋x2＝－(2k＋1)，x1x2＝k2＋1，又∵x1＋x2＝－x1x2，∴－(2k＋1)＝－(k2＋1)，解得k1＝0，k2＝2，∵k>4(3)，∴k的值为2

第171题

(7分)如图，将小旗ACDB放于平面直角坐标系中，得到各顶点的坐标为A(－6，12)，B(－6，0)，C(0，6)，D(－6，6)．以点B为旋转中心，在平面直角坐标系内将小旗顺时针旋转90°.

参考答案：见解析

解析：

解：(1)图略

(2)点A′(6，0)，C′(0，－6)，D′(0，0)

(3)∵A(－6，12)，B(－6，0)，∴AB＝12，∴线段BA旋转到B′A′时所扫过的扇形的面积＝360(90π×122)＝36π

第172题

(8分)一个不透明的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，另有一个可以自由旋转的圆盘，被分成面积相等的3个扇形区域，分别标有数字1，2，3(如图)．小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一个人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于4，那么小颖去，否则小亮去．

(1)用画树状图或列表法求出小颖参加比赛的概率；

参考答案：见解析

解析：

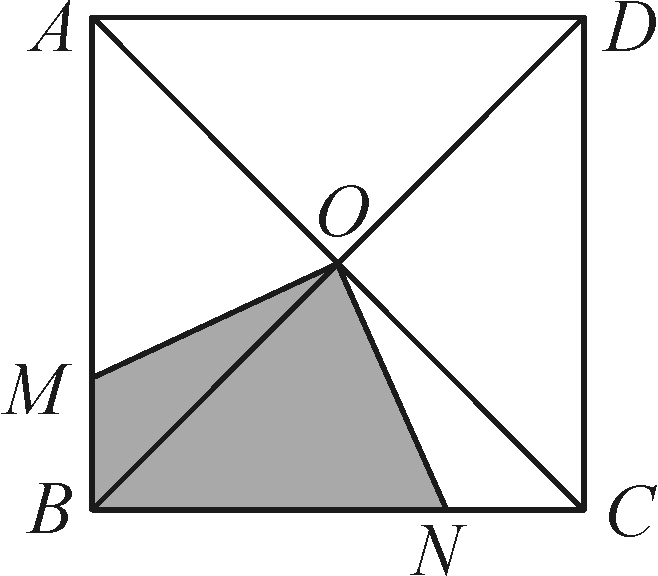
解：(1)画树状图略，∵共有12种等可能的结果，数字之和小于4的有3种情况，∴P(和小于4)＝12(3)＝4(1)，∴小颖参加比赛的概率为4(1)　(2)不公平，∵P(和不小于4)＝4(3)，∴P(和小于4)≠P(和不小于4)，∴游戏不公平．游戏规则可改为：若数字之和为偶数，则小颖去；若数字之和为奇数，则小亮去

第173题

(8分)如图，某足球运动员站在点O处练习射门，将足球从离地面0.5 m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at²＋5t＋c，已知足球飞行0.8 s时，离地面的高度为3.5 m.

(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？

参考答案：见解析

解析：

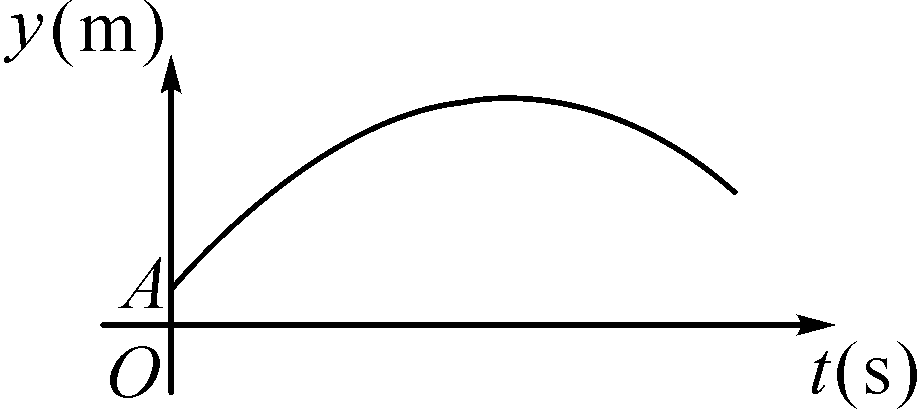
解：(1)抛物线的解析式为y＝－16(25)t2＋5t＋2(1)，∴当t＝5(8)时，y最大＝4.5　(2)把x＝28代入x＝10t得t＝2.8，∴当t＝2.8时，y＝－16(25)×2.82＋5×2.8＋2(1)＝2.25＜2.44，∴他能将球直接射入球门

第174题

如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE.

(1)求证：DE是⊙O的切线；

参考答案：见解析

解析：

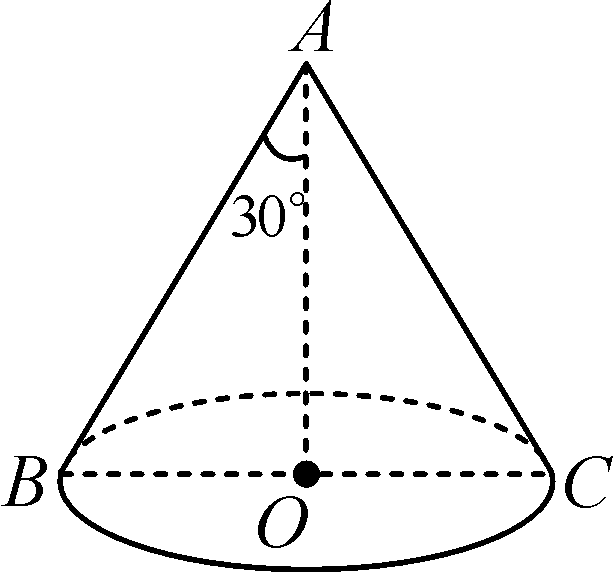
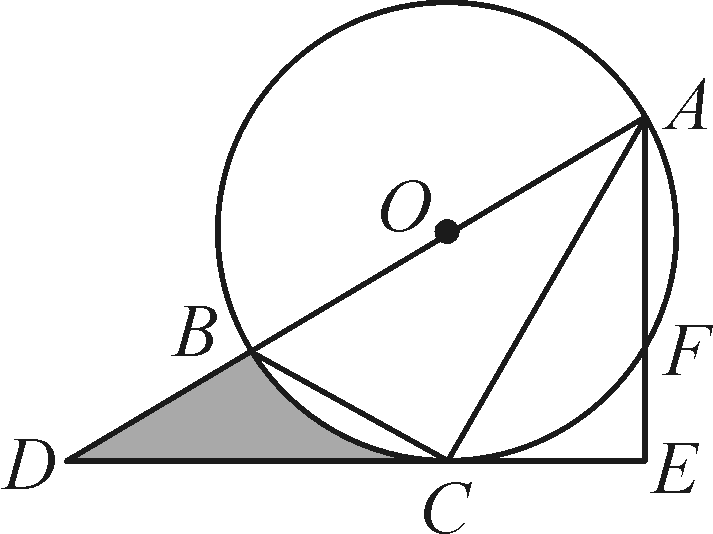
解：(1)连接OC，∵AC平分∠BAE，∴∠BAC＝∠CAE.∵OA＝OC，∴∠OCA＝∠BAC，∴∠OCA＝∠CAE，∴OC∥AE，又AE⊥DC，∴OC⊥DE，∴DE是⊙O的切线

(2)在Rt△AED和Rt△ODC中，∵AE＝6，∠D＝30°，∴AD＝12，OD＝2OC，又OA＝OB＝r，∴OD＝2r，∴2r＋r＝12，解得r＝4，即⊙O的半径是4.∵OC＝4，则OD＝8，CD＝4√3，S阴影＝S△ODC－S扇形OBC＝2(1)×4√3×4－360(60π×42)＝8√3－3(8)π

第175题

(9分)已知四边形ABCD中，AB⊥AD，BC⊥CD，AB＝BC，∠ABC＝120°，∠MBN＝60°，∠MBN绕B点旋转，它的两边分别交AD，DC(或它们的延长线)于E，F.当∠MBN绕点B旋转到AE＝CF时(如图甲)，易证AE＋CF＝EF.当∠MBN绕点B旋转到AE≠CF时，在图乙和图丙这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需要证明．

参考答案：见解析

解析：

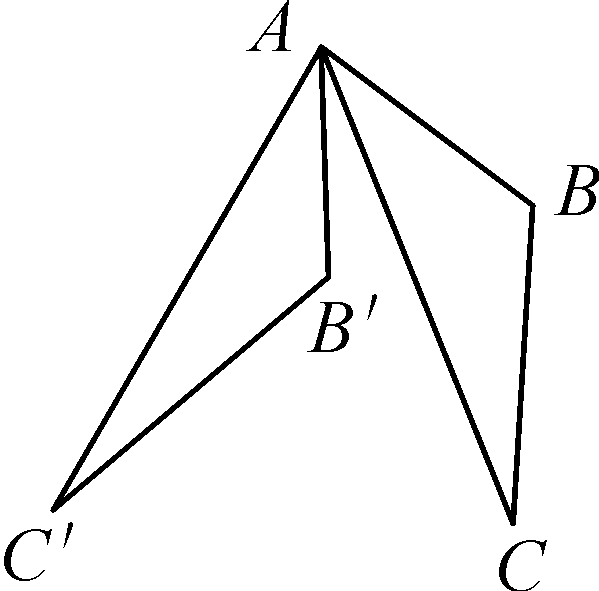
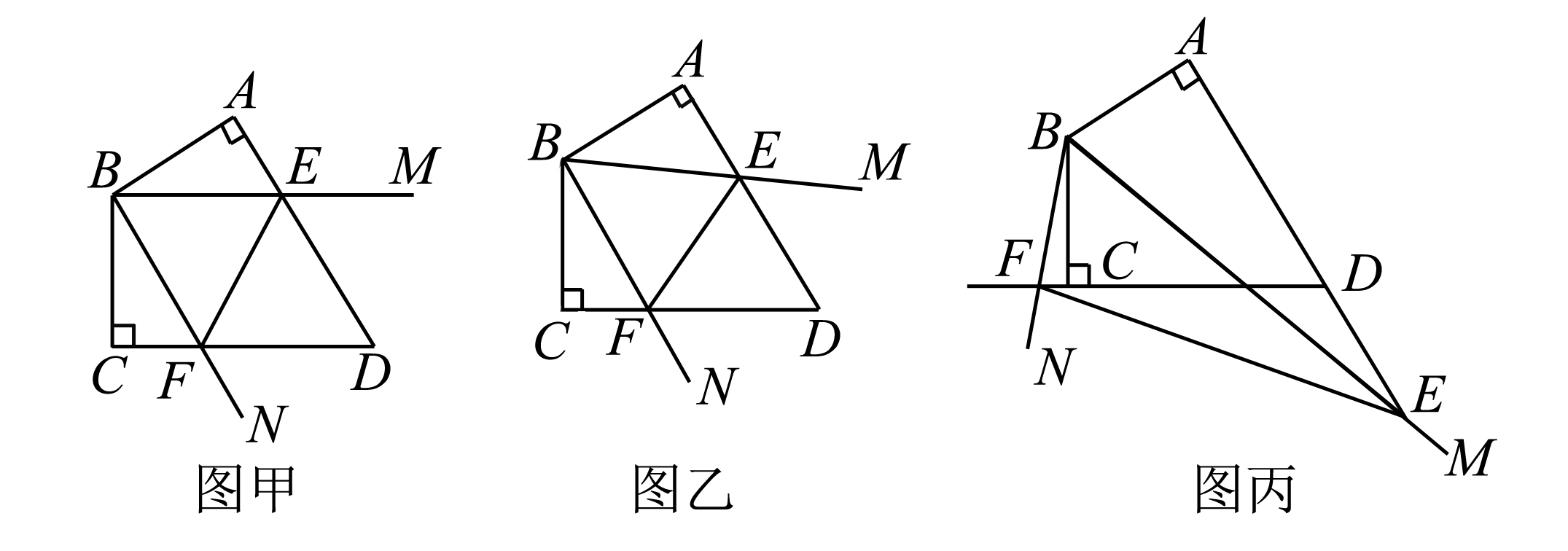
解：对于图乙，将△BAE绕点B顺时针旋转120°到△BCE′，易知∠EBE′＝120°，F，C，E′三点共线，可证△BEF≌△BE′F，可得AE＋CF＝E′C＋CF＝E′F＝EF.对于图丙，类似可以得到AE－CF＝EF

第176题

(12分)如图，已知一条直线过点(0，4)，且与抛物线y＝4(1)x²交于A，B两点，其中点A的横坐标是－2.

(1)求这条直线的解析式及点B的坐标；

参考答案：见解析

解析：

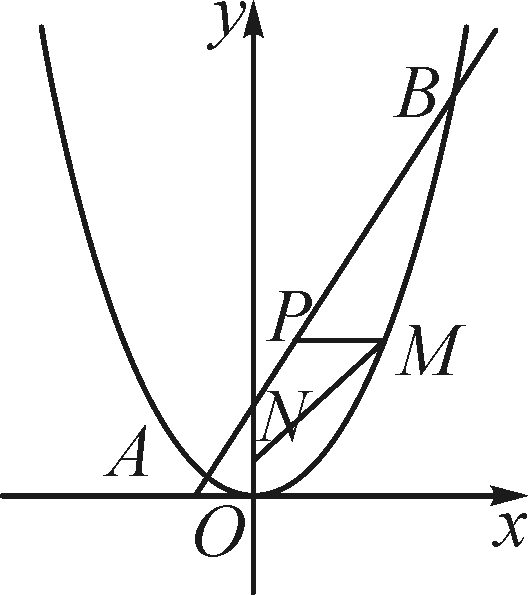
解：(1)y＝2(3)x＋4，B(8，16)

(2)存在．过点B作BG∥x轴，过点A作AG∥y轴，交点为G，∴AG2＋BG2＝AB2，∵由A(－2，1)，B(8，16)可求得AB2＝325.设点C(m，0)，同理可得AC2＝(m＋2)2＋12＝m2＋4m＋5，BC2＝(m－8)2＋162＝m2－16m＋320，①若∠BAC＝90°，则AB2＋AC2＝BC2，即325＋m2＋4m＋5＝m2－16m＋320，解得m＝－2(1)；②若∠ACB＝90°，则AB2＝AC2＋BC2，即325＝m2＋4m＋5＋m2－16m＋320，解得m＝0或m＝6；③若∠ABC＝90°，则AB2＋BC2＝AC2，即m2＋4m＋5＝m2－16m＋320＋325，解得m＝32，∴点C的坐标为(－2(1)，0)，(0，0)，(6，0)，(32，0)

(3)设M(a，4(1)a2)，设MP与y轴交于点Q，在Rt△MQN中，

由勾股定理得MN＝＝4(1)a2＋1，

又∵点P与点M纵坐标相同，

∴2(3)x＋4＝4(1)a2，

∴x＝6(a2－16)，

∴点P的横坐标为6(a2－16)，

∴MP＝a－6(a2－16)，

∴MN＋3MP＝4(1)a2＋1＋3(a－6(a2－16))＝－4(1)a2＋3a＋9＝－14(a－6)2＋18，

∵－2≤6≤8，

∴当a＝6时，取最大值18，

∴当M的横坐标为6时，MN＋3MP的长度的最大值是18

第177题

下面的图形中，既是轴对称图形又是中心对称图形的是(　　)

A.A

B.B

C.C

D.D

参考答案：C

第178题

用配方法解一元二次方程x²－4x＋1＝0时，下列变形正确的为(　　)

A.(x＋2)²＝1

B.(x－2)²＝1

C.(x＋2)²＝3

D.(x－2)²＝3

参考答案：D

第179题

抛物线y＝x²＋4x＋4的对称轴是(　　)

A.直线x＝4

B.直线x＝－4

C.直线x＝2

D.直线x＝－2

参考答案：D

第180题

某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为(　　)

A.48(1－x)²＝36

B.48(1＋x)²＝36

C.36(1－x)²＝48

D.36(1＋x)²＝48

参考答案：D