第121题

（8分） 某中学学生会为考察该校学生参加课外体育活动的情况，采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好（每人只能选其中一项），并将调查结果绘制成如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：

参考答案：见解析

解析：

解：

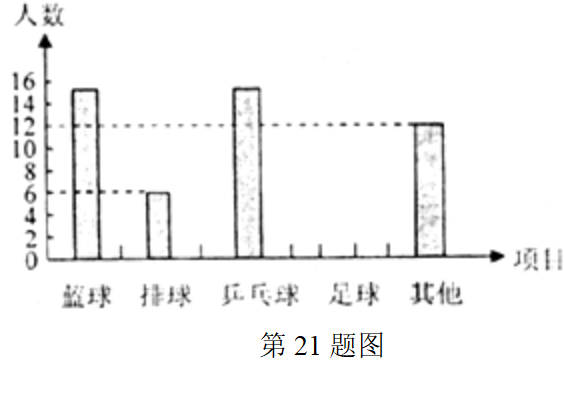
（1）∵，∴这次考察中一共调查了60名学生.

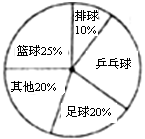
（2）∵1-25%-10%-20%-20%=25%

∴360°×25%=90°

∴在扇形统计图中，“乒乓球”部分所对应的圆心角为90°

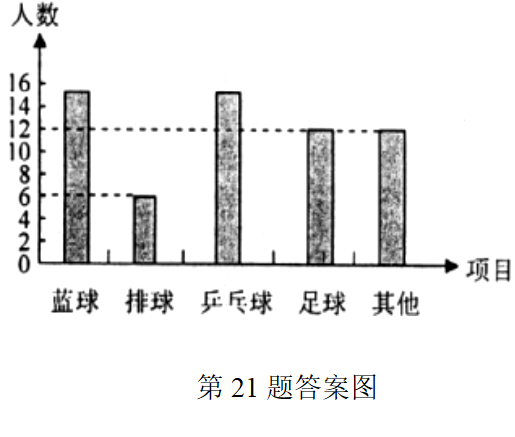
（3）60×20%=12，∴补全统计图如下图

（4）∵1800×25%=450

∴可以估计该校学生喜欢篮球活动的约有450人

第122题

（本题满分8分）如图5的方格纸中ΔABC，的顶点坐标分别为A(-2,5)、B(-4,1) 和C(-1,3)   

（1）作出ΔABC关于x轴对称的ΔA₁B₁C₁，并写出点A、B、C的对称点A₁、B₁、C₁的坐标；

参考答案：见解析

解析：

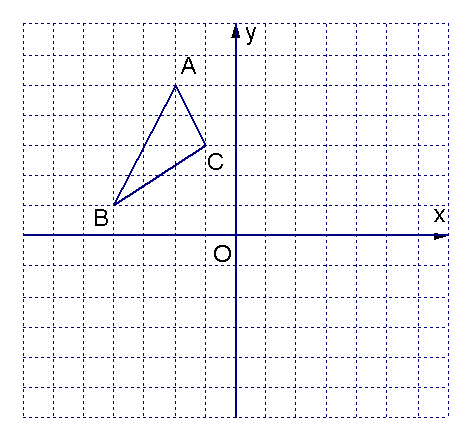
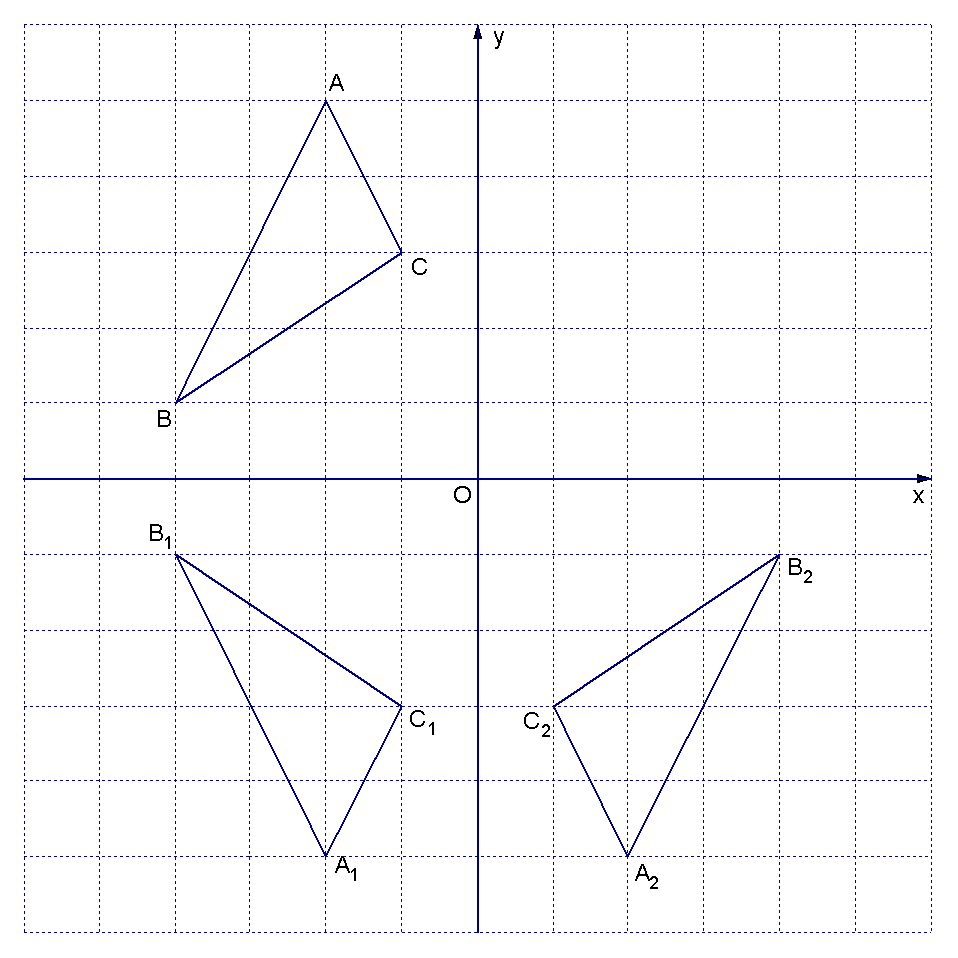
解：（1）ΔA₁B₁C₁如图，A₁(-2,-5)、B₁(-4,-1)、 C₁(-1,-3)

（2）ΔA₂B₂C₂如图，A₂(2,-5)、B₂(4,1)、  C₂ (1,-3)

（3）ΔA₁B₁C₁与ΔA₂B₂C₂关于y轴对称

第123题

如图6，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F.

（1）在图中找出一对全等三角形，并加以证明；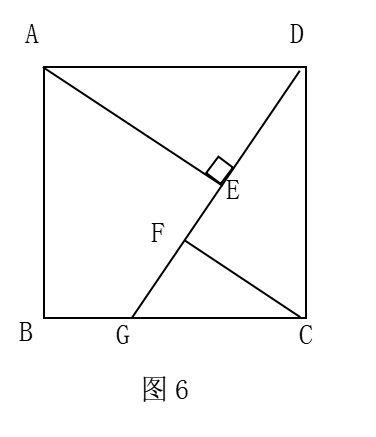

参考答案：见解析

解析：

(1) ΔAED≌ΔDFC.    

∵ 四边形ABCD是正方形,

∴ AD=DC，∠ADC=90º.

又∵ AE⊥DG，CF∥AE，   

∴ ∠AED=∠DFC=90º,…

∴ ∠EAD+∠ADE=∠FDC+∠ADE=90º，

∴ ∠EAD=∠FDC.  

∴ ΔAED≌ΔDFC （AAS）.  

(2) ∵ ΔAED≌ΔDFC，

∴ AE=DF，ED=FC.  …

∵ DF=DE+EF，

∴ AE=FC+EF.

第124题

（13分）如图7，已知二次函数图象的顶点坐标为C(1,0)，直线y=x+m与该二次函数的图象交于A、B两点，其中A点的坐标为(3,4)，B点在轴y上.

（1）求m的值及这个二次函数的关系式；

参考答案：见解析

解析：

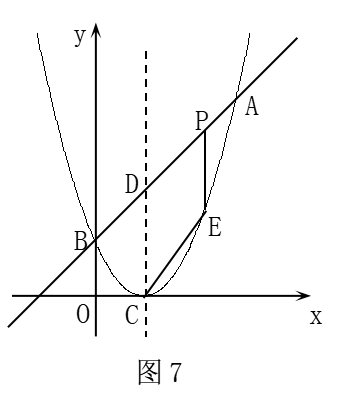
(1) ∵ 点A(3,4)在直线y=x+m上，

∴ 4=3+m.

∴ m=1.   

      设所求二次函数的关系式为y=a(x-1)².

      ∵ 点A(3,4)在二次函数y=a(x-1)²的图象上，

        ∴ 4=a(3-1)²,

        ∴ a=1.

∴ 所求二次函数的关系式为y=(x-1)².

   即y=x²-2x+1.

(2) 设P、E两点的纵坐标分别为y_P和y_E .

∴ PE=h=y_P-y_E

       =(x+1)-(x²-2x+1)  

       =-x²+3x.…

   即h=-x²+3x (0＜x＜3).

第125题

下列图形中既是轴对称图形又是中心对称图形的是(  )

A.A

B.B

C.C

D.D

参考答案：D

第126题

把抛物线y＝x²－1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为(  )

A.y＝(x＋1)²－3  

B.y＝(x－1)²－3

C.y＝(x＋1)²＋1  

D.y＝(x－1)²＋1

参考答案：B

第127题

已知命题“关于x的一元二次方程x²＋bx＋1＝0，必有实数解”是假命题，则在下列选项中，b的值可以是(  )

A.b＝－3

B.b＝－2

C.b＝－1

D.b＝2

参考答案：C

第128题

如图，△ABC内接于⊙O，AB＝BC，∠ABC＝120°，AD为⊙O的直径，AD＝6，那么AB的值为(  )

A.3

B.2√3

C.3 √3

D.2

参考答案：A

第129题

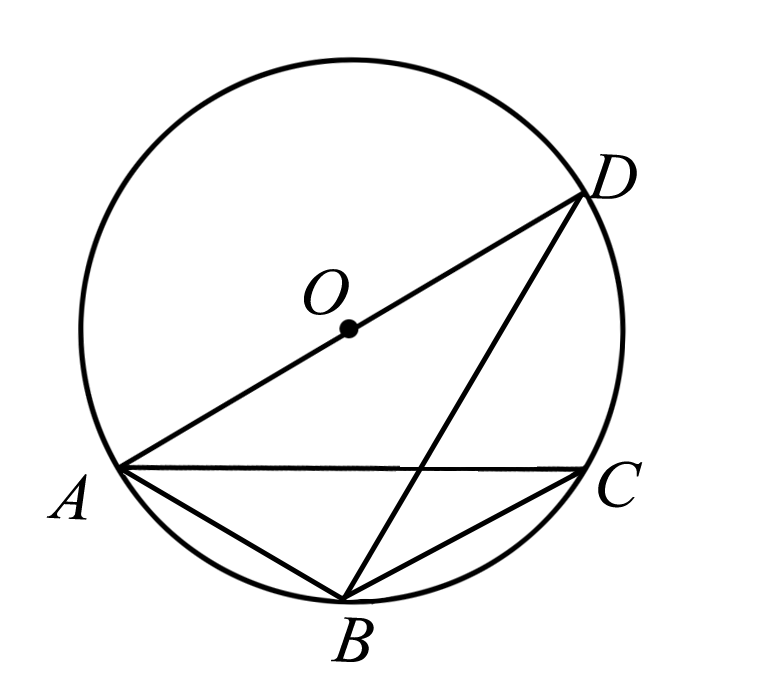
如图，已知AC是⊙O的直径，点B在圆周上(不与A，C重合)，点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB＝3∠ADB，则(  )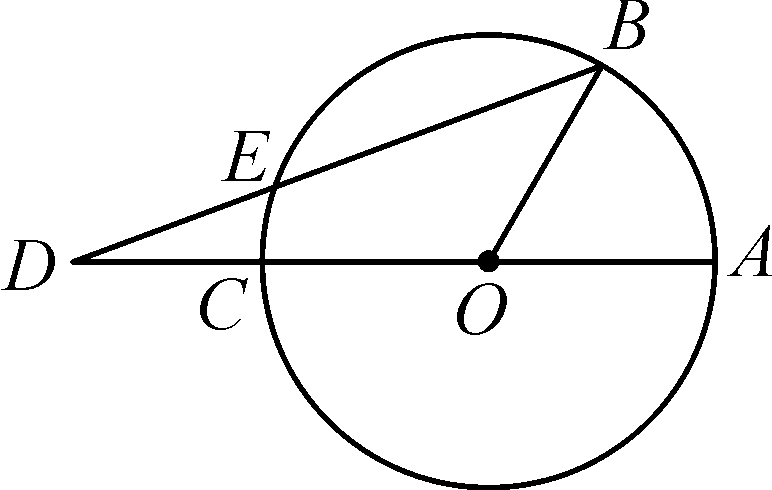

A.DE＝EB  

B.DE＝EB  

C.DE＝DO  

D.DE＝OB

参考答案：D

第130题

如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则的长为(  )

A.π

B.6π

C.3π

D.1.5π

参考答案：D

第131题

二次函数y＝a(x＋m)²＋n的图象如图所示，则一次函数y＝mx＋n的图象经过(  )

A.第一、二、三象限

B.第一、二、四象限

C.第二、三、四象限

D.第一、三、四象限

参考答案：C

第132题

已知a≥2，m²－2am＋2＝0，n²－2an＋2＝0，则(m－1)²＋(n－1)²的最小值是(  )

A.6

B.3

C.－3

D.0

参考答案：A

第133题

如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3，0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为(  )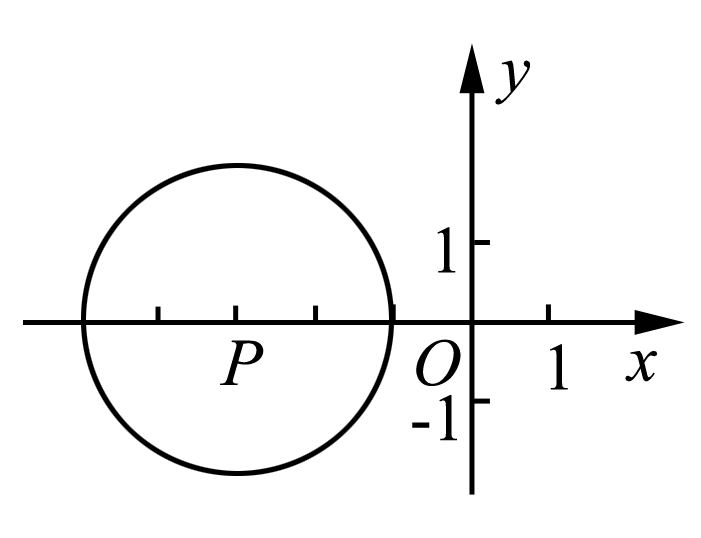

A.1

B.1或5

C.3

D.5

参考答案：B

第134题

如图，二次函数y＝ax²＋bx＋c(a≠0)的图象的顶点在第一象限，且过点(0，1)和(－1，0)．下列结论：①ab＜0；②b²＞4a；③0＜a＋b＋c＜2；④0＜b＜1；⑤当x＞－1时，y＞0.其中正确结论的个数是(  )

A.5个

B.4个

C.3个

D.2个

参考答案：B

第135题

二次函数y＝x²－2x＋6的最小值是____．

参考答案：5

第136题

从－，0，，π，3.5这五个数中，随机抽取一个，则抽到无理数的概率是____．

参考答案：2/5

解析：

第137题

如图，在⊙O中，A，B是圆上的两点，已知∠AOB＝40°，直径CD∥AB，连接AC，则∠BAC＝____度．

参考答案：35

第138题

用等腰直角三角板画∠AOB＝45°，并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°，则三角板的斜边与射线OA的夹角α为____．

参考答案：22°

第139题

如图，顺次连接圆内接矩形各边的中点，得到菱形ABCD，若BD＝10，DF＝4，则菱形ABCD的边长为____．

参考答案：9

第140题

如图，⊙O的半径为2，点A，C在⊙O上，线段BD经过圆心O，∠ABD＝∠CDB＝90°，AB＝1，CD＝，则图中阴影部分的面积为____．

参考答案：5/3 π