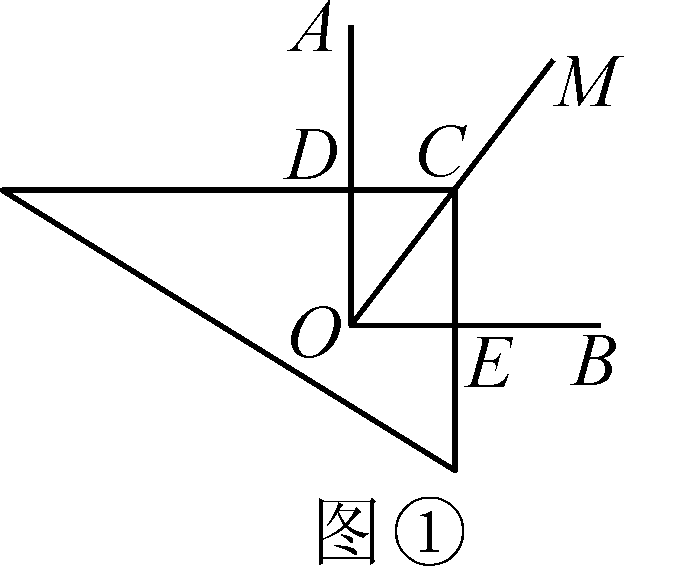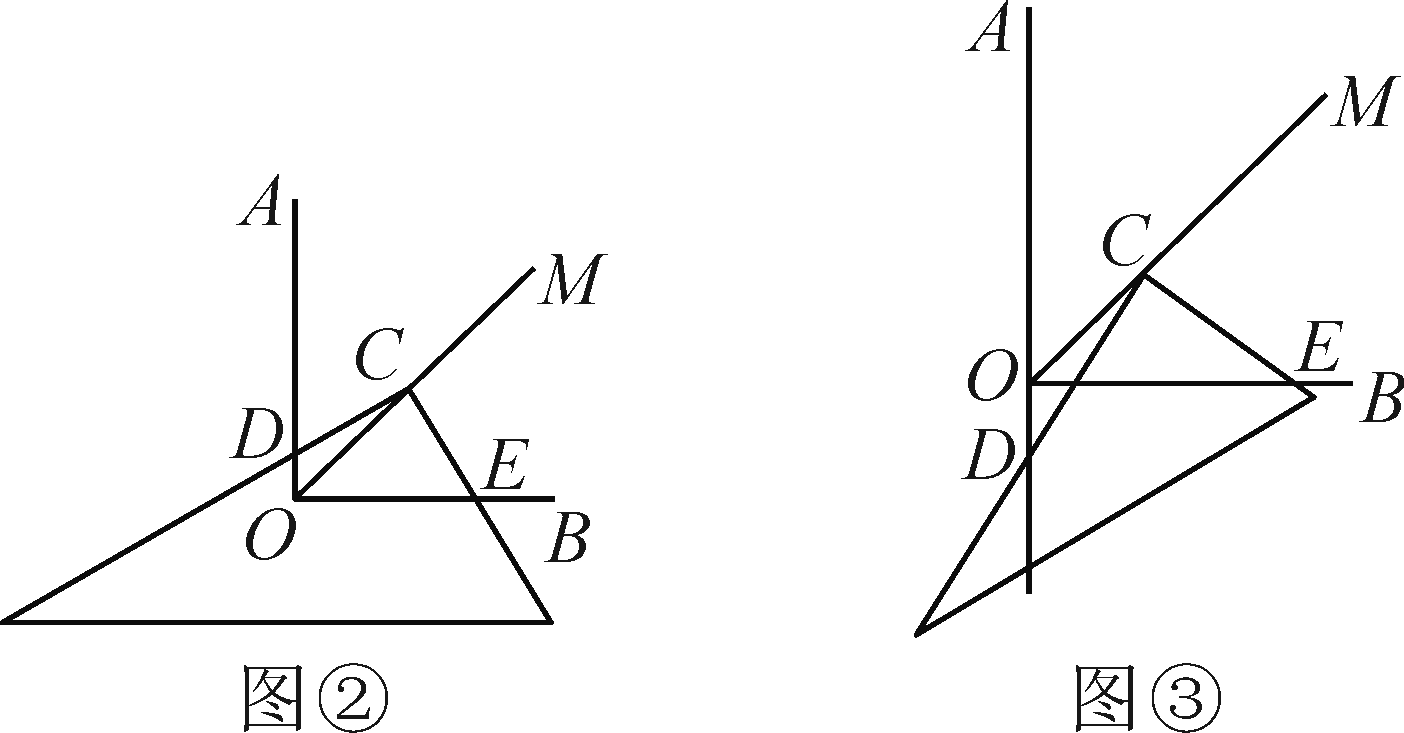第141题

一个底面直径是80 cm，母线长为90 cm的圆锥的侧面展开图的圆心角的度数为____．

参考答案：160°

第142题

已知关于x的二次函数y＝ax²＋bx＋c的图象经过点(－2，y₁)，(－1，y₂)，(1，0)，且y₁＜0＜y₂，对于以下结论：

①abc＞0；

参考答案：②

第143题

(5分)解方程：(x＋1)(x－1)＝2√(2)x.

参考答案：见解析

解析：

解：x₁＝√2＋√3，x₂＝√2－√3

第144题

(7分)设x₁，x₂是关于x的方程x²－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x₁x₂＞x₁＋x₂成立？请说明理由．

参考答案：见解析

解析：

解：不存在．理由：由题意得Δ＝16－4(k＋1)≥0，解得k≤3.∵x₁，x₂是一元二次方程的两个实数根，∴x₁＋x₂＝4，x₁x₂＝k＋1，由x₁x₂＞x₁＋x₂得k＋1＞4，∴k＞3，∴不存在实数k使得x₁x₂＞x₁＋x₂成立

第145题

(8分)如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，2)，B(0，4)，C(0，2)．

(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为(0，－4)，画出平移后对应的△A₂B₂C₂；

参考答案：见解析

解析：

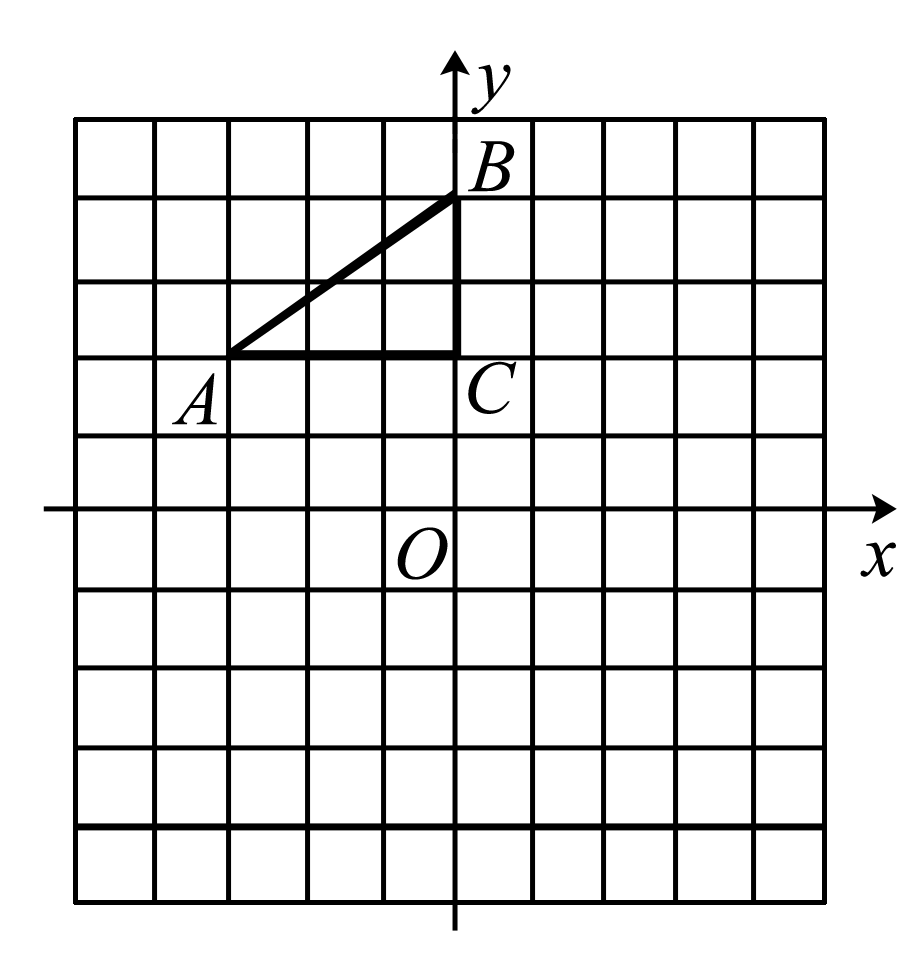
解：(1)图略　(2)旋转中心为(1.5，－1)　(3)P(－2，0)

第146题

小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩．

(1)小明和小刚都在本周日上午去游玩的概率为___；

参考答案：见解析

解析：

解：(1)根据题意，画树状图如图，

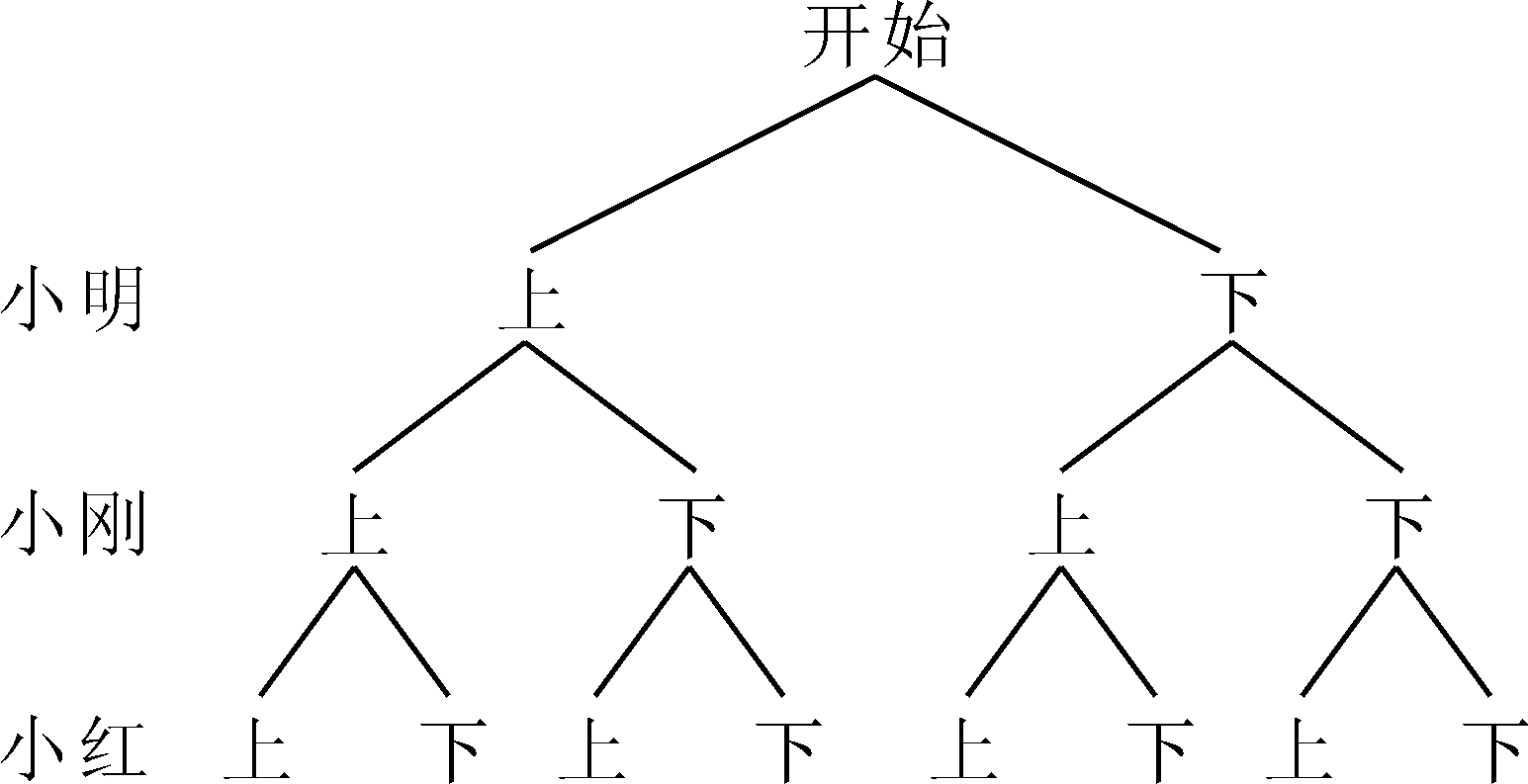
由树状图可知，三人随机选择本周日的上午或下午去游玩共有8种等可能结果，其中小明和小刚都在本周日上午去游玩的结果有(上，上，上)、(上，上，下)2种，∴小明和小刚都在本周日上午去游玩的概率为8(2)＝4(1)　(2)由(1)中树状图可知，他们三人在同一个半天去游玩的结果有(上，上，上)、(下，下，下)这2种，∴他们三人在同一个半天去游玩的概率为8(2)＝4(1)

第147题

(8分)如图，在Rt△ABC中，∠ABC＝90°，以AB为直径作半圆⊙O交AC于点D，点E为BC的中点，连接DE.

(1)求证：DE是半圆⊙O的切线；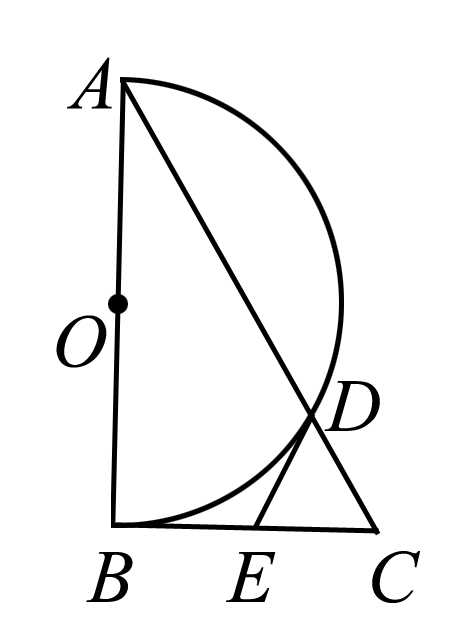

参考答案：见解析

解析：

解：(1)连接OD，OE，BD.∵AB为⊙O的直径，∴∠ADB＝∠BDC＝90°，在Rt△BDC中，E为斜边BC的中点，∴DE＝BE.从而由SSS可证△OBE≌△ODE，∴∠ODE＝∠ABC＝90°，则DE为⊙O的切线　(2)在Rt△ABC中，∠BAC＝30°，∴BC＝2(1)AC.∵BC＝2DE＝4，∴AC＝8.又∵∠C＝60°，DE＝EC，∴△DEC为等边三角形，即DC＝DE＝2，则AD＝AC－DC＝6

第148题

(10分)为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系：y＝－2x＋80.设这种产品每天的销售利润为w元．

(1)求w与x之间的函数关系式；

参考答案：见解析

解析：

解：(1)由题意得w＝(x－20)·y＝(x－20)(－2x＋80)＝－2x²＋120x－1600，故w与x的函数关系式为w＝－2x²＋120x－1600　(2)w＝－2x²＋120x－1600＝－2(x－30)²＋200.

∵－2＜0，

∴当x＝30时，w有最大值，w最大值为200，则该产品销售价定为每千克30元时，每天销售利润最大，最大销售利润为200元　(3)当w＝150时，可得方程－2(x－30)²＋200＝150.解得x₁＝25，x₂＝35.

∵35＞28，

∴x₂＝35不符合题意，应舍去，则该农户想要每天获得150元的销售利润，销售价应定为每千克25元

第149题

(8分)已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E.

当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE＝√(2)OC；

参考答案：见解析

解析：

解：图②中OD＋OE＝√2OC成立．证明：过点C分别作OA，OB的垂线，垂足分别为P，Q.有△CPD≌△CQE，∴DP＝EQ，∵OP＝OD＋DP，OQ＝OE－EQ，又∵OP＋OQ＝√2OC，即OD＋DP＋OE－EQ＝√2OC，∴OD＋OE＝√2OC.图③不成立，有数量关系：OE－OD＝√2OC

第150题

已知m，n是一元二次方程x²＋4x＋3＝0的两个实数根，且|m|＜|n|，抛物线y＝x²＋bx＋c的图象经过点A(m，0)，B(0，n)，如图所示．

(1)求这个抛物线的解析式；

参考答案：见解析

解析：

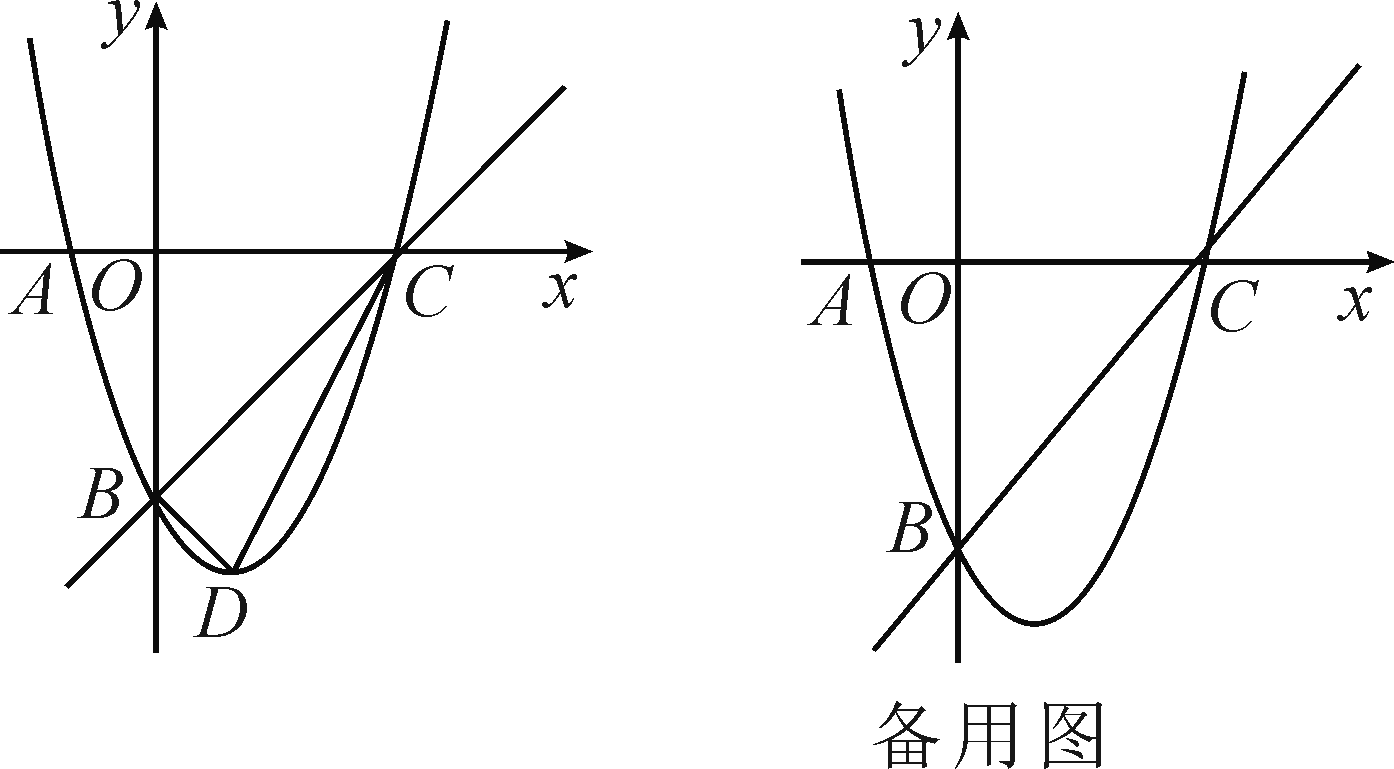
解：(1)y＝x²－2x－3　(2)令y＝0，则x²－2x－3＝0，∴x₁＝－1，x₂＝3，∴C(3，0)，∵y＝x²－2x－3＝(x－1)²－4，∴顶点坐标D(1，－4)，过点D作DE⊥y轴，∵OB＝OC＝3，OE＝4，DE＝1，∴BE＝DE＝1，∴△BOC和△BED都是等腰直角三角形，∴∠OBC＝∠DBE＝45°，∴∠CBD＝90°，∴△BCD是直角三角形

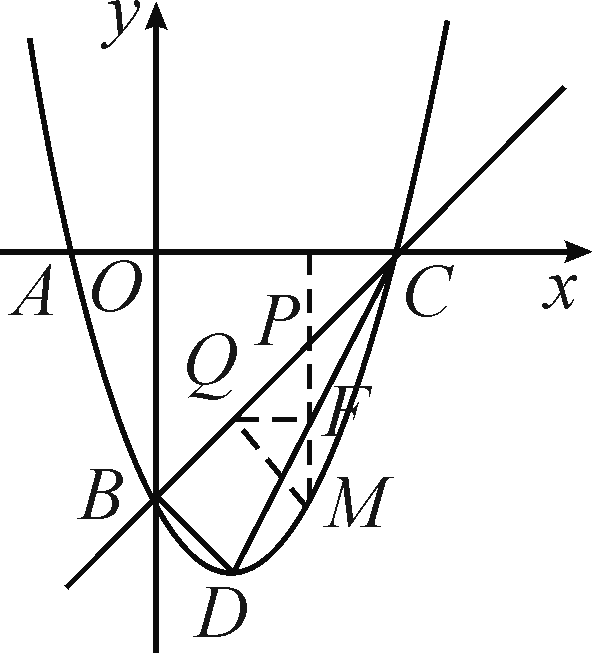
(3)如图，∵B(0，－3)，C(3，0)，∴直线BC的解析式为y＝x－3，∵点P的横坐标为t，PM⊥x轴，∴点M的横坐标为t，∵点P在直线BC上，点M在抛物线上，∴P(t，t－3)，M(t，t²－2t－3)，过点Q作QF⊥PM，∴△PQF是等腰直角三角形，∵PQ＝√2，∴QF＝1，当点P在点M上方时，即0＜t＜3时，PM＝t－3－(t²－2t－3)＝－t²＋3t，∴S＝2(1)PM·QF＝2(1)(－t²＋3t)＝－2(1)t²＋2(3)t；当点P在点M下方时，即t＜0或t＞3时，PM＝t²－2t－3－(t－3)＝t²－3t，∴S＝2(1)PM·QF＝2(1)(t²－3t)＝2(1)t²－2(3)t

第151题

下列图形中，既是轴对称图形又是中心对称图形的是(  )

A.A

B.B

C.C

D.D

参考答案：D

第152题

已知m，n是关于x的一元二次方程x²－3x＋a＝0的两个解，若(m－1)(n－1)＝－6，则a的值为(  )

A.－10

B.4

C.－4

D.10

参考答案：C

第153题

有一种推理游戏叫做“天黑请闭眼”，9位同学参与游戏，通过抽牌决定所扮演的角色，事先做好9张卡牌(除所写文字不同，其余均相同)，其中有法官牌1张，杀手牌2张，好人牌6张．小明参与游戏，如果只随机抽取1张，那么小明抽到好人牌的概率是(  )

A.  

B.

C.  

D.

参考答案：D

第154题

在同一坐标系中，一次函数y＝－mx＋n²与二次函数y＝x²＋m的图象可能是(  )

A.A

B.B

C.C

D.D

参考答案：D

第155题

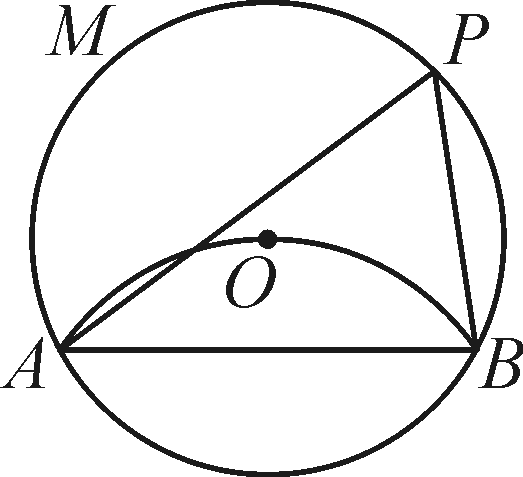
如图，四边形PAOB是扇形OMN的内接矩形，顶点P在MN(︵上，且不与M，N重合，当P点在MN(︵)上移动时，矩形PAOB的形状、大小随之变化，则AB的长度（）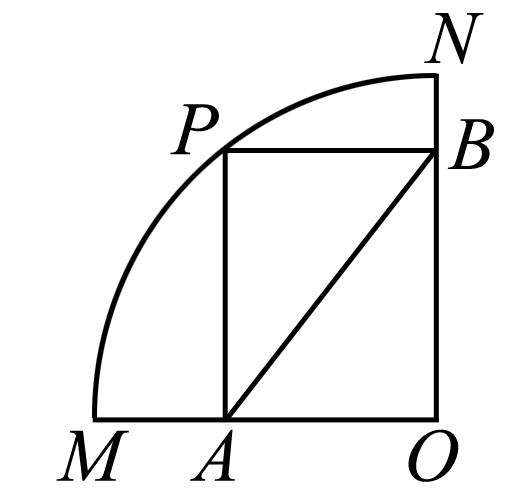

A.变大

B.变小

C.不变

D.不能确定

参考答案：C

第156题

随州市尚市“桃花节”观赏人数逐年增加，据有关部门统计，2014年约为20万人次，2016年约为28.8万人次，设观赏人数年均增长率为x，则下列方程正确的是(  )

A.20(1＋2x)＝28.8

B.28.8(1＋x)²＝20

C.20(1＋x)²＝28.8

D.20＋20(1＋x)＋20(1＋x)²＝28.8

参考答案：C

第157题

如图，在平面直角坐标系中，将△ABC向右平移3个单位长度后得△A₁B₁C₁，再将△A₁B₁C₁绕点O旋转180°后得到△A₂B₂C₂，则下列说法正确的是(  )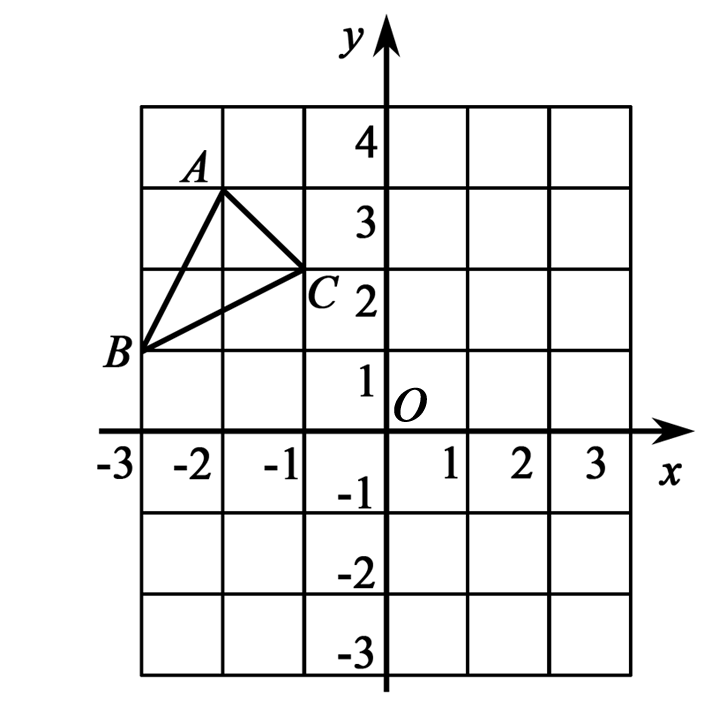

A.A₁的坐标为(3，1)  

B.S四边形ABB₁A₁＝3  

C.B₂C＝2√2 

D.∠AC₂O＝45°

参考答案：D

第158题

如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧AMB(︵)上一点，则∠APB的度数为(  )

A.45°

B.30°

C.75°

D.60°

参考答案：D

第159题 如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是EB(︵)的中点，则下列结论：①OC∥AE；②EC＝BC；③∠DAE＝∠ABE；④AC⊥OE，其中正确的有(  )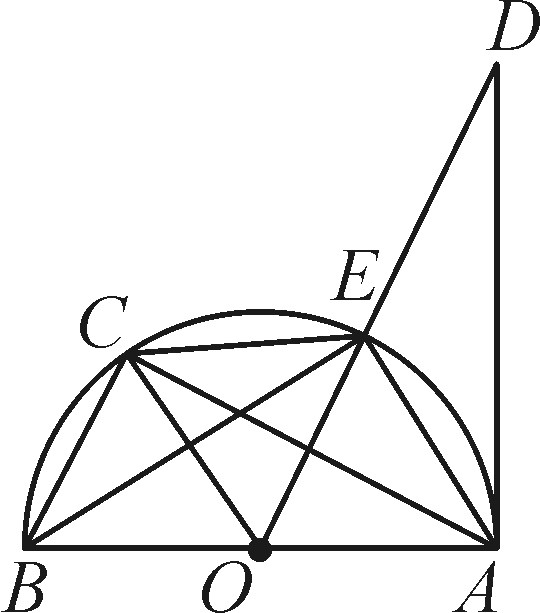

A.1个

B.2个

C.3个

D.4个

参考答案：C

第160题

二次函数y＝a(x－4)²－4(a≠0)的图象在2＜x＜3这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为(  )

A.1

B.－1

C.2

D.－2

参考答案：A