九年级（上）期末数学试卷集（328题）

---

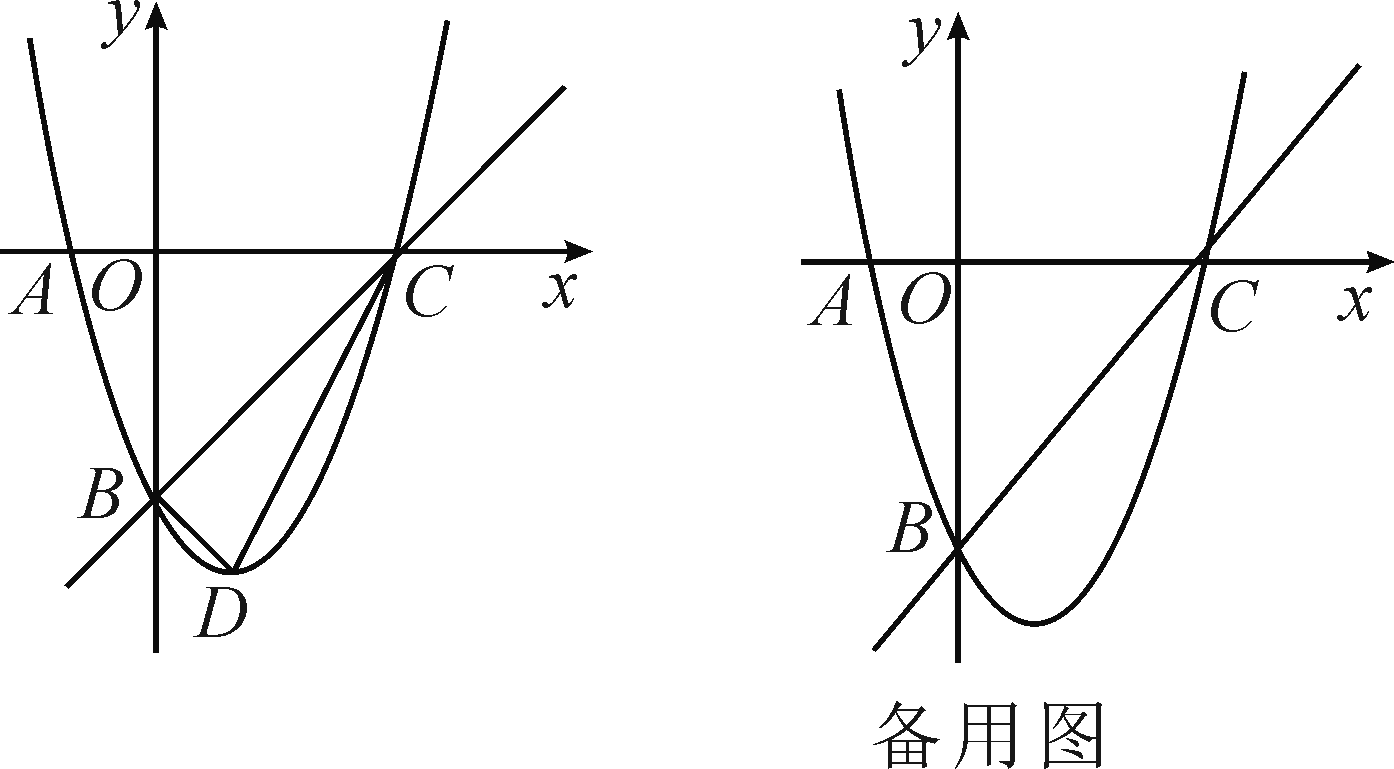
已知m，n是一元二次方程x²＋4x＋3＝0的两个实数根，且|m|＜|n|，抛物线y＝x²＋bx＋c的图象经过点A(m，0)，B(0，n)，如图所示．

(1)求这个抛物线的解析式；

(2)设(1)中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，试求出点C，D的坐标，并判断△BCD的形状；

(3)点P是直线BC上的一个动点(点P不与点B和点C重合)，过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为√2个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

知识点：试卷06

参考答案：见解析

解析：

解：(1)y＝x²－2x－3　(2)令y＝0，则x²－2x－3＝0，∴x₁＝－1，x₂＝3，∴C(3，0)，∵y＝x²－2x－3＝(x－1)²－4，∴顶点坐标D(1，－4)，过点D作DE⊥y轴，∵OB＝OC＝3，OE＝4，DE＝1，∴BE＝DE＝1，∴△BOC和△BED都是等腰直角三角形，∴∠OBC＝∠DBE＝45°，∴∠CBD＝90°，∴△BCD是直角三角形

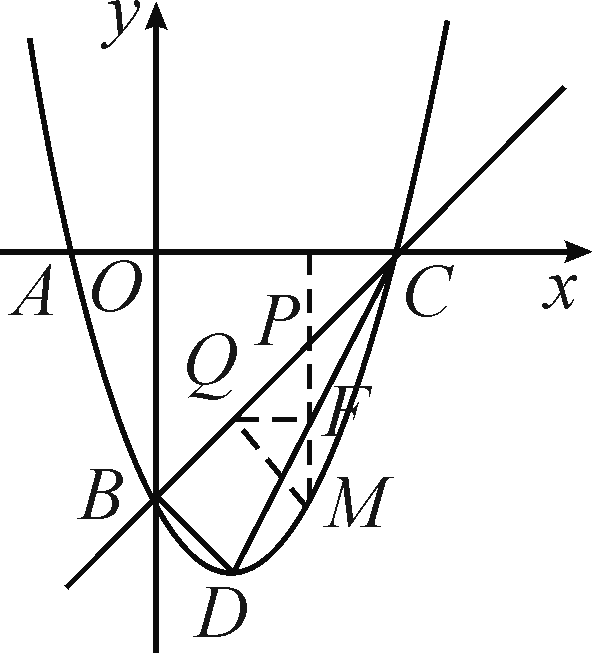
(3)如图，∵B(0，－3)，C(3，0)，∴直线BC的解析式为y＝x－3，∵点P的横坐标为t，PM⊥x轴，∴点M的横坐标为t，∵点P在直线BC上，点M在抛物线上，∴P(t，t－3)，M(t，t²－2t－3)，过点Q作QF⊥PM，∴△PQF是等腰直角三角形，∵PQ＝√2，∴QF＝1，当点P在点M上方时，即0＜t＜3时，PM＝t－3－(t²－2t－3)＝－t²＋3t，∴S＝2(1)PM·QF＝2(1)(－t²＋3t)＝－2(1)t²＋2(3)t；当点P在点M下方时，即t＜0或t＞3时，PM＝t²－2t－3－(t－3)＝t²－3t，∴S＝2(1)PM·QF＝2(1)(t²－3t)＝2(1)t²－2(3)t