第1题

在﹣2，0，2，﹣3这四个数中，最小的数是（　　）

A.2

B.0

C.﹣2

D.﹣3

参考答案：D

解析：

【考点】有理数大小比较．

【专题】计算题．

【分析】根据有理数的大小比较法则（正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小比较即可．

【解答】解：∵﹣3＜﹣2＜0＜2，

∴最小的数是﹣3，

故选D．

【点评】本题考查了有理数的大小比较法则，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．

第2题

如果我们都能改掉餐桌上的陋习，珍惜每一粒粮食，合肥市每年就能避免浪费30.1亿元，将30.1亿用科学记数法表示为（　　）

A.30.1×10⁸

B.3.01×10⁸

C.3.01×10⁹

D.0.301×10¹⁰

参考答案：C

解析：

【考点】科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【解答】解：将30.1亿用科学记数法表示为：3.01×10⁹．

故选：C．

【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

第3题

一元二次方程（x+6）²=16可转化为两个一元一次方程，其中一个一元一次方程是x+6=4，则另一个一元一次方程是（　　）

A.x﹣6=﹣4

B.x﹣6=4

C.x+6=4

D.x+6=﹣4

参考答案：D

解析：

【考点】解一元二次方程-直接开平方法．

【分析】方程两边直接开平方可达到降次的目的，进而可直接得到答案．

【解答】解：（x+6）²=16，

两边直接开平方得：x+6=±4，

则：x+6=4，x+6=﹣4，

故选：D．

【点评】本题主要考查了直接开平方法解一元二次方程，关键是将方程右侧看做一个非负已知数，根据法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”来求解．

第4题

设a=2﹣1，a在两个相邻整数之间，则这两个整数是（　　）

A.1和2

B.2和3

C.3和4

D.4和5

参考答案：B

解析：

【考点】估算无理数的大小．

【分析】先估算出2的大小，再求出a的取值范围即可．

【解答】解：∵2=，9＜12＜16，

∴3＜2＜4，

∴2＜2﹣1＜3，即a在2和3之间．

故选B．

【点评】本题考查的是估算无理数的大小，根据题意估算出2的大小是解答此题的关键．

第5题

直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与∠1互余的角有几个（　　）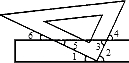

A.2个

B.3个

C.4个

D.6个

参考答案：B

解析：

【考点】余角和补角．

【专题】计算题．

【分析】本题要注意到∠1与∠2互余，并且直尺的两边互相平行，可以考虑平行线的性质．

【解答】解：与∠1互余的角有∠2，∠3，∠4；一共3个．

故选：B．

【点评】正确观察图形，由图形联想到学过的定理是数学学习的一个基本要求．

第6题

某选手在青歌赛中的得分如下（单位：分）：99.60，99.45，99.60，99.70，98.80，99.60，99.83，则这位选手得分的众数和中位数分别是（　　）

A.99.60，99.70

B.99.60，99.60

C.99.60，98.80

D.99.70，99.60

参考答案：B

解析：

【考点】众数；中位数．

【分析】根据众数和中位数的定义求解即可．

【解答】解：数据99.60出现3次，次数最多，所以众数是99.60；

数据按从小到大排列：99.45，99.60，99.60，99.60，99.70，99.80，99.83，中位数是99.60．

故选B．

【点评】本题考查了中位数，众数的意义．找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数．如果数据有奇数个，则正中间的数字即为所求；如果是偶数个，则找中间两位数的平均数．众数是一组数据中出现次数最多的数据，注意众数可以不止一个．

第7题

如图为抛物线y=ax²+bx+c的图象，A、B、C 为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（　　）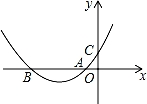

A.ac＜0

B.a﹣b=1

C.a+b=﹣1

D.b＞2a

参考答案：D

解析：

【考点】二次函数图象与系数的关系．

【分析】根据以下知识点分析即可：①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）③常数项c决定抛物线与y轴交点． 抛物线与y轴交于（0，c）．

【解答】解：∵OC=1，

∴c=1，

又∵x=1时，y＞0，

∴a+b+1＞0，

∴a+b＞﹣1，

∴选项A不正确；

∵抛物线开口向上，

∴a＞0；

又∵c=1，

∴ac=a＞0，

∴选项B不正确；

∵OA=1，[来源:学科网ZXXK]

∴x=﹣＜﹣1，

又∵a＞0，

∴b＞2a，

∴选项C不正确；

∵OA=1，

∴x=﹣1时，y=0，

∴a﹣b+c=0，

又∵c=1，

∴a﹣b=﹣1，

∴选项D正确．

故选：D．

【点评】此题主要考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确二次函数各项的系数和图形的关系．

第8题

如图，过▱ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的▱AEMG的面积S₁与▱HCFM的面积S₂的大小关系是（　　）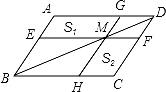

A.S₁＞S₂

B.S₁＜S₂

C.S₁=S₂

D.2S₁=S₂

参考答案：C

解析：

【考点】平行四边形的性质；全等三角形的判定与性质．

【分析】根据平行四边形的性质和判定得出平行四边形GBEP、GPFD，证△ABD≌△CDB，得出△ABD和△CDB的面积相等；同理得出△BEM和△MHB的面积相等，△GMD和△FDM的面积相等，相减即可求出答案．

【解答】解：∵四边形ABCD是平行四边形，EF∥BC，HG∥AB，

∴AD=BC，AB=CD，AB∥GH∥CD，AD∥EF∥BC，

∴四边形HBEM、GMFD是平行四边形，

在△ABD和△CDB中；

∵，

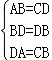∴△ABD≌△CDB（SSS），

即△ABD和△CDB的面积相等；[来源:Zxxk.Com]

同理△BEM和△MHB的面积相等，△GMD和△FDM的面积相等，

故四边形AEMG和四边形HCFM的面积相等，即S₁=S₂．

故选：C．

【点评】本题考查了平行四边形的性质和判定，全等三角形的性质和判定的应用，解此题的关键是求出△ABD和△CDB的面积相等，△BEP和△PGB的面积相等，△HPD和△FDP的面积相等，注意：如果两三角形全等，那么这两个三角形的面积相等

第9题

如果三角形的两条边分别为4和6，那么连结该三角形三边中点所得的周长可能是下列数据中的（　　）

A.6

B.8

C.10

D.12

参考答案：B

解析：

【考点】三角形中位线定理；三角形三边关系．

【分析】本题依据三角形三边关系，可求第三边大于2小于10，原三角形的周长大于12小于20，连接中点的三角形周长是原三角形周长的一半，那么新三角形的周长应大于6而小于10，看哪个符合就可以了．

【解答】解：设三角形的三边分别是a、b、c，令a=4，b=6，

则2＜c＜10，12＜三角形的周长＜20，

故6＜中点三角形周长＜10．

故选B．

【点评】本题重点考查了三角形的中位线定理，利用三角形三边关系，确定原三角形的周长范围是解题的关键．

第10题

附加题：如图，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是（　　）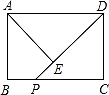

A.

B.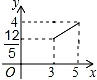

C.

D.

参考答案：C

解析：

【考点】动点问题的函数图象．

【专题】综合题．

【分析】根据实际情况求得自变量的取值范围．

【解答】解：

∵S_△APD=PD×AE=AD×AB，

∴xy=3×4

∴xy=12，

即：y=，为反比例函数，

当P点与C点重合时，x为最小值：x=3，

当P点与B点重合时，x为最大值：x=BD==5，

∴3≤x≤5．

故选：C．

【点评】本题考查了动点问题的函数图象，解决本题的关键是利用面积公式求得函数关系式，特别是要确定自变量的取值范围．

第11题

的平方根是　　．

参考答案：±√3

解析：

【考点】算术平方根；平方根．

【分析】线算出=3，从而得出结论．

【解答】解：∵=3，3的平方根为±，

故答案为：±．

【点评】本题考查了数的平方根，解题的关键是牢记非负数的平方根有两个．

第12题

因式分解：a²b+2ab+b=　　．

参考答案：b（a+1）²

解析：

【考点】提公因式法与公式法的综合运用．

【分析】提取公因式b，剩下的正好是（a+1）的完全平方．

【解答】解：原式=b（a²+2a+1）=b（a+1）²．

故答案为：b（a+1）²．

【点评】本题考查了提取公因式法与公式法的综合运用，先提取公因式b，剩下是（a+1）的完全平方．

第13题

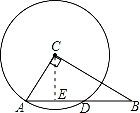
如图，在直角三角形ABC中，∠ACB=90°，AC=1，BC=2，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为　　．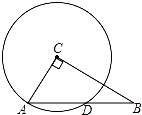

参考答案：

解析：

【考点】垂径定理；勾股定理．

【分析】作CE⊥AB于E，根据勾股定理得到AB=，利用三角形面积公式求出CE，根据勾股定理求出AE，根据垂径定理计算即可．

【解答】解：作CE⊥AB于E，

则AE=AD，

∵∠ACB=90°，AC=1，BC=2，

∴AB==，

×AB×CE=AC×BC，即×CE=，

解得，CE=，

AE==，

则AD=2AE=，

故答案为：．

【点评】本题考查的是勾股定理和垂径定理的应用，垂径定理：垂直弦的直径平分这条弦，并且平分弦所对的两条弧．

第14题

如图，等腰直角△ABC腰长为a，现分别按图1，图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ．设△ABC的面积为S，正方形ADFE的面积为S₁，正方形PMNQ的面积为S₂．①AD：AB=1：2；②AP：AB=1：3；③S₁+S₂＞S；④设在△ABC内任意截取一个正方形的面积为S₃，则S₃≤S₁．上述结论中正确的是　　．

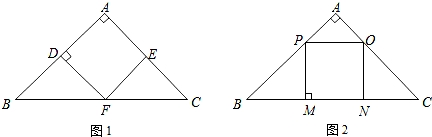
参考答案：①②④

解析：

【考点】相似三角形的判定与性质；等腰直角三角形；正方形的性质．

【分析】①如图1：根据等腰三角形的性质求解；

②图2：同图1的证法；

③由（1）得出的AB、AD、AP、AB的关系，然后用a表示出AB、AD、AP的值，这样就能表示出S₁、S₂和S，然后进行比较即可；

④结合③，即可求得答案．

【解答】解：①图1中，∵△ABC是等腰直角三角形，四边形ADFE是正方形，

∴AD=DF，∠B=45°，

∴DF=DB，

∴AD=DB，

∴AD：AB=1：2；故正确；

②图2中，同理：PM=MN，∠B=45°，

∴PM=MB，

∴MN=MB，

∴MN=MB=NC，

∴AP：AB=PQ：BC=MN：BC=1：3；故正确；

③图1中，S₁=（a）²=a²，

∵PQ：BC=AP：AB=1：3，

∴PQ=a，

∴S₂=（a）²=a²，

∴S₁+S₂=（+）a²=a²，

∵S=a²=a²，

∴S₁+S₂＜S；故错误；

④由③可得：在△ABC内任意截取一个正方形的面积为S₃，则S₃≤S₁；故正确．

故答案为：①②④．

【点评】此题考查了相似三角形的判定与性质以及等腰直角三角形的性质．注意掌握面积的求解方法是关键．

第15题

请从下列三个代数式中任选两个（一个作为分子，一个作为分母）构造一个分式，并化简该分式．a²﹣1，a²﹣1，a²﹣2a+1，然后请你自选一个合理的数代入求值．

参考答案：见解析

解析：

【考点】分式的化简求值．

【专题】开放型．

【分析】根据分式的定义即可构造一个分式，然后取一个使得分式有意义的值代入即可．

【解答】解： ==，

当a=2时，原式==3．

或=，

当a=2时，原式==．

【点评】本题考查分式的定义，分式的约分，理解题意是解题的关键，取值时注意使得分式有意义．

第16题

如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

（1）画出△ABC关于x轴对称的△A₁B₁C₁，并写出点A₁的坐标．

参考答案：见解析

解析：

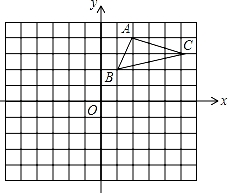
【考点】作图-旋转变换；作图-轴对称变换．

【分析】（1）分别找出A、B、C三点关于x轴的对称点，再顺次连接，然后根据图形写出A点坐标；

（2）将△A₁B₁C₁中的各点A₁、B₁、C₁绕原点O旋转180°后，得到相应的对应点A₂、B₂、C₂，连接各对应点即得△A₂B₂C₂．

【解答】解：（1）如图所示：点A₁的坐标（2，﹣4）；

（2）如图所示，点A₂的坐标（﹣2，4）．

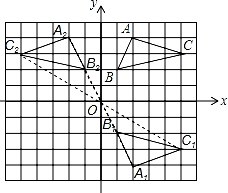
【点评】本题考查图形的轴对称变换及旋转变换．解答此类题目的关键是掌握旋转的特点，然后根据题意找到各点的对应点，然后顺次连接即可．

第17题

2014年3月8日凌晨，马来西亚航空公司一架航班号为MH370的波音777客机于凌晨零点左右从吉隆坡飞往北京，计划6：30抵达北京首都国际机场，却在凌晨1：30分失去联系．已知该飞机起飞时油箱内存有15000升油，起飞后一直保持速度为400km/h匀速直线运动，且每千米的耗油量为5升，请用不等式的知识求出该飞机在失去联系后能最多航行多少千米？

参考答案：见解析

解析：

【考点】一元一次不等式的应用．

【分析】根据飞机的耗油量得出它飞行的最大距离，进而得出的不等式求出答案．

【解答】解：设该飞机在失去联系后能航行x千米，

1：30﹣0：00=1.5（小时），

由题意得：1.5×400×5+5x≤15000

解得：x≤2400．

答：该飞机在失去联系后最多能航行2400千米．

【点评】此题主要考查了一元一次不等式的应用，根据题意结合飞机飞行的距离得出正确不等关系是解题关键．

第18题

如图，矩形ABCD中，AB=6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A₁B₁C₁D₁，第2次平移将矩形A₁B₁C₁D₁沿A₁B₁的方向向右平移5个单位，得到矩形A₂B₂C₂D₂…，第n次平移将矩形A_n﹣1B_n﹣1C_n﹣1D_n﹣1沿A_n﹣1B_n﹣1的方向平移5个单位，得到矩形A_nB_nC_nD_n（n＞2）．

参考答案：见解析

解析：

【考点】平移的性质；一元一次方程的应用；矩形的性质．

【专题】规律型．

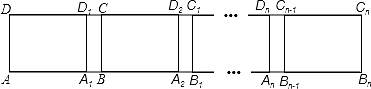
【分析】（1）根据平移的性质得出AA₁=5，A₁A₂=5，A₂B₁=A₁B₁﹣A₁A₂=6﹣5=1，进而求出AB₁和AB₂的长；

（2）根据（1）中所求得出数字变化规律，进而得出AB_n=（n+1）×5+1求出n即可．

【解答】解：（1）∵AB=6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A₁B₁C₁D₁，

第2次平移将矩形A₁B₁C₁D₁沿A₁B₁的方向向右平移5个单位，得到矩形A₂B₂C₂D₂…，

∴AA₁=5，A₁A₂=5，A₂B₁=A₁B₁﹣A₁A₂=6﹣5=1，

∴AB₁=AA₁+A₁A₂+A₂B₁=5+5+1=11，

∴AB₂的长为：5+5+6=16；

（2）∵AB₁=2×5+1=11，AB₂=3×5+1=16，

∴AB_n=（n+1）×5+1=56，

解得：n=10．

【点评】此题主要考查了平移的性质以及一元一次方程的应用，根据平移的性质得出AA₁=5，A₁A₂=5是解题关键．

第19题

一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α （∠CBE=α，如图所示）．

探究 如图1，液面刚好过棱CD，并与棱BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．解决问题：

参考答案：见解析

解析：

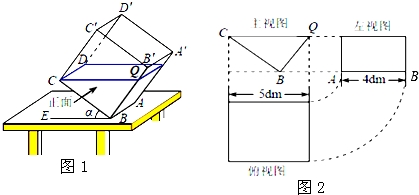
【考点】解直角三角形的应用．

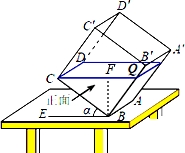
【分析】（1）根据水面与水平面平行可以得到CQ与BE平行，利用勾股定理即可求得BQ的长；

（2）液体正好是一个以△BCQ是底面的直棱柱，据此即可求得液体的体积；

（3）求出∠BCQ的正切值即可得到其度数．

【解答】解：（1）CQ∥BE，BQ==3dm；

故答案为：平行，3；

（2）V_液=×3×4×4=24（dm³）；

（3）过点B作BF⊥CQ，垂足为F，

∵×3×4=×5×BF，

∴BF=，

∴液面到桌面的高度；

∵在Rt△BCQ中，tan∠BCQ=，

∴α=∠BCQ=37°．

【点评】本题考查了解直角三角形的应用，熟练掌握四边形的体积计算以及对三视图的认识，正确理解棱柱的体积的计算是关键．

第20题

面对即将到来的五一小长假，胡老师一家计划用两天时间参观岱山湖、紫蓬山森林公园、滨湖湿地公园、三国遗址公园四个景区中的两个；第一天从4个景区中随机选择一个，第二天从余下3个景区中再随机选择一个，如果每个景区被选中的机会均等．

（1）请画树状图或表格的方法表示出所有可能出现的结果；

参考答案：见解析

解析：

【考点】列表法与树状图法．

【专题】计算题．

【分析】（1）用A、B、C、D分别表示岱山湖、紫蓬山森林公园、滨湖湿地公园、三国遗址公园四个景区，然后画树状图展示所有12种等可能的结果数；

（2）在12种等可能的结果中找出滨湖湿地公园被选中的结果数，然后根据概率公式求解．

【解答】解：（1）用A、B、C、D分别表示岱山湖、紫蓬山森林公园、滨湖湿地公园、三国遗址公园四个景区，

画树状图为：

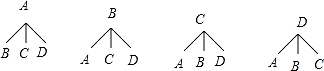
共有12种等可能的结果数；

（2）滨湖湿地公园被选中的结果数为6，

所以滨湖湿地公园被选中的概率==．

【点评】本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．