九年级（上）期末数学试卷集（328题）

---

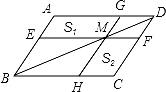
如图，过▱ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的▱AEMG的面积S₁与▱HCFM的面积S₂的大小关系是（　　）

A.S₁＞S₂

B.S₁＜S₂

C.S₁=S₂

D.2S₁=S₂

知识点：试卷01

参考答案：C

解析：

【考点】平行四边形的性质；全等三角形的判定与性质．

【分析】根据平行四边形的性质和判定得出平行四边形GBEP、GPFD，证△ABD≌△CDB，得出△ABD和△CDB的面积相等；同理得出△BEM和△MHB的面积相等，△GMD和△FDM的面积相等，相减即可求出答案．

【解答】解：∵四边形ABCD是平行四边形，EF∥BC，HG∥AB，

∴AD=BC，AB=CD，AB∥GH∥CD，AD∥EF∥BC，

∴四边形HBEM、GMFD是平行四边形，

在△ABD和△CDB中；

∵，

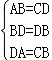∴△ABD≌△CDB（SSS），

即△ABD和△CDB的面积相等；[来源:Zxxk.Com]

同理△BEM和△MHB的面积相等，△GMD和△FDM的面积相等，

故四边形AEMG和四边形HCFM的面积相等，即S₁=S₂．

故选：C．

 

【点评】本题考查了平行四边形的性质和判定，全等三角形的性质和判定的应用，解此题的关键是求出△ABD和△CDB的面积相等，△BEP和△PGB的面积相等，△HPD和△FDP的面积相等，注意：如果两三角形全等，那么这两个三角形的面积相等