九年级（上）期末数学试卷集（328题）

---

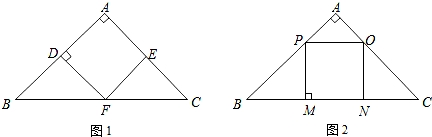
如图，等腰直角△ABC腰长为a，现分别按图1，图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ．设△ABC的面积为S，正方形ADFE的面积为S₁，正方形PMNQ的面积为S₂．①AD：AB=1：2；②AP：AB=1：3；③S₁+S₂＞S；④设在△ABC内任意截取一个正方形的面积为S₃，则S₃≤S₁．上述结论中正确的是　　．

 

知识点：试卷01

参考答案：①②④

解析：

【考点】相似三角形的判定与性质；等腰直角三角形；正方形的性质．

【分析】①如图1：根据等腰三角形的性质求解；

②图2：同图1的证法；

③由（1）得出的AB、AD、AP、AB的关系，然后用a表示出AB、AD、AP的值，这样就能表示出S₁、S₂和S，然后进行比较即可；

④结合③，即可求得答案．

【解答】解：①图1中，∵△ABC是等腰直角三角形，四边形ADFE是正方形，

∴AD=DF，∠B=45°，

∴DF=DB，

∴AD=DB，

∴AD：AB=1：2；故正确；

②图2中，同理：PM=MN，∠B=45°，

∴PM=MB，

∴MN=MB，

∴MN=MB=NC，

∴AP：AB=PQ：BC=MN：BC=1：3；故正确；

③图1中，S₁=（a）²=a²，

∵PQ：BC=AP：AB=1：3，

∴PQ=a，

∴S₂=（a）²=a²，

∴S₁+S₂=（+）a²=a²，

∵S=a²=a²，

∴S₁+S₂＜S；故错误；

④由③可得：在△ABC内任意截取一个正方形的面积为S₃，则S₃≤S₁；故正确．

故答案为：①②④．

【点评】此题考查了相似三角形的判定与性质以及等腰直角三角形的性质．注意掌握面积的求解方法是关键．