第41题

已知，如图，在△ABC中，点D在AB边上，连接CD，∠1=∠2．

（1）求证：△ACD∽△ABC；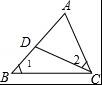

参考答案：见解析

解析：

【考点】相似三角形的判定与性质．

【分析】（1）根据相似三角形的判定定理即可得到结论；

（2）根据相似三角形的性质得到，代入数据即可得到结果．

【解答】（1）证明：∵∠1=∠2，∠A=∠A，

∴△ACD∽△ABC；

（2）解：∵△ACD∽△ABC，

∴，

∴AC²=AB•AD，

∵AD=2，BD=1，

∴AB=3，

∴AC=．

第42题

学校旁边的文具店里有A、B、C、D四种笔记本，每种笔记本数量充足，某同学去该店购买笔记本，每种笔记本被选中的可能性相同．

（1）若他去买一本笔记本，则他买到A种笔记本的概率是　　；

参考答案：见解析

解析：

【考点】列表法与树状图法；概率公式．

【分析】（1）由学校旁边的文具店里有A、B、C、D四种笔记本，直接利用概率公式求解即可求得答案；

（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好买到A种笔记本和C种笔记本的情况，再利用概率公式即可求得答案．

【解答】解：（1）∵学校旁边的文具店里有A、B、C、D四种笔记本，

∴若他去买一本笔记本，则他买到A种笔记本的概率是：；

故答案为：．

（2）画树状图得：

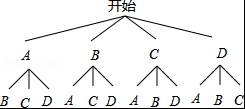
∵共有12种等可能的结果，恰好买到A种笔记本和C种笔记本的有2种情况，

∴恰好买到A种笔记本和C种笔记本的概率为： =．

第43题

已知，如图，△ABC中，CD平分∠ACB，DE∥BC，AD：DB=7：5，AC=24，求DE的长．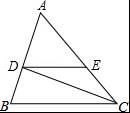

参考答案：见解析

解析：

【考点】相似三角形的判定与性质．

【分析】根据平行线分线段成比例的知识求出AE，EC，然后判断ED=EC，即可得出答案．

【解答】解：∵DE∥BC，

∴，

又∵AC=24，

∴AE=14，EC=10，

∵CD平分∠ACB交AB于D，

∴∠ACD=∠DCB，

又∵DE∥BC，

∴∠EDC=∠DCB，

∴∠ACD=∠EDC，

∴DE=EC=10．

第44题

已知：y=2x²﹣ax﹣a²，且当x=1时，y=0，先化简，再求值：（1﹣）÷．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】先根据分式混合运算的法则把原式进行化简，再由当x=1时，y=0求出a的值，选取合适的a的值代入进行计算即可．

【解答】解：原式=[1﹣]÷

=•

=，

∵y=2x²﹣ax﹣a²，且当x=1时，y=0，

∴2﹣a﹣a²=0，解得a₁=1，a₂=﹣2，

当a=1时，原式=3；

当a=﹣2时，a+2=0，原式无意义．

故原式=3．

第45题

如图，一艘渔船位于小岛M的北偏东42°方向、距离小岛180海里的A处，渔船从A处沿正南方向航行一段距离后，到达位于小岛南偏东60°方向的B处．

（1）求渔船从A到B的航行过程中与小岛M之间的最小距离（参考数据：参考数据：sin42°≈0.6691，cos42°≈0.7431，tan42°≈0.9044，≈1.732，结果精确到0.1海里）

参考答案：见解析

解析：

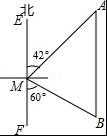
【考点】解直角三角形的应用-方向角问题．

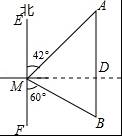
【分析】（1）过点M作MD⊥AB于点D，根据∠AME的度数求出∠A=42°，再根据AM的值求出和特殊角的三角函数值即可求出答案；

（2）在Rt△DMB中，根据∠BMF=60°，得出∠DMB=30°，再根据MD的值求出MB的值，最后根据路程÷速度=时间，即可得出答案．

【解答】解：（1）过点M作MD⊥AB于点D，

∵∠AME=42°，

∴∠A=42°，

∵AM=180海里，

∴MD=AM•sin42°≈120.4（海里），

答：渔船从A到B的航行过程中与小岛M之间的最小距离约为120.4海里；

（2）在Rt△DMB中，

∵∠BMF=60°，

∴∠DMB=30°，

∵MD=120.4海里，

∴MB=≈139，0，

∴139.0÷20≈7.0（小时），

答：渔船从B到达小岛M的航行时间约为7.0小时．

第46题

如图，直线y=x﹣1与反比例函数y=的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．

（1）求反比例函数的解析式；

参考答案：见解析

解析：

【考点】反比例函数与一次函数的交点问题．

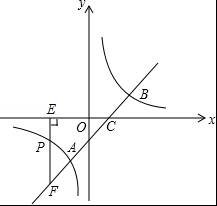
【分析】（1）将点A的坐标代入直线解析式求出m的值，再将点A的坐标代入反比例函数解析式可求出k的值，继而得出反比例函数关系式；

（2）将点P的纵坐标代入反比例函数解析式可求出点P的横坐标，将点P的横坐标和点F的横坐标相等，将点F的横坐标代入直线解析式可求出点F的纵坐标，将点的坐标转换为线段的长度后，即可计算△CEF的面积．

【解答】解：（1）将点A的坐标代入y=x﹣1，可得：m=﹣1﹣1=﹣2，

将点A（﹣1，﹣2）代入反比例函数y=，可得：k=﹣1×（﹣2）=2，

故反比例函数解析式为：y=．

（2）将点P的纵坐标y=﹣1，代入反比例函数关系式可得：x=﹣2，

将点F的横坐标x=﹣2代入直线解析式可得：y=﹣3，

故可得EF=3，CE=OE+OC=2+1=3，

故可得S_△CEF=CE×EF=．

第47题

通过市场调查，一段时间内某地区某一种农副产品的需求数量y（千克）与市场价格x（元/千克）（0＜x＜30）存在下列关系：

参考答案：见解析

解析：

【考点】一次函数的应用．

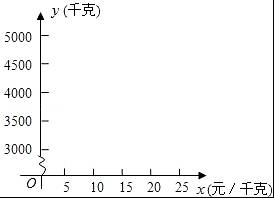
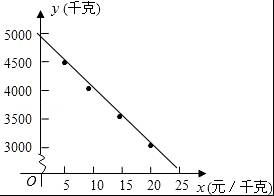
【分析】（1）通过描点画图可知y是x的一次函数，从而利用待定系数法即可求出该解析式；

（2）令y=z，求出此时的x，则农民的总销售收入是xy元；

（3）可设这时该农副产品的市场价格为a元/千克，因为该地区农民的总销售收入比未精加工市场平衡时增加了17600元，则a（﹣100a+5000）=40000+17600，解之即可．

【解答】解：（1）描点．

因为由图象可知，y是x的一次函数，

所以设y=kx+b，

由x=5，y=4500；x=10，y=4000得：

则

所以

即y=﹣100x+5000

（2）∵y=z，

∴﹣100x+5000=400x，

∴x=10．

∴总销售收入=10×4000=40000（元）

∴农副产品的市场价格是10元/千克，农民的总销售收入是40000元．

（3）设这时该农副产品的市场价格为a元/千克，则

a（﹣100a+5000）=40000+17600，

解之得：a₁=18，a₂=32．

∵0＜a＜30，

∴a=18．

∴这时该农副产品的市场价格为18元/千克．

第48题

如图①所示，矩形ABCD一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的点P处，折痕与边BC交于点O，连接AP，OP，OA，△PDA的面积是△OCP的面积的4倍．

参考答案：见解析

解析：

【考点】相似形综合题．

【分析】（1）利用折叠和矩形的性质可得到∠C=∠D，∠APD=∠POC，可证得相似；

（2）利用面积比可求得PC的长，在Rt△APD中利用勾股定理可求得AB的长；

（3）①结合描述画出图形即可，②作MQ∥AN交PB于点Q，利用条件证明△MFQ≌△NFB，得到EF=PB，且可求出PB的长，可得出结论．

【解答】（1）证明：∵四边形ABCD是矩形，

∴AD=BC，DC=AB，∠DAB=∠B=∠C=∠D=90°，

由折叠可得：AP=AB，PO=BO，∠PAO=∠BAO，∠APO=∠B，

∴∠APO=90°，

∴∠APD=90°﹣∠CPO=∠POC，

∴△OCP∽△PDA；

（2）解：∵△OCP与△PDA的面积比为1：4，

∴==，

∴CP=4，

设AB=x，则AP=x，DP=x﹣4，

在Rt△ADP中，由勾股定理可得AP²=AD²+DP²，

即x²=8²+（x﹣4）²，解得x=10，

即边AB的长为10；

（3）解：①如图所示，

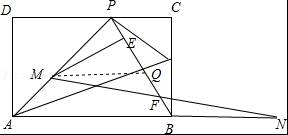
②EF的长度不变，理由如下：

作MQ∥AN，交PB于点Q，如上图，

∵AP=AB，MQ∥AN，

∴∠APB=∠ABP，∠ABP=∠MQP，

∴∠∠APB=∠MQP，

∴MP=MQ，

∵ME⊥PQ，

∴PE=EQ=PQ，

∵BN=PN，MP=MQ，

∴BN=QM，

∵MQ∥AN，

∴∠QMF=∠BNF，

在△MFQ和△NFB中，

，

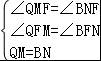∴△MFQ≌△NFB（AAS），

∴QF=BF，

∴QF=QB，

∴EF=EQ+QF=PQ+QB=PB，

又由（1）可知在Rt△PBC中，BC=8，PC=4，

∴PB=4，

∴EF=2，

即EF的长度不变．

第49题

下列函数中，不是反比例函数的是（　　）

A.y=

B.y=﹣（m不等于0）

C.y=

D.y=

参考答案：C

解析：

【考点】反比例函数的定义．

【分析】根据反比例函数的定义，反比例函数的一般式是（k≠0），即可判定各函数的类型是否符合题意．

【解答】解：A、符合反比例函数的定义，y是x的反比例函数，错误；

B、符合反比例函数的定义，y是x的反比例函数，错误；

C、y与x﹣1成正比例，y不是x的反比例函数，正确；

D、符合反比例函数的定义，y是x的反比例函数，错误．

故选C．

第50题

下列方程是一元二次方程的是（　　）

A.3x²+=0

B.2x﹣3y+1=0

C.（x﹣3）（x﹣2）=x²

D.（3x﹣1）（3x+1）=3

参考答案：D

解析：

【考点】一元二次方程的定义．

【分析】只含有一个未知数，且未知数的最高次数是2的整式方程叫做一元二次方程．一元二次方程有三个特点：（1）只含有一个未知数；（2）未知数的最高次数是2；（3）是整式方程．

【解答】解：A、3x²+=0是分式方程，故此选项错误；

B、2x﹣3y+1=0为二元一次方程，故此选项错误；

C、（x﹣3）（x﹣2）=x²是一元一次方程，故此选项错误；

D、（3x﹣1）（3x+1）=3是一元二次方程，故此选项正确．

故选D．

第51题

三角形两边的长分别是8和6，第三边的长是一元二次方程x²﹣16x+60=0的一个实数根，则该三角形的面积是（　　）

A.24

B.24或8

C.48或16

D.8

参考答案：B

解析：

【考点】解一元二次方程-因式分解法；勾股定理；勾股定理的逆定理．

【分析】由x²﹣16x+60=0，可利用因式分解法求得x的值，然后分别从x=6时，是等腰三角形；与x=10时，是直角三角形去分析求解即可求得答案．

【解答】解：∵x²﹣16x+60=0，

∴（x﹣6）（x﹣10）=0，

解得：x₁=6，x₂=10，

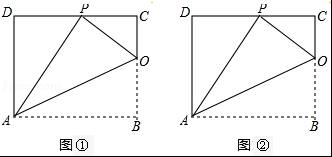
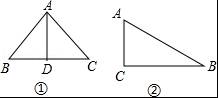
当x=6时，则三角形是等腰三角形，如图①，AB=AC=6，BC=8，AD是高，

∴BD=4，AD==2，

∴S_△ABC=BC•AD=×8×2=8；

当x=10时，如图②，AC=6，BC=8，AB=10，

∵AC²+BC²=AB²，

∴△ABC是直角三角形，∠C=90°，

S_△ABC=BC•AC=×8×6=24．

∴该三角形的面积是：24或8．

故选：B．

第52题

若，则等于（　　）

A.8

B.9

C.10

D.11

参考答案：C

解析：

【考点】比例的性质．

【分析】设=k，得出a=2k，b=3k，c=4k，代入求出即可．

【解答】解：设=k，

则a=2k，b=3k，c=4k，

即

=

=

=10，

故选C．

第53题

如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（　　）

A.∠B=∠C

B.∠ADC=∠AEB

C.BE=CD，AB=AC

D.AD：AC=AE：AB

参考答案：C

解析：

【考点】相似三角形的判定．

【分析】根据已知及相似三角形的判定方法进行分析，从而得到答案．

【解答】解：∵∠A=∠A

∴当∠B=∠C或∠ADC=∠AEB或AD：AC=AE：AB时，△ABE和△ACD相似．

故选C．

第54题

下列等式成立的是（　　）

A.sin 45°+cos45°=1

B.2tan30°=tan60°

C.2sin60°=tan45°

D.sin²30°=cos60°

参考答案：D

解析：

【考点】特殊角的三角函数值．

【分析】根据特殊角的三角函数值，分别计算即可判断．

【解答】解：A、因为sin45°+cos45°=+=．故错误．

B、因为2tan30°=，tan60°=，所以2tan30°≠tan60°，故错误．

C、因为2sin60°=，tan45°=1，所以2sin60°≠tan45°故错误，

D、因为sin²30°=， cos60°=，所以sin²30°=cos60°，故正确．

故选D．

第55题

在Rt△ABC中，∠C=90°，sinA=，则tanB的值为（　　）

A.

B.

C.

D.

参考答案：D

解析：

【考点】互余两角三角函数的关系．

【分析】根据题意作出直角△ABC，然后根据sinA=，设一条直角边BC为5x，斜边AB为13x，根据勾股定理求出另一条直角边AC的长度，然后根据三角函数的定义可求出tan∠B．

【解答】解：∵sinA=，

∴设BC=5x，AB=13x，

则AC==12x，

故tan∠B==．

故选：D．

第56题

把中考体检调查学生的身高作为样本，样本数据落在1.6～2.0（单位：米）之间的频率为0.28，于是可估计2 000名体检中学生中，身高在1.6～2.0米之间的学生有（　　）

A.56

B.560

C.80

D.150

参考答案：B

解析：

【考点】用样本估计总体；频数与频率．

【分析】根据频率的意义，每组的频率=该组的频数：样本容量，即频数=频率×样本容量．数据落在1.6～2.0（单位：米）之间的频率为0.28，于是2 000名体检中学生中，身高在1.6～2.0米之间的学生数即可求解．

【解答】解：0.28×2000=560．故选B．

第57题

为了解自己家的用电情况，李明在6月初连续几天同一时刻观察电表显示的情况记录如下：

A.105千瓦时

B.115千瓦时

C.120千瓦时

D.95千瓦时

参考答案：C

解析：

【考点】用样本估计总体．

【分析】根据样本估计总体的统计思想：可先求出7天中用电量的平均数，作为6月份用电量的平均数，则一个月的用电总量即可求得．

【解答】解：30×=120（千瓦时）．

故选C．

第58题

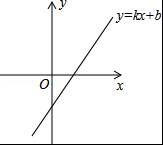
已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是（　　）

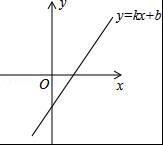
A.

B.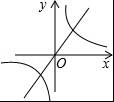

C.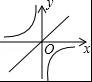

D.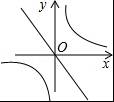

参考答案：C

解析：

【考点】反比例函数的图象；一次函数的图象；一次函数图象与系数的关系．

【分析】根据一次函数图象可以确定k、b的符号，根据k、b的符号来判定正比例函数y=kx和反比例函数y=图象所在的象限．

【解答】解：如图所示，∵一次函数y=kx+b的图象经过第一、三、四象限，∴k＞0，b＜0．

∴正比例函数y=kx的图象经过第一、三象限，

反比例函数y=的图象经过第二、四象限．

综上所述，符合条件的图象是C选项．

故选：C．

第59题

点P（2m﹣3，1）在反比例函数的图象上，则m=　　．

参考答案：2

解析：

【考点】反比例函数图象上点的坐标特征．

【分析】此题可以直接将P（2m﹣3，1）代入反比例函数解析式即可求得m的值．

【解答】解：∵点P（2m﹣3，1）在反比例函数的图象上，∴（2m﹣3）×1=1，解得m=2．

故答案为：2．

第60题

已知一个函数的图象与y=的图象关于y轴成轴对称，则该函数的解析式为　　．

参考答案：y=﹣

解析：

【考点】反比例函数的性质．

【分析】根据图象关于y轴对称，可得出所求的函数解析式．

【解答】解：关于y轴对称，横坐标互为相反数，纵坐标相等，

即y=，

∴y=﹣

故答案为：y=﹣．