九年级（上）期末数学试卷集（328题）

---

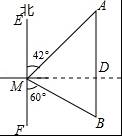
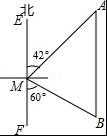
如图，一艘渔船位于小岛M的北偏东42°方向、距离小岛180海里的A处，渔船从A处沿正南方向航行一段距离后，到达位于小岛南偏东60°方向的B处．

（1）求渔船从A到B的航行过程中与小岛M之间的最小距离（参考数据：参考数据：sin42°≈0.6691，cos42°≈0.7431，tan42°≈0.9044，≈1.732，结果精确到0.1海里）

（2）若渔船以20海里/小时的速度从B沿BM方向行驶，求渔船从B到达小岛M的航行时间（结果精确到0.1小时）

知识点：试卷02

参考答案：见解析

解析：

【考点】解直角三角形的应用-方向角问题．

【分析】（1）过点M作MD⊥AB于点D，根据∠AME的度数求出∠A=42°，再根据AM的值求出和特殊角的三角函数值即可求出答案；

（2）在Rt△DMB中，根据∠BMF=60°，得出∠DMB=30°，再根据MD的值求出MB的值，最后根据路程÷速度=时间，即可得出答案．

【解答】解：（1）过点M作MD⊥AB于点D，

∵∠AME=42°，

∴∠A=42°，

∵AM=180海里，

∴MD=AM•sin42°≈120.4（海里），

答：渔船从A到B的航行过程中与小岛M之间的最小距离约为120.4海里；

 

（2）在Rt△DMB中，

∵∠BMF=60°，

∴∠DMB=30°，

∵MD=120.4海里，

∴MB=≈139，0，

∴139.0÷20≈7.0（小时），

答：渔船从B到达小岛M的航行时间约为7.0小时．